はじめに
文章にいくつかの特定ワードが含まれているかの判定を考えます。例えば、「特定ワードを含むツイートすると応募できるキャンペーン」でしょうか。もしくは「ニコニコ大百科1の自動リンクを実装する」だとイメージしやすいかもしれません。
茶番 (ガード節)
早速ですが、これはどうやって判定しましょうか。
- あほこらかな?と思った方
- -> あほこら法2を使う記事なので、ご存じならこの記事は不要かもしれません
- 正規表現かな?と思った方
- -> 次にお進みください
(茶番ありがとうございました)
というわけで エイホ - コラシック法 を紹介します
上に書いた問題はエイホ - コラシック法を使うとさらに効率的に判定できます。エイホ - コラシック法は、文字列に特定のワードが含まれているかを判定するアルゴリズムです。ちなみに英語で書くと Aho-Corasick です2。
同じ問題は正規表現を使うと解決できそうですが、計算量に差があるので比較してみます。
ちなみに、通常文字のみを使ったマッチングに有効です。
[a-z]{3,8} や .+\.csv のような、通常文字を使わないマッチングはエイホ - コラシック法ではできません。
計算量の比較
正規表現
まずは正規表現から。
正規表現の計算量を正確に出すのは難しいのですが、文字列の長さを $S$ として、最低でも $O(S)$ かかることはわかります。何もマッチしなかった時は $S$ 文字を判定するからですね。これが特定ワードの個数だけ判定されるので、ワードの個数を $N$ とすると、全体では $O(S * N)$ の計算量になりました。
https://regex101.com/#pcre で試してみると、だいたい $N * S$ のステップ数になりました。
(文字数が 10 の文字列に対してマッチしない 3 ワードを実行すると 33 ステップでした)
マッチするワードがあるときは全体の合計ステップ数が減りました。
計算量の考察は最大ステップ数を使うのが一般のため、今回はマッチしない条件で考えます。
エイホ - コラシック法
続いて、エイホ - コラシック法の計算量です。
エイホ - コラシック法は正規表現に比べると複雑で、実際のステップ数を出すのは難しいので、計算量のオーダーだけを書きますね。
文字列の長さを $S$ として、全特定ワードの長さの和を $W$ とすると、エイホ - コラシック法の計算量は $O(S + W)$ になります。
計算量のまとめ
- 正規表現の計算量は $O(S * N)$ ($S$ は文字列の長さ、$N$ はワードの個数)
- エイホ - コラシック法の計算量は $O(S + W)$ ($S$ は文字列の長さ、$W$ はワードの長さの和)
となりました。
規模が大きいほど差がわかりやすいので、ニコニコ大百科の例で考えてみましょう。
文字列 (記事) の長さは $S$ = 5000程度にします。
辞書の単語数は詳しくわかりませんが、$N$ = 5000程度でしょうか。辞書で有名な広辞苑は25万語というので、もっと多いかもしれませんね。
ワードの長さの和は $W$ = 25000 程度でしょうか。平均5文字とします。
このとき、正規表現のステップ数の概算は $S * N = 5,000 * 5,000 = 25,000,000$ になります。
これに対して、エイホ - コラシック法は $S + W = 30,000$ です。
実際は定数倍があるので正確なステップ数はわかりませんが、多くても100倍程度です。ステップ数に大きな違いがあることがわかります。
文字列の長さやワードの個数が増えるたびにステップ数の差は開いていきます。規模が大きくなるほど、エイホ - コラシック法の効率の良さが光ります。
エイホ - コラシック法ってなにしてるの?
さて、エイホ - コラシック法の実装ですが、詳しく書くと長くなる & このページ がわかりやすい ので、リンク先をご覧ください(すみません)。
簡単に書くと、辞書の単語から特定のデータ構造を構築します。そのあと、文字列を1文字ずつ確認するアルゴリズムです。このときのデータ構造は、トライ木の各ノードに、対応する別ノードへのリンクを貼ったものを使います。
データ構造の構築に $O(W)$ かかり、文字列の確認に $O(S)$ かかるので、全体では $O(W + S)$ という計算量です。
使ってみる
Rust に aho_corasick クレート があるので使ってみます3。
use aho_corasick::AhoCorasick;
fn main(){
let patterns = &["apple", "maple", "Snapple"];
let haystack = "Nobody likes maple in their apple flavored Snapple.";
let ac = AhoCorasick::new(patterns);
let mut matches = vec![];
for mat in ac.find_iter(haystack) {
matches.push((mat.pattern(), mat.start(), mat.end()));
}
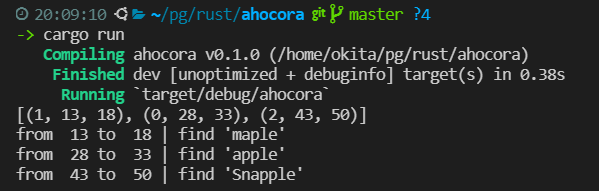
println!("{:?}", matches);
for (pos, start, end) in matches.iter() {
println!("from {:>3} to {:>3} | find '{}'", start, end, patterns[*pos]);
}
}
さいごに
エイホ - コラシック法は高速で効率的ですが、使うにはアルゴリズムへの理解が必要です。
冒頭に書いたツイートの例のように、文字数が少ないものを対象にする際は正規表現での判定も現実的な選択肢になります。
用法・容量を守って楽しいアルゴリズムライフをお過ごしください。
※追記
ここまで書いてなんなのですが、どうやら a|b|c のような正規表現は中でエイホ-コラシック法が使われているみたいです。なので、わざわざエイホ-コラシック法を使わなくても要件を満たせる機会がたくさんありそうです。
おまけ
趣味でトライ木を書いたことがあるので貼っておきます。
アルファベット26文字に対応しています。
trie-rust.rs (165行)
use itertools::Itertools;
use std::collections::VecDeque;
use std::str;
#[derive(Debug)]
struct Node {
prefix: String,
is_leaf: bool,
children: Vec<usize>,
}
impl Node {
pub fn new() -> Node {
Node {
prefix: String::from("-"),
is_leaf: false,
children: vec![],
}
}
pub fn from(c: &str) -> Node {
std::assert_eq!(c.len(), 1, "arg is {}", c);
let mut node = Node::new();
node.prefix = String::from(c);
node
}
}
pub struct Trie {
nodes: Vec<Node>,
}
impl Trie {
pub fn new() -> Trie {
Trie {
nodes: vec![Node {
prefix: String::from("-"),
is_leaf: false,
children: vec![],
}],
}
}
pub fn insert(&mut self, s: &str) {
std::assert!(s.len() > 0, "insert size <= 0");
self.insert_dfs(s, 0);
}
fn insert_dfs(&mut self, s: &str, idx: usize) {
// 入力文字の先頭を見る
// マッチすれば次の文字を見る
// マッチしなければ追加する
for &i in &self.nodes[idx].children {
// みつかった
if &self.nodes[i as usize].prefix == &s[0..1] {
let child_idx: usize = i;
self.insert_dfs(&s[1..], child_idx);
return;
}
}
// みつからなかった
let mut next: Node = Node::from(&s[0..1]);
next.is_leaf = s.len() == 1;
let next_idx: usize = self.nodes.len();
let _ = &self.nodes.push(next);
let _ = &self.nodes[idx].children.push(next_idx);
if s.len() > 1 {
self.insert_dfs(&s[1..], next_idx);
}
}
pub fn remove(&mut self, s: &str) {
self.remove_dfs(s, 0);
}
fn remove_dfs(&mut self, s: &str, idx: usize) -> bool {
if s.len() == 0 {
if self.nodes[idx].is_leaf && self.nodes[idx].children.len() == 0 {
self.nodes[idx].prefix = String::from("non");
return true;
}
self.nodes[idx].is_leaf = false;
return false;
}
for &i in &self.nodes[idx].children {
// みつかった
if &self.nodes[i as usize].prefix == &s[0..1] {
let child_idx: usize = i;
if self.remove_dfs(&s[1..], child_idx) && self.nodes[idx].children.len() == 1 {
self.nodes[idx].is_leaf = false;
self.nodes[idx].prefix = String::from("non");
return true;
}
return false;
}
}
false
}
pub fn exist(&self, s: &str) -> bool {
self.exist_dfs(s, 0)
}
fn exist_dfs(&self, s: &str, idx: usize) -> bool {
if s.len() == 0 {
return self.nodes[idx].is_leaf;
}
for i in &self.nodes[idx].children {
// みつかった
if &self.nodes[*i as usize].prefix == &s[0..1] {
return self.exist_dfs(&s[1..], *i);
}
}
false
}
pub fn predict(&self, s: &str) -> Vec<String> {
self.predict_impl(s, 0)
.iter()
.map(|suffix| String::from(s) + suffix)
.collect_vec()
}
fn predict_impl(&self, s: &str, idx: usize) -> Vec<String> {
if s.len() == 0 {
// ここでBFS をする
let mut ret: Vec<String> = vec![];
let mut q = VecDeque::new();
for &i in &self.nodes[idx].children {
let qi = i;
q.push_back((qi, String::new()));
}
while let Some(front) = q.pop_front() {
let (idx, s) = front;
if &self.nodes[idx].prefix == "non" {
continue;
}
let now = String::from(s) + &self.nodes[idx].prefix;
if self.nodes[idx].is_leaf {
ret.push(now.clone());
}
for &i in &self.nodes[idx].children {
let qi = i;
q.push_back((qi, now.clone()));
}
}
return ret;
}
for &i in &self.nodes[idx].children {
if &self.nodes[i].prefix == &s[0..1] {
let child_idx = i;
return self.predict_impl(&s[1..], child_idx);
}
}
vec![]
}
}