DAG（有向非巡回グラフ）の紹介とトポロジカルソート

はじめに

DAG はご存じでしょうか。Directed Acyclic Graphの略で、日本語だと有向非巡回グラフといいます。
グラフとあるように、グラフ理論の用語です。wiki はこちら：有向非巡回グラフ
最近は Airflow で使われていて、それをきっかけに知った方もいるのではないでしょうか。
この記事では、そんな DAG を紹介してみます。

前提知識

次のグラフ理論の用語を知っていること

• ノード・節点・頂点
• エッジ・枝・辺
• 有向グラフ

---

前提知識にあるグラフ理論についてすこしだけ説明してみます。知っている方は読み飛ばしてください。wikiはこちら：グラフ理論
まず、グラフについて。グラフとは、物事を「点」と「線」で表したものです。具体例を以下に挙げてみます。

• 路線図の駅を点、線路を線にするとグラフになります。こんなイメージです。
  • https://imidas.jp/genre/detail/K-127-0145.html
  • https://www.cresco.co.jp/blog/entry/7125/
  • https://qiita.com/keiono/items/29286f49b15a5b13c987
• 地図の都市を点、道を線とすることでグラフになります。
  • https://www.ajimatics.com/entry/2018/01/30/133238
• 通信ネットワークもグラフになります。サーバーやルーター、PCを点として、通信路を線とすればグラフになります。
  • それっぽい例がみつかりませんでした ><
  • Google画像検索「通信ネットワーク」
• SNS のアカウントを点、フォロー / フォロワーの関係を線にすることでグラフになります。
  • これもそれっぽい例が見つかりませんでした ><

さて、グラフを軽く紹介しましたが、グラフの性質に注目した理論体系のことをグラフ理論といいます。「理論」とつくとかっこいいですね。
グラフ理論を使うと、地図や通信ネットワークの最短経路を見つけたり、マッチングアプリで効率的なマッチングをしたり、効率的な作業の手順書をつくったりできます。

(作業の手順書についてはこのあとで紹介するので楽しみにしていてください)

ここで、用語に書いた「ノード・節点・頂点」は点のことです。また、「エッジ・枝・辺」は線のことです。

また、有向グラフについて。有向グラフとは、辺に向きのあるグラフのことです。だから「有向」と書くんですね。
上で例に出した SNS は有向グラフになります。というのも、SNS　はフォローしている人とされている人とで向きがありますね。相互フォローの場合は双方向ですし、そうでない場合は一方向の辺ができます。このように、辺に向きのあるグラフのことを有向グラフといいます¹。

DAG の紹介

本編です。

「はじめに」でも書きましたが、 DAG とは「有向非巡回グラフ」のことです。この用語は３つに分かれていて、「有向・非巡回・グラフ」に分けられます。
「有向」とは、有向グラフのことですね。
「非巡回」とは、グラフにループ・閉路がないということです。つまり、有向辺に沿って頂点を移動したときに、元に戻ってくるような経路がありません。
「グラフ」はそのまま、グラフ理論のグラフのことです。

まとめると、DAG とは「閉路のない有向グラフ」と言えます。

DAG の特徴

さて、わざわざ名前がついているくらいなので、DAG だと嬉しいことがあるのでしょう。それを紹介します。といっても、ここでは以下のトポロジカルソートだけを紹介します。

トポロジカルソート

DAG だとトポロジカルソートができます。トポロジカルソートをすると、すべての有向辺が同じ方向を向きます。

といってもピンときませんね。具体例を書いてみます。

このような有向グラフがありあます。(でこぼこしていますが、左から [1,2,3,4] と並べたつもりです)

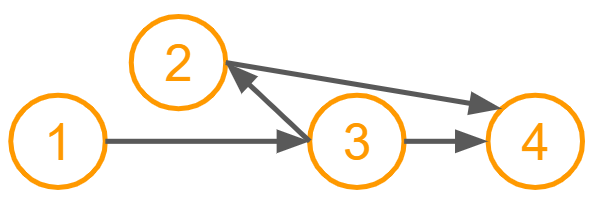
トポロジカルソートをすると下のようになります。

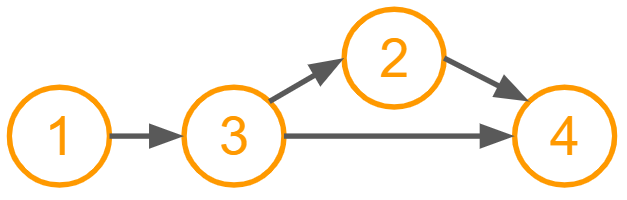
この例ではトポロジカルソートにより、 [1,2,3,4] という列が [1,3,2,4] にソートされました。注目する点を書いてみます。

• 順番は変わりましたが、頂点と辺の関係は変わっていません。
• 全ての辺の向きが 左→右 になっています

というものがトポロジカルソートでした。単純ですね。

トポロジカルソートには注意点があります。数値や文字列などのソートとは違って、結果が一意に決まらない²ことがあります。 たとえば、以下の有向グラフをトポロジカルソートすると、

下のように、[1,3,2] と [3,1,2] の 2通りのソート結果がありえます。

注意です。

※トポロジカルソートの実装例はありません。すみません。各頂点の入次数に着目してガチャガチャする³とできます。
頂点の数を $V$、辺の数を $E$ として、$O(V + E)$ の計算量で実装できます。

トポロジカルソートの利点

さて、トポロジカルソートの概要を説明しました。続いて利点を紹介します。ここでは２つ紹介します。

閉路検出

トポロジカルソートをすることで、有向グラフ上に閉路があるかどうかを検出できます。ですが、閉路検出はDFS (Depth First Search : 深さ優先探索) などでも実現できるので、特殊性はありません。

(さらっと終わらせます)

視覚的に理解しやすくなる

トポロジカルソートをすることで、視覚的に理解しやすくなります。

例えば、グラフを可視化することもあるかと思いますが、頂点や辺が増えるにつれて構造を理解しにくくなります。そんな時にトポロジカルソートされていると、見やすくなることがあります。

具体例として作業の手順書をつくります。私はそうめんが好きなので、そうめんを茹でる手順書をつくってみます。

まずは思いつく作業を列挙します。

作業には依存関係があるので、 矢印をつけます。(茹でる前に冷やしたりはできない、、という類の依存関係です)

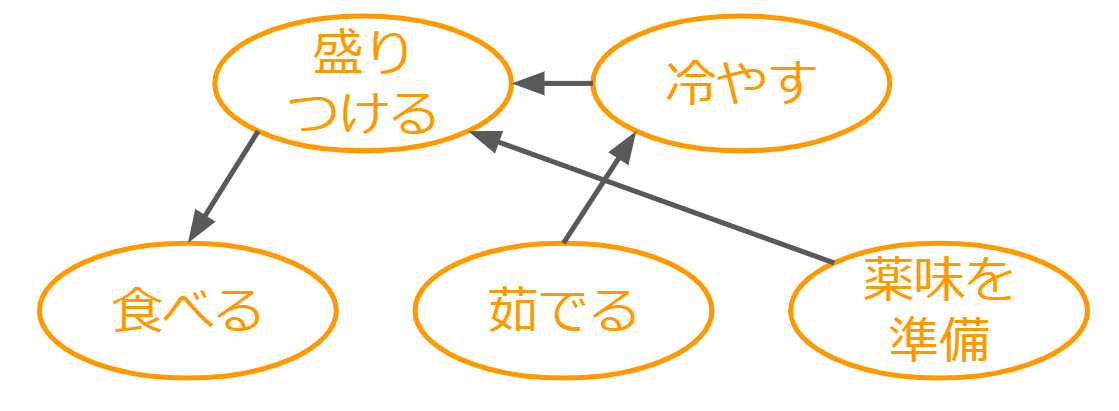
あとはトポロジカルソートをします。

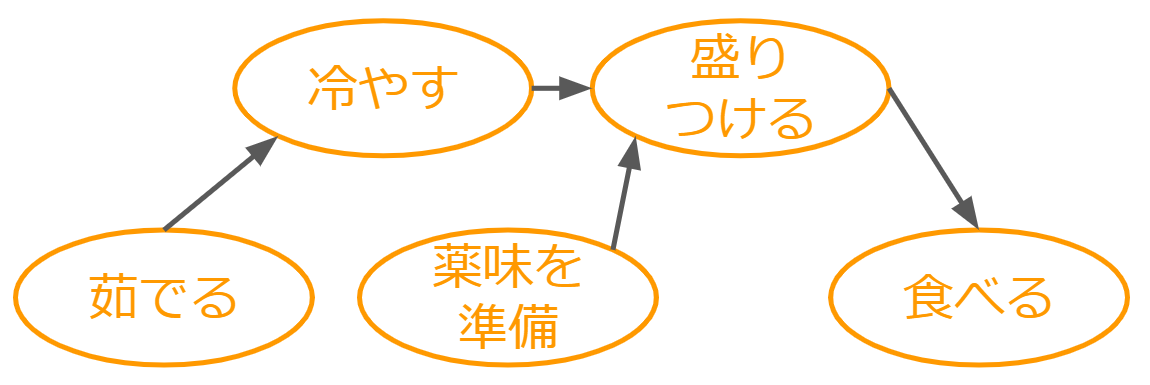
なんということでしょう。あんなに複雑そうに見えたそうめんを茹でる手順が、こんなにシンプルになりました。この手順書によると、「薬味を準備」は「茹でる」や「冷やす」の合間にやればいいことがわかります。

トポロジカルソートをする前と後、どちらがわかりやすいかは一目瞭然ですね。このように、トポロジカルソートをすると視覚的に理解しやすくなります。

弊社ではフロントエンドのページをコンポーネントに分割するときに、トポロジカルソートを利用して作業手順書を書いています。jsonでお手軽に編集できて、かなり便利です。(PRだと...!?)
コチラです↓↓ つかってみてね。

おまけ (強連結成分分解)

ループがあるときにもトポロジカルソートっぽいことをしたいことありませんか？私はあります。

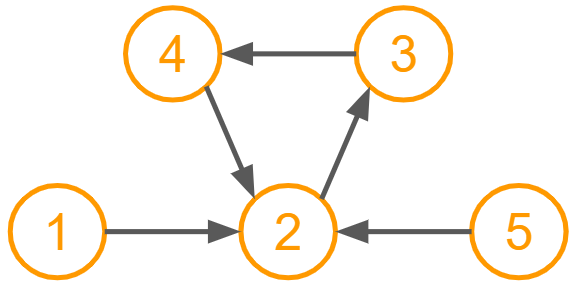
ループを無視すればトポロジカルソートができますよね。
こういうときには「強連結成分分解」をします。名前の通り、「強連結成分」に分解することです。
「強連結成分 (SCC: Strongly Connected Component)」とは、お互いに行き来できる頂点の最大集合です。
閉路とSCCは概念的にとても近いです (閉路は列でSCCは集合なので、同じではないです)。
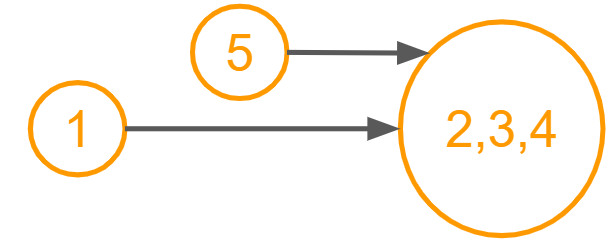
有向グラフでは強連結成分に分解して、強連結成分をひとつの頂点とすることで、DAG とみなすことができます。

例えば、閉路 [2,3,4] がある有向グラフのとき

閉路 [2,3,4] をひとつのノードとみなすとDAGになるので、

トポロジカルソートができます。

実装例はありません。すみません。辺を逆向きに張ったグラフを用意して、順方向と逆方向でそれぞれDFSをやると求まります。
頂点の数を $V$、辺の数を $E$ として、$O(V + E)$ の計算量で実装できます。

1. 路線図をグラフとしてみた時にも辺の向きがありますが、(一部の例外を除いて)すべての路線が双方向なので、有向グラフの例としてあまりいい例じゃないと思って紹介しませんでした。すべての辺が双方向の有向グラフは、辺の向きがない無向グラフと変わりません。 ↩

2. 通常は実装時に Queue を使いますが、PriorityQueue を使うことで一意の結果にすることもできます。利用例 (AtCoderの問題に飛びます) ↩

3. DFS で帰りがけ順にホイホイする方法もあります。 ↩