「14日で作る量子コンピュータ」を読んでみる。3日目

はじめに

　今回は重ね合わせの原理と、電子波束についてまとめる。

3 電子波束の観察

重ね合わせの原理

　重ね合わせの原理は、シュレディンガー方程式を満たす複数の解を、足し合わせてできる関数もまたシュレディンガー方程式の解となっていると言う原理です。例えば以下のようなある分布にしたがって、$\psi_k$を重ね合わせた波動関数を用意する。

$$
\psi(x,t)=\int_{-\infty}^{\infty}a(k)\varphi_k(x)e^{-i\omega(k)t}dk=\int_{-\infty}^{\infty}a(k)e^{ikx-i\omega(k)t}dk
$$

　これをシュレディンガー方程式に代入してみる、この時自由空間なのでポテンシャルは0したがって

$$
i\hbar\frac{\partial}{\partial t}\int_{-\infty}^{\infty}a(k) e^{ikx-i\omega(k)t}dk=\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}\int_{-\infty}^{\infty}a(k)e^{ikx-i\omega(k)t}dk
$$

$$
\int_{-\infty}^{\infty}a(k)\hbar \omega(k) e^{ikx-i\omega(k)t}dk=\int_{-\infty}^{\infty}a(k)\frac{\hbar^2k^2}{2m}e^{ikx-i\omega(k)t}dk
$$

$$
\int_{-\infty}^{\infty}a(k)\left[\hbar \omega(k)-\frac{\hbar^2 k^2}{2m}\right] e^{ikx-i\omega(k)t}dk=0
$$

全ての位置と時間にかかわらず左辺はゼロになる時重ね合わせの原理は成り立つことになるので、括弧の中身がゼロになる条件について調べると

$$
\omega(k)=\frac{\hbar k^2}{2m}
$$

これは$\omega$自体の定義と同じなので、常に成り立つ。つまり常に重ね合わせの原理が成り立つことが示された。

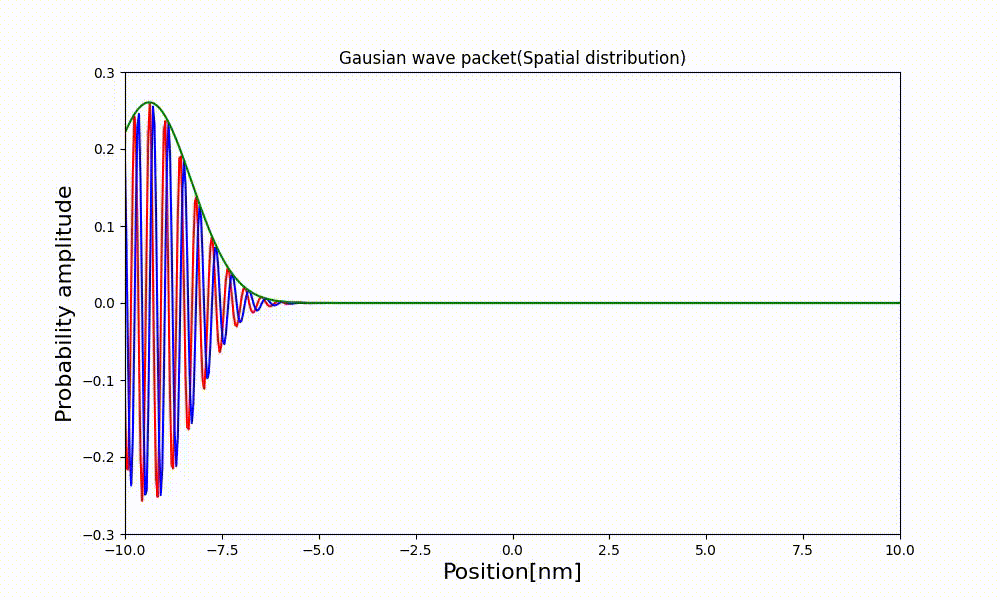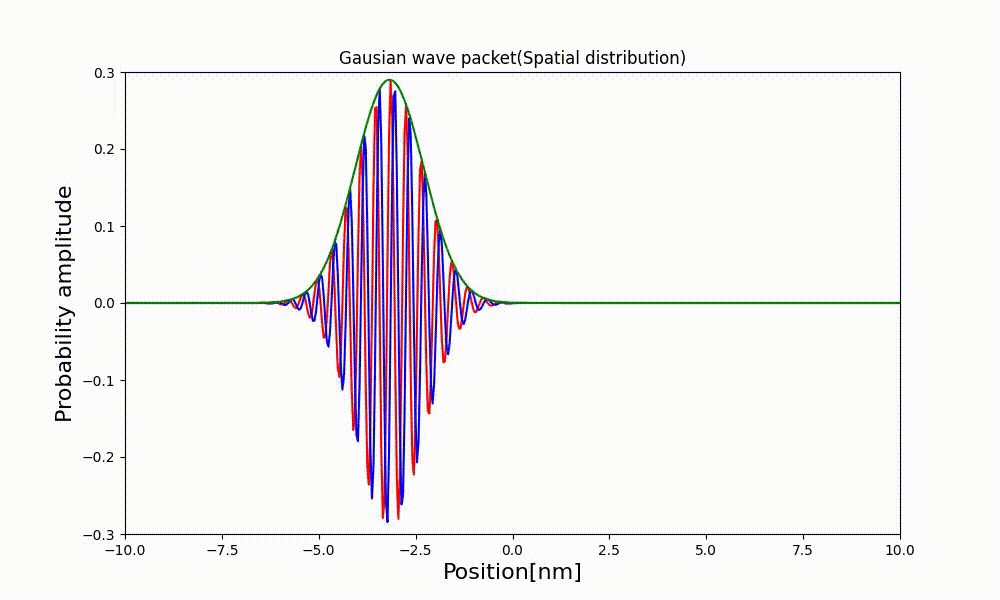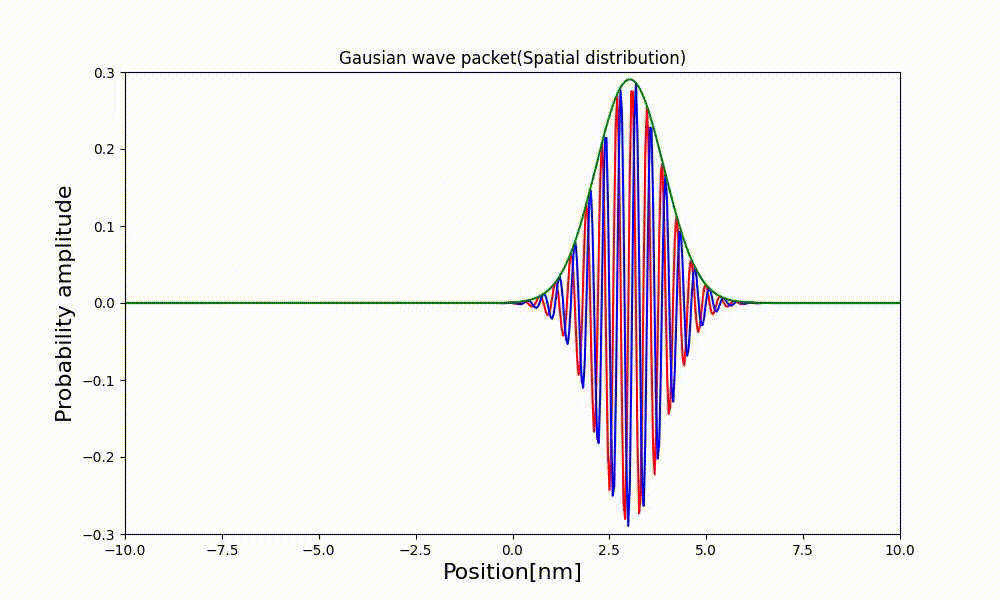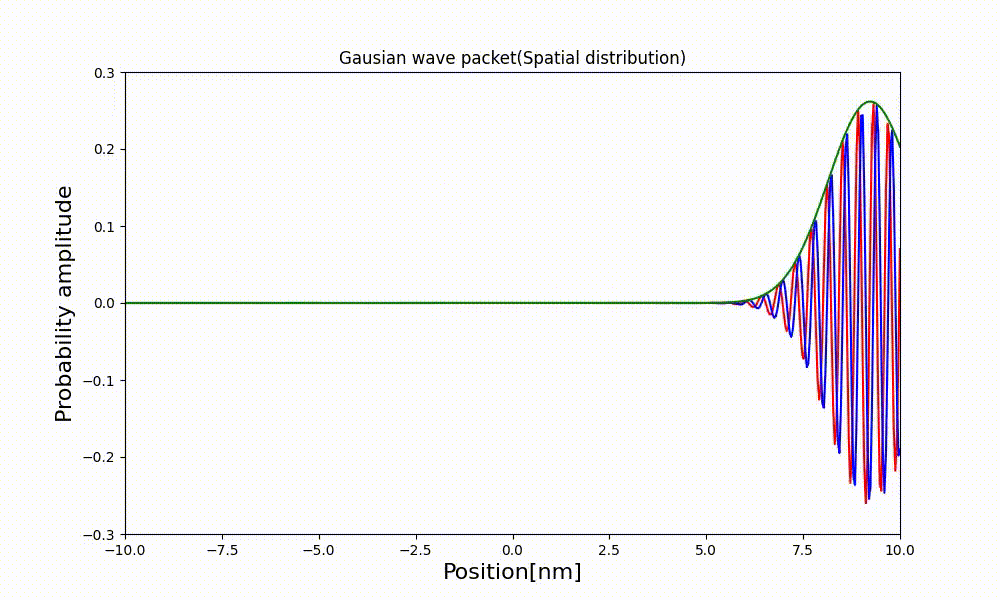
3.2 電子波束の観察

　$a(k)$はどのような分布でも良いので、適当な定数$k_0$を中心とするガウス分布とするとa(k)は

$$
a(k)=e^{-(\frac{k-k_0}{2\sigma})^2}
$$

　この時の波動関数をプロットしてみる。

3.2.1 定数

　ここで新たに必要となる定数は

# 空間の分割数
NX = 500
# 空間分割サイズ
dx = 1.0e-9
# 計算区間
x_min = -10.0 * dx
x_max = 10.0 * dx
# 重ね合わせる数
NK = 200
# kの偏差
sigma = math.sqrt(math.log(2.0)) * 1.0e9
# kの分割
dk = 20.0 / NK
# 波束の中心エネルギー
E0 = 10.0 * eV
# 波束の中心
k0 = math.sqrt(2.0 * me * E0 / hbar ** 2)
omega0 = hbar / (2.0 * me) * k0 ** 2
# 計算時間の幅
ts = -50
te = 50
# 時間間隔
dt = 1.0e-16
# 虚数単位
I = 1.0j

3.2.2 関数の定義

　プロットを作るに当たって必要なのは、ある時点tにおけるグラフの配列を出力する関数が必要なので、

def dist_t(xl, t):
    psi_real = []
    psi_imag = []
    psi_abs = []
    for x in xl:
        # スケーリング
        psi_c = psi(x, t) * dx * dk / 10.0
        psi_real.append(psi_c.real)
        psi_imag.append(psi_c.imag)
        psi_abs.append(abs(psi_c))
    return psi_real, psi_imag, psi_abs

　そして、(x,t)が与えられた時の確率分布を出力する関数psiを定義する。

def psi(x, t):
    psi_sum = 0.0 + 0.0j
    for kn in range(NK):
        # 定数を取得
        k = k0 + dk * (kn - NK/2)
        omega = hbar / (2.0 * me) * k ** 2
        # 重ね合わせ
        psi_sum += cmath.exp(I * (k * x - omega * t)) * cmath.exp(-((k - k0) / (2.0 * sigma)) ** 2)
    return psi_sum

3.2.3 アニメーションのプロット

　これらを用いてプロットを行う。

xl = np.linspace(x_min, x_max, NX)
# アニメーション作成用の配列
ims = []
fig1 = plt.figure(figsize=(10, 6))

for t in range(ts, te + 1):
    t_real = t * dt
    psi_real, psi_imag, psi_abs = dist_t(xl * dx, t)
    # コマの描写
    img = plt.plot(xl, psi_real, 'red')
    img += plt.plot(xl, psi_imag, 'green')
    img += plt.plot(xl, psi_abs, 'blue')
    # コマの追加
    ims.append(img)

# グラフの描画
plt.title("Gaussian wave packet(Spatial distribution)")
plt.xlabel("Position[nm]", fontsize=16)
plt.ylabel("Probability amplitude", fontsize=16)
# 描画範囲
plt.xlim([-10.0, 10.0])
plt.ylim([-0.3, 0.3])
# アニメーション生成
ani = animation.ArtistAnimation(fig1, ims, fontsize=16)
ani.save("g_wave_packet.html", writer=animation.HTMLWriter())

plt.show()

3.3 出来上がったアニメーション

　↓が出来上がった動画。時間が立つほど分布の幅が広がっているのが観察できる。