初めに
最近p5.jsというものを知りまして、インタラクティブにGUIを操作できるものが簡単に作れるのが楽しくて色々作ってました。それで何かしら物理現象をシミュレーションしようと思い立ちまして、重力によって光が曲がる様子を描画してみることにしました。
厳密に再現するのは能力的にも計算量的にも難しそうなので今回は位置の補正のみ行います。
重力レンズの仕組み
重力レンズは銀河などの重力によって後方にある星の光などが曲がることで実際とは異なる見え方をする現象です。
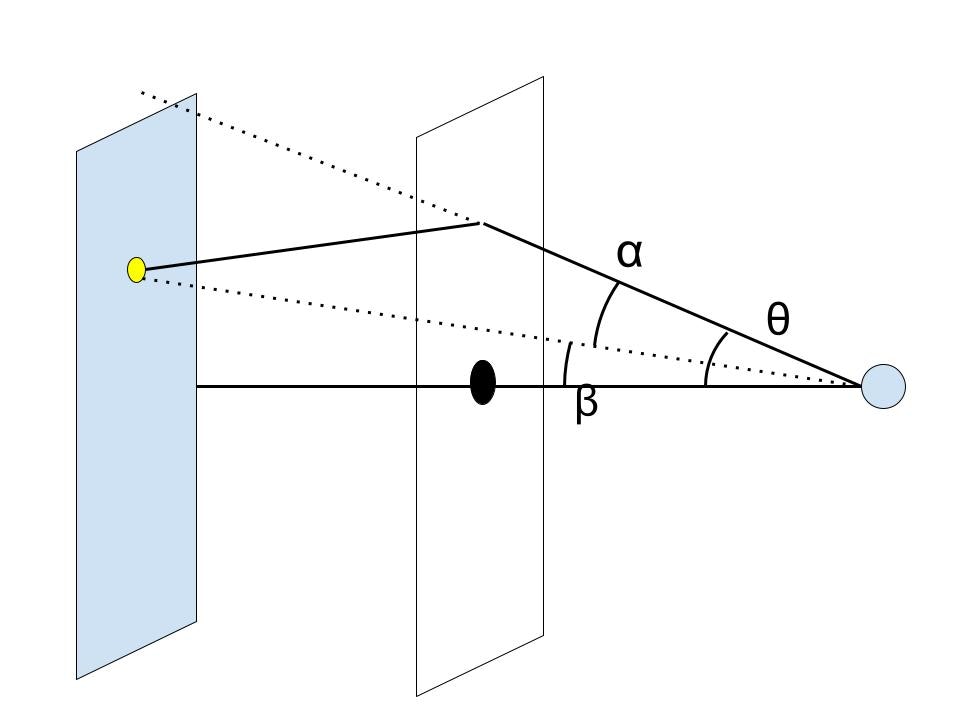
重力によって歪められた光の角度には以下の関係が成り立ちます
\beta = \theta - \alpha(\theta)
今回はレンズに使う重力は質点のように一つの点から重力が発生している様子を想定しているので$\alpha$は以下の式によって表されます
\alpha = \frac{C(r - r')}{|r - r'|^2} \quad (Cは適当な定数)
ここで$\theta$が十分小さければ$r-r'= $ $\vec\theta$とみなせるのでここで$\vec\beta$と$\vec\theta$について重力の中心を原点とすればこの二つは平行なので、この方向の単位ベクトル$\vec e$に対して
\vec\beta = \beta \vec e\\
\vec\theta = \theta \vec e
とすると
\alpha(\theta) = \frac{C}{\theta}
したがって$\beta$は
\beta = \theta + \frac{C}{\theta}
通常観測できるのは$\theta$であり実際の位置$\beta$を出力するためこの式を使って$\beta(\theta)$の関数として使用するだけですむが、今回は$\beta\rightarrow\theta$を行いたいので、この式を$\theta$について解いて
\theta = \frac{\beta±\sqrt{\beta+4C}}{2}
これを用いて描画していく
p5.jsでの描画
これを実装したのがこちらです。p5jsのCollectionsです。見れなかったら教えてください
https://editor.p5js.org/aokyut/collections/U5-u0xfNh
使い方はキャンバス上でクリックだけです。そうすると重力が発生しその影響で線や点の位置が歪むのが確認できると思います。ぜひ遊んでみてください
最後に
今回は重力レンズによる光の屈折を描画しました。本当であれば位置だけでなく光の形が変化する様子も再現したかったのですが難しいので諦めました。pythonの方で再現するのもありだと思います。他にもp5.jsで色々作っているのですがそちらも公開しようか悩んでいます。