はじめに
新型コロナウイルス感染症(COVID-19)の感染者数は、中国から世界中に広がり、2020年3月14日現在、感染者145,637名、死者5,436名と大変な数に上っています。しかし、日本の状況をみると、感染者数は734名と、韓国の8086名の9.1%、イタリアの17,660名の4.2%に留まっています。
この明らかな差の理由として指摘されているのが、日本はPCR検査数を絞っているのではないか?という説です。そのため、実際にどれくらい絞っているのか?絞ることの意義は何か?他国は検査しすぎて医療崩壊しているではないか?、など議論を巻き起こしています。
しかし、あまり定量的な議論がなされていないために、テレビやネット等を通じたアバウトな感情論が展開され、正しい理解の妨げになっているように思われます。そこで、本記事では、ベイズの定理に基づいて、PCR検査を絞る意義に焦点を当てて検討してみました。
PCR検査とは?
まず、PCR(Polymerase Chain Reaction)検査とは何なのかをざっくり見てみましょう。国立感染研究所のマニュアルやタカラバイオのPCR検査の手引きなどを参考にしながら、概要を図示すると次のような検査のイメージです。
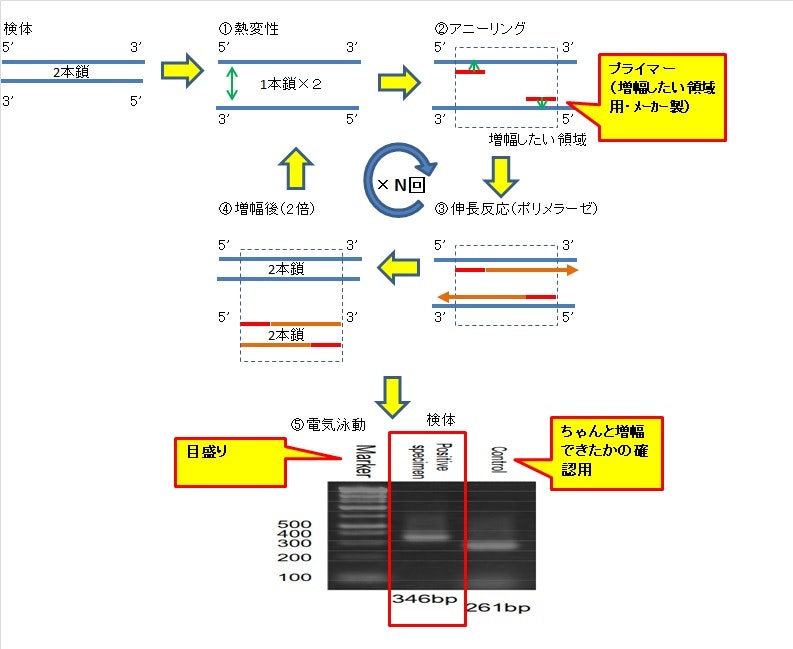
要するに、DNAの2本鎖を分解し、特定部位を増幅し、を繰り返しながら、ウイルスの特徴的な領域を増やして、その部分が電気泳動で目視できれば、陽性ということのようです。本当にウイルスに特徴的な部分だけを十分に増幅(2^N倍)できれば、高い精度(精度については後で議論)で検出できるようですね。
ただし、以下のような要因で検出精度が落ちることがあるようです。
- 熱変性の段階で、DNAが十分に分離しない。
- アニーリングの段階で、プライマーが誤って結合する。
- 伸長の段階で、DNAポリメラーゼの働きが悪くなる。
- 副産物が生成する。
検査の感度・特異度
検査に関連してよく耳にする言葉として、感度や特異度がありますが、関連する用語を整理しておきましょう。こちらのWikiがよくまとまっています。
- 感度(sensitivity または再現率 recall): 罹患している場合に陽性となる割合
- 特異度(specificity): 罹患していない場合に陰性となる割合
- 適合率(precision): 陽性の中で罹患している割合
- 正解率(accuracy): 全体の中で罹患して陽性、罹患していなくて陰性の割合
COVID-19(SARS-CoV-2)のPCR検査に関しては、諸説ありますが、感度は70%程度、特異度は90%以上との報告があるようです。ただし、感度は検体の取り方(咽頭などを綿棒で拭う)や輸送環境などの影響を受けたり、特異度はPCR検査のプロセスに影響を受ける可能性があり、確固とした数値にはならないでしょう。実際には、人体の全てにウイルスが1個もいないのか検査することなど物理的に不可能なので、感度・特異度の真値なるものはないのでしょう。
さて、上記の感度・特異度の定義を見ると、事後確率や同時確率のことを言っているのと思われた方も多いと思います。なので、改めて数式で定義してみましょう。
\begin{eqnarray}
感 度:RC &=& P(検査=T|罹患=T) \\
特異度:SP &=& P(検査=F|罹患=F) \\
適合率:PC &=& P(罹患=T|検査=T) \\
正解率:AC &=& P(検査=T,罹患=T) + P(検査=F,罹患=F)\\
\end{eqnarray}
また、よく耳にする言葉として、偽陽性、偽陰性がありますが、これらは以下のように定義されます。
\begin{eqnarray}
偽陽性率:FP &=& P(検査=T|罹患=F) = 1 - 特異度 \\
偽陰性率:FN &=& P(検査=F|罹患=T) = 1 - 感度
\end{eqnarray}
ベイズの定理
ベイズの定理は事前確率と事後確率の関係を表す公式です。機械学習界隈でも、ベイズ推定などでよく出てきますね。
P(B|A)=\frac{P(A|B)P(B)}{P(A)}
さて、ベイズの定理に基づくと、適合率は感度と特異度から計算できることが分かります。ここで、検査陽性の適合率をPC(T)、検査陰性の適合率をPC(F)としましょう。
\begin{eqnarray}
PC(T) &=& P(罹患=T|検査=T) \\
&=&
\frac{P(検査=T|罹患=T) P(罹患=T)}{P(検査=T)} \\
&=&
\frac{P(検査=T|罹患=T) P(罹患=T)}
{ P(検査=T|罹患=T) P(罹患=T) + P(検査=T|罹患=F) P(罹患=F)} \\
&=&
\frac{RC \times P(罹患=T)}
{ RC \times P(罹患=T) + (1 - SP) \times P(罹患=F)} \\
\\
PC(F) &=& P(罹患=F|検査=F)\\
&=&
\frac{P(検査=F|罹患=F) P(罹患=F)}{P(検査=F)} \\
&=&
\frac{P(検査=F|罹患=F) P(罹患=F)}
{ P(検査=F|罹患=T) P(罹患=T) + P(検査=F|罹患=F) P(罹患=F)} \\
&=&
\frac{SP \times P(罹患=T)}
{ (1-RC) \times P(罹患=T) + SP \times P(罹患=F)} \\
\end{eqnarray}
また、正解率も同様にして、
\begin{eqnarray}
AC &=& P(検査=T,罹患=T) + P(検査=F,罹患=F) \\
&=&
P(検査=T|罹患=T)P(罹患=T) + P(検査=F|罹患=F)P(罹患=F) \\
&=&
RC \times P(罹患=T) + SP \times P(罹患=F)
\end{eqnarray}
と書けます。
Pythonで計算してみる
では、Pythonを使って、検査陽性の適合率PC(T)、検査陰性の適合率PC(F)、正解率(AC)を計算してみましょう。
前提条件
前提条件として、以下の仮定を使います。
- 再現率(=感度)RCは0.7
- 特異度SPは0.95
- 事前確率P(罹患=T)およびP(罹患=F)をパラメータとする。
上で述べたようにこれらの真値は分からないので、色々と変更してシミュレーションしてみるのもいいかもしれません。
ライブラリをインポートします。
import numpy as np
import matplotlib.pyplot as plt
検査陽性の適合率PC(T)、検査陰性の適合率PC(F)、正解率(AC)を計算する関数を定義します。引数として、事前確率P(罹患=T)とパラメータを与えます。
def PCT(p, key):
rc = key['rc']
fp = 1. - key['sp']
return rc * p / ( rc * p + fp * (1. - p))
def PCF(p, key):
sp = key['sp']
fn = 1. - key['rc']
return sp * (1. - p) / ( fn * p + sp * (1. - p))
def AC(p, key):
rc = key['rc']
sp = key['sp']
return rc*p + sp*(1. - p)
事前確率P(罹患=T)を変えて計算する部分です。0に近い部分でメッシュを細かくするようにしています。
key = {'rc' : 0.7, 'sp' : 0.95 }
pp = [ np.exp( - 0.1 * i) for i in range(0,100)]
pct = [ PCT( p, key) for p in pp]
pcf = [ PCF( p, key) for p in pp]
ac = [ AC( p, key) for p in pp]
グラフを表示する部分です。
plt.rcParams["font.size"] = 12
fig, ax = plt.subplots(figsize=(10,5))
ax.plot(pp, pct)
ax.plot(pp, pcf)
ax.plot(pp, ac)
ax.legend(['precision (infected)','precision (non-infected)','accuracy'])
xw = 0.1; xn = int(1./xw)+1
ax.set_xticks(np.linspace(0,xw*(xn-1), xn))
yw = 0.1; yn = int(1./yw)+1
ax.set_yticks(np.linspace(0,yw*(yn-1), yn))
ax.grid(which='both')
ax.set_xlabel('positive ratio (prior probability)')
plt.show()
シミュレーション結果
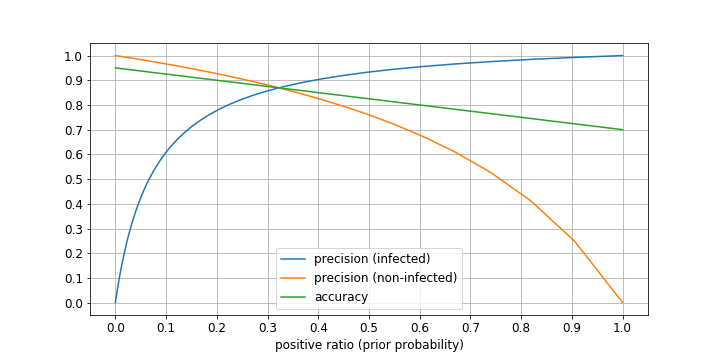
このグラフから以下の傾向が読み取れます。
- 検査陽性の適合率PC(T)に関しては、事前確率P(罹患=T)が低いとかなり悪化し、P(罹患=T)=0.1のとき、検査陽性でも罹患している確率は60%程度である。
- 検査陽性の適合率PC(F)に関しては、事前確率P(罹患=T)が高いとかなり悪化し、P(罹患=T)=0.9のとき、検査陰性でも罹患していない確率は25%程度である。
- 正解率(AC)は、特異度と感度を線形補完する形状であり、両方とも値が高いに越したことはない。
さらに、もう一歩考察
検査を実施する意義を考えると、検査陽性の適合率も、検査陰性の適合率も隔離を判断する上で重要ですが、それ以外にも、以下の指標が重要であると考えられます。
- 嘘陽性率:検査陽性でも罹患していない確率、P(罹患=F|検査=T):何故なら、検査陽性なら隔離しなければならない法律になっているので、その分無駄に病院のベッドを埋めてしまうからです。
- 嘘陰性率:検査陰性でも罹患している確率、P(罹患=T|検査=F):何故なら、検査陰性だと安心してマスクなどの対策をせずに周囲に感染を広めてしまう可能性があるからです。
※偽陽性率はP(検査=T|罹患=F)、偽陰性率はP(検査=F|罹患=T)と定義されるため、敢えて、P(罹患=F|検査=T)を嘘陽性率、P(罹患=T|検査=F)を嘘陰性率という言葉にしました。造語です。
上記の指標は以下で計算できます。
\begin{eqnarray}
嘘陽性率:FP &=& P(罹患=F|検査=T) = 1 - P(罹患=T|検査=T) = 1 - PC(T) \\
嘘陰性率:FN &=& P(罹患=T|検査=F) = 1 - P(罹患=F|検査=F) = 1 - PC(F) \\
\end{eqnarray}
これらの値を計算して表示してみましょう。
fp = [1. - p for p in pct]
fn = [1. - p for p in pcf]
plt.rcParams["font.size"] = 12
fig, ax = plt.subplots(figsize=(10,5))
ax.plot(pp, fp)
ax.plot(pp, fn)
ax.legend([ 'fake positive', 'fake negative' ])
xw = 0.1; xn = int(1./xw)+1
ax.set_xticks(np.linspace(0,xw*(xn-1), xn))
yw = 0.1; yn = int(1./yw)+1
ax.set_yticks(np.linspace(0,yw*(yn-1), yn))
ax.grid(which='both')
ax.set_xlabel('positive ratio (prior probability)')
plt.show()
当たり前ですが、嘘陽性率は検査陽性の適合率PC(T)と、嘘陰性率は検査陰性の適合率PC(F)と逆の関係になっています。
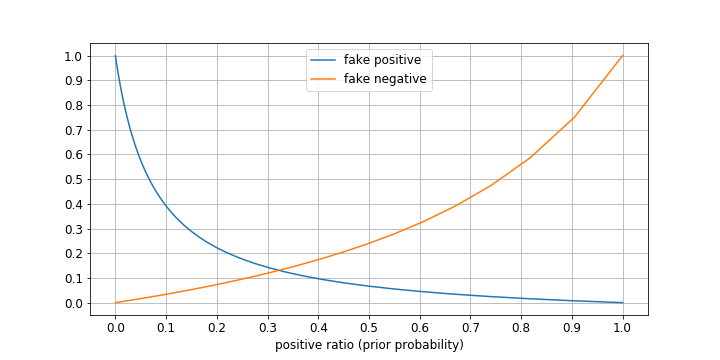
このグラフから以下の傾向が読み取れます。
- 嘘陽性率に関しては、事前確率P(罹患=T)が低いとかなり悪化し、P(罹患=T)=0.1のとき、検査陽性でも罹患していない確率は40%程度である。
- 嘘陰性率に関しては、事前確率P(罹患=T)が高いとかなり悪化し、P(罹患=T)=0.9のとき、検査陰性でも罹患している確率は75%程度である。
考察
以上から、COVID-19感染症へのPCR検査に関して、次の傾向がシミュレーションから導けます。なお、数値に関しては、感度・特異度の真値があくまで推定値であることに注意が必要です。
- 事前確率P(罹患=T)が低いと、検査陽性の適合率も嘘陽性率も悪化し、概ね$P(罹患=T) \leq 0.1$では害が多く、$P(罹患=T) \geq 0.2$なら陽性の適合率が8割程度期待できる。
- 事前確率P(罹患=T)が高いと、検査陰性の適合率も嘘陰性率も悪化し、概ね$P(罹患=T) \geq 0.9$では害が多く、$P(罹患=T) \leq 0.45$なら陰性の適合率が8割程度期待できる。
さらに言えば・・・
- 厚生労働省が、濃厚接触者や、発熱などの症状があり、インフルエンザ等の検査が陰性で、医者が必要と認めた場合のみPCR検査を推奨しているのは、事前確率P(罹患=T)を高めているという意味で極めて合理的です。
- 希望する100万人に対して、事前のスクリーニングもなく誰でもPCR検査を受けられるようにするということは、事前確率を極めて低くする行為であり、仮に本当に罹患している人数が1万人以下、$P(罹患=T) \leq 0.01$とすると、嘘陽性率は87.5%以上となり、医療のリソースを過剰に無駄に浪費するものと思われます。
- 韓国、ドイツだけでなく、アメリカもドライブスルー検査を導入しようとしているようですが、とても心配ですね。
参考リンク
下記のページを参考にさせて頂きました。
[病原体検出マニュアル2019-nCoV Ver.2.8]
(https://www.niid.go.jp/niid/images/lab-manual/2019-nCoV20200304v2.pdf)
[PCR実験の手引き]
(http://www.takara-bio.co.jp/kensa/pdfs/book_1.pdf)
F値
ベイズの定理