Juliaでバーチャル地球儀を作ってみた

はじめに

　Python並みに書きやすく、C++並みに速いという噂のJuliaに興味を持ち、試しに重た目のプログラムを書いてみました。
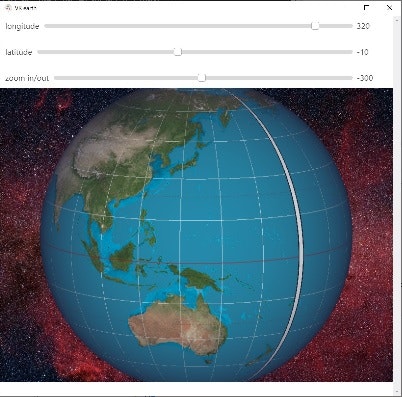
　やりたいことは、地球をグリグリ回して表示する地図アプリです。

インストールしたもの

• [Julia 1.4.2] (https://julialang.org/)
• anaconda3にJulia用の環境を追加
• Jupyter Notebookを追加
• Julia用の各種パッケージ(Blink, ImageMagick, ImageView, Images, Interact, Plots, WebIO, IJulia(※Jupyter用))

普段Pythonを使っているので、anacondaで環境を分けました。
JuliaからPythonのmatplotlibなどを使うためにPython連携があると便利なようです。

作ったアプリ

見た目はこんな感じです。スライダーでグリグリ地球を回します。ズームもできます。
(2020/6/28追記)とりあえず、どんなアプリか試してみたい人向けに、Windows10用のバイナリ(exe)を用意しました。（JuliaではなくPython版です）
GitHub:VRMapEarthApp.exe

コンセプト

開発コンセプトはこんな感じです。

• 正距円筒図法(Equirectangular projection)で描かれた地図を3Dの真球にマッピングする。
• 地軸の角度と地軸を中心とした回転でグリグリ回す。
• １点透視図法により、ズームイン・ズームアウトに対応。
• 簡易レイトレーシング。陰影も付ける。
• 背景も付ける。
• Juliaの関数型言語っぽい特徴を使って、関数の合成をしまくる。

幾何学的な部分

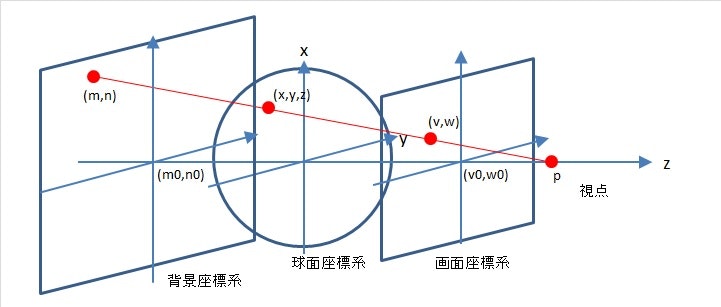
下図のような関係にある、視点、画面座標系、球面座標系、背景座標系の
視点からの直線（視線）との交点を計算しながら画面座標系にマッピングしていきます。

特に、重要な計算式は、視線と球面の交点(x,y,z)から地図上の緯度・経度を求める部分です。
以下の記号を使います。

• $polerv$ : 角度$\phi$で回転された地軸
• $polerh$ : polervに直交するベクトル
• $q=(x,y,z)$ : 球面と視線の交点
• $r$ : 球面の半径
• $lat$ : 経度
• $long$ : 緯度
• $\phi$ : 地軸の回転
• $\theta$ : 地軸"周り"の回転

計算順序は以下のとおりです。

(1) polerv, polerhを設定

polerv = [0, cos(\phi), sin(\phi)] \\
polerh = [0, sin(\phi), -cos(\phi)] \\

(2) 緯度(lat)を求める

c1  = 1/r * q \cdot polerv \\
lat = arccos(c1) \\

(3) ベクトル$q$の地軸polervとの直交成分の単位ベクトルを求める。

b0 = 1/r * q - c1 * polrev \\
b = b0/||b0||

(4) 経度(long)を求める。

cv = b \times polerh \\
c2 = cv \cdot polerv \\
c3 = b \cdot polerh \\
long = arccos(c3) sign(c2) + \theta

$cv$は$b$と$polerh$との外積です。$arccos$では$[0,\pi]$しか求められないので、外積の符号で補完しています。

ソースコード

GitHubにアップロードしてあります。

okimebarun/VRMapEarth.jl

特にこだわりの部分を解説します。

計算パラメータ用の構造体です。
Dictと付いていますが、辞書だと遅そうなので構造体に変えています。

mutable struct ParamDict
    p::Float32  # z-axis of eye point
    r::Float32  # sphere radius
    v0::Int     # mid-point of v
    w0::Int     # mid-point of w
    m0::Int     # mid-point of m
    n0::Int     # mid-point of n
    z1::Float32 # z-axis of img-plane
    z2::Float32 # z-axis of background-plane (dont use now)
    msh::Int    # map size for longtitude
    msv::Int    # map size for latitude
end;

視線と球面との交点を求める関数です。パラメータ表示された直線$[at,bt,-t+p]$と球面の式$x^2+y^2+z^2=r^2$から導けます。

function spxyz(d::ParamDict, a::Float32, b::Float32)
    ab1 = a^2+b^2+1
    r1 = d.p^2 -(d.p^2 - d.r^2)*ab1
    if r1 < 1e-10
        (false, 0.0, 0.0, 0.0)
    else
        t = (d.p - sqrt(r1)) / ab1
        x = a*t
        y = b*t
        z = -t + d.p
        (true, x, y, z)
    end
end

視線と球面との交点の(x,y,z)から緯度経度(lat,long)および、球中心から交点へのベクトルと視線ベクトルのなす角度のcosを、反射係数用に求めています。

function polerax(d::ParamDict, x::Float32, y::Float32, z::Float32,
        long0::Int, lat0::Int)
    
    phi = pi*(Float32(lat0)/180.0+1.0)
    ax = 0
    ay = cos(phi)
    az = sin(phi)
    polerv = [ax, ay,  az] # earth's axis
    polerh = [ 0, az, -ay] # orthogonal to polerv
    
    # get latitude
    r = d.r
    c1 = [x,y,z]'*polerv/r
    lat = acos(c1*0.9999)

    # get longtitude
    # inline function
    cross3d(a,b)=[a[2]b[3]-a[3]b[2], a[3]b[1]-a[1]b[3], a[1]b[2]-a[2]b[1]]
    b  = [x,y,z]/r - polerv*c1 # projection on polerv
    b  = b/sqrt(b'*b) # unitilize
    cv = cross3d(b, polerh) # outer product
    c2 = cv'*polerv
    c3 = b' *polerh
    long = acos(c3*0.9999) * sign(c2)+ pi*Float32(long0)/180.0   
    
    # convert to 360 / 180 degree
    long2 = Float32(360.0*(long/(2pi) + 2.0) % 360.0) # Mod on float
    lat2  = Float32(180.0*( lat/(pi)  + 2.0) % 180.0)

    # reflection coefficient
    coef = [x, y, z]'*[0.0, 0.0, 1.0]/d.r
    (long2, lat2, coef)
end

画面座標から、以下の結果を計算する関数です。

• 球面と視線が交わる場合、地図上の位置と反射係数
• 球面と視線が交わらない場合、背景上の位置

関数を繋げて素直に計算できるのがいいですね。

function convToMap(d::ParamDict, w::Int, v::Int, long0::Int, lat0::Int)
    (a,b) = imcoef(d, v, w)
    (bon, x, y, z) = spxyz(d, a, b)
    if bon
        (long, lat, coef) = polerax(d, x,y,z, long0, lat0)
        (mx, my) = mapxy(d, long, lat)
        (true, my, mx, coef)
    else
        (m, n) = backax(d, v, w)
        (false, n,  m, 0.0)
    end
end

画面座標系のピクセルpから地球画像もしくは背景画像の対応ピクセルを返す関数です。
RGB{N0f8}型を使うと大変簡単に書けます。

    # convert to image
    function imconv1(p)
        # shade effect
        rgb0 = RGB{N0f8}(0.1,0.1,0.2)
        # select pixel from two images depending on the first flag
        p[1] ? RGB{N0f8}( img_earth[p[2],p[3]]*p[4] + rgb0*(1.0-p[4]) ) : img_galaxy[p[2],p[3]]
    end

スライダーの情報と画面座標系からカラーイメージを返す関数です。
ドット(.)を使うと、２次元配列計算がfor文なしで書ける！のがいいですね。

    # visualize the result
    function view1(long::Int, lat::Int, z1::Float32, d1=d1, ws=ws, vs=vs)
        d1.z1 = z1
        imap1a(w,v)=convToMap(d1, w, v, long, lat)
        # Julia like mapping!
        m   = imap1a.( ws, vs' )
        img = imconv1.(m)
        colorview(RGB, img)
    end

Juliaを使ってみた感想

個人的にJuliaを初めて使ってみた感想です。

良かった点

• 数学の記述っぽく素直にプログラミングできる。
• 関数がメタっているので再利用しやすい。C++のtemplateみたいな感じか。
• atan(Inf)などが普通に計算できる！ゼロ割気にしないでいい。
• ドット（例：func.(x)）が凄く使いやすい。
• ライブラリがそれなりに充実している。

悪かった点

• using SomePackageするたびにコンパイルが始まる…。遅いです。キャッシュして(-_-;)。
• Interact.jlはJupyter NotebookではOKだったのに、Jupyter Labで使えなかった。（そのうち改善？）
• 関数によっては型が対応してないので、いちいちキャストが必要。
• 謎の丸め誤差が生じる場合がある。Float64使えば良かったのかな？

興味が湧いた点

• 高速化。分散計算やGPUなど、色々。
• シミュレーション。数式が書きやすいので色々試しやすそう。
• UIアプリ化。Interact.jlはシンプルで使いやすい。

参考リンク

下記のページを参考にさせて頂きました。

Juliaの画像処理ライブラリを使ってわかったこと
Interact.jl を用いて Julia で使う対話機能を持つ可視化ソフトを作ろう
実例で学ぶJuliaプログラミング言語入門
1から始める Juliaプログラミング
Equirectangular projection
高品質なフリー画像素材