概要
MDR社が開発した、イジングモデルを扱った開発ツールWildqat(http://mdrft.com/wildqat/) のチュートリアルを行いました。
本記事ではそこで出た疑問やちょっとしたメモなどを書いておきます。(全然ちょっとしたメモじゃない)
チュートリアルは以下から飛べます。
https://github.com/mdrft/Wildqat/tree/master/examples_ja
チュートリアル1からチュートリアル4までは前の記事(https://qiita.com/okd46/items/92f2855b37f79112e7c5) を参照。
チュートリアル5
グラフ$G=(V, E)$が与えられたとき
…?
ということで、本チュートリアルで使うグラフ理論の知識をピックアップします。
グラフ理論について
点集合$V$、辺集合$E$からなるグラフ$G(V, E)$について考えます。(ということで良いのですかね?)
今回のチュートリアルで考えるグラフは以下のものです。
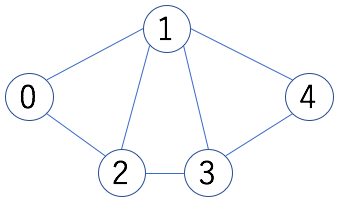
書き方が正しいのかわかりませんが、
\begin{align}
V &= \{ 0, 1, 2, 3, 4\}\\
E &= \{\overline{01}, \overline{02},\overline{12}, \overline{13}, \overline{14}, \overline{23},\overline{34}\}
\end{align}
ということですね。
部分グラフ
二つのグラフ ${\displaystyle G}$ と ${\displaystyle G'}$ について、 $G'$ の頂点集合と辺集合が共に $G$ の頂点集合と辺集合の部分集合になっているとき、 $G'$は $G$ の部分グラフ[英 18]である、または $G$ は $G'$の拡大グラフであるといい、$G'\subseteq G$ と表す[8]。
(Wikipediaより引用)
今回の例で見ると
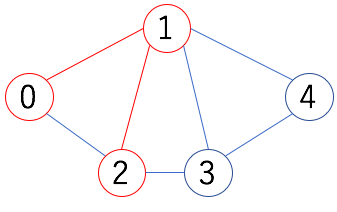
赤の部分が部分グラフですね。
$\overline{02}$は塗り忘れではなく、部分グラフでは必ずしも抜き出した頂点同士で結ばれている線を全て結ぶ必要はありません。
全て結んである部分グラフは誘導グラフという別の名前がついています。
誘導部分グラフ
また、 $G$ の頂点集合 $V$ の部分集合 $U$ を取り出して、両端点が $U$ に属する全ての辺を辺集合とする G の部分グラフ $G[U]$ を、誘導部分グラフ[英 20]という。
(Wikipediaより引用)
上でも説明しましたが、これですね。
これは以下で説明するクリークでもあります。
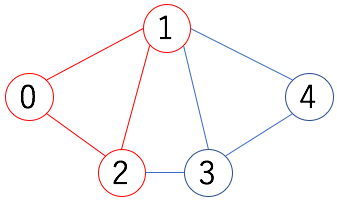
完全グラフ
完全グラフ(英: complete graph)は、任意の 2 頂点間に枝があるグラフのことを指す。
(Wikipedia より引用)
Wikipediaのリンクにある例を見れば一目瞭然かと思います。
クリーク
また、完全グラフになる誘導部分グラフのことをクリークという[1]。
(Wikipedia より引用)
下の図の赤で塗られた誘導部分グラフは $K_2$:2 頂点の完全グラフになっていますね。同じく緑の誘導部分グラフは $K_3$ になっていますね。
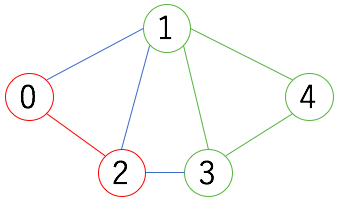
解きたい問題
今回は上の図のような、それぞれの部分グラフがクリークになるような分割の仕方を求めたいわけです。
(解の一つが上の図、ということですね。)
コスト関数
頂点$v$を色$i$で塗り分けるかどうかを$x_{v,\ i}$と表すことにします。
これは頂点 0 が色 0 で塗られていれば(色1では塗られていない) $x_{0,\ 0} = 1, \ x_{0,\ 1} = 0$ ということですね。
これを使うとコスト関数は
H = A \sum_v \left(1-\sum_{i=1}^{n}x_{v,\ i}\right)^2 + B \sum_{i=1}^n\left[\frac{1}{2}\left(-1+\sum_v x_{v, \ i}\right)\sum_v x_{v, \ i}-\sum_{(uv) \in E} x_{u, \ i}x_{v, \ i}\right]
となるらしいですが、さっぱりですね。
チュートリアルと同様に一項目から見ていきましょう。
\sum_v \left(1-\sum_{i=1}^{n}x_{v,\ i}\right)^2
について
各頂点$v$について、ただ一つの色で塗られているとき最小値0をとります。
とあります。
これはすぐわかると思います。
普通に考えると頂点は一色で塗るもんでしょ、と思いますが、0, 1で表現するので、例えば全部1(=全ての色で塗られている)という結果にもなりかねません。
ですので、コスト関数をこのように置くことで、ただ一つの色で塗ってもらいます。
次に二項目ですね。
\sum_{i=1}^n\left[\frac{1}{2}\left(-1+\sum_v x_{v, \ i}\right)\sum_v x_{v, \ i}-\sum_{(uv) \in E} x_{u, \ i}x_{v, \ i}\right]
$\sum_{i=1}^n\frac{1}{2}\left(-1+\sum_v x_{v, \ i}\right)\sum_v x_{v, \ i}$の部分は色$i$で塗られている頂点の数$\sum_v x_{v, \ i}$を$n_i$とおくと ${}_nC_2$と一致します。これは色$i$で塗られた頂点からなる完全グラフの辺の数と一致します。
とあります。確かに、 $\sum_v x_{v, \ i}$ を $n_i$ とおくと
\begin{align}
\frac{1}{2}\left(-1+\sum_v x_{v, \ i}\right)\sum_v x_{v, \ i} &= \frac{(n_i-1)n_i}{2}= {}_{n_i}C_2
\end{align}
となります。
頂点の数が $n_i$ 個ならば、 $\dbinom{n_i}{2}$ が全ての頂点から二つの頂点を選ぶことに一致する、ということはわかる、というか当然ですよね。
また、完全グラフは任意の 2 頂点間に辺があるので、辺の数が $\dbinom{n_i}{2}$ と一致しますね。
続いて後半です。
\sum_{(uv) \in E} x_{u, \ i}x_{v, \ i}
まず $(uv) \in E $ は考えているグラフにおける全ての辺について和を取る、ということですね。

この例で考えると、
\begin{align}
\sum_{(uv) \in E} x_{u, \ i}x_{v, \ i} &= x_{0, \ i}x_{1, \ i} + x_{0, \ i}x_{2, \ i} + x_{1, \ i}x_{2, \ i} + x_{1, \ i}x_{3, \ i} + x_{1, \ i}x_{4, \ i} + x_{2, \ i}x_{3, \ i} + x_{3, \ i}x_{4, \ i}
\end{align}
ですね。
$i = 0$ (=赤)なら、
\begin{align}
\sum_{(uv) \in E} x_{u, \ 0}x_{v, \ 0} &= 1\ \ \ \ (x_{0, \ 0}x_{2, \ 0}\textrm{のみ})
\end{align}
$i = 1$ (=緑)なら、
\begin{align}
\sum_{(uv) \in E} x_{u, \ 1}x_{v, \ 1} &= 3\ \ \ \ (x_{1, \ 1}x_{3, \ 1},\ x_{1, \ 1}x_{4, \ 1},\ x_{3, \ 1}x_{4, \ 1})
\end{align}
ですね。これらの値は、完全グラフの辺の数と一致していることがわかります。
逆に
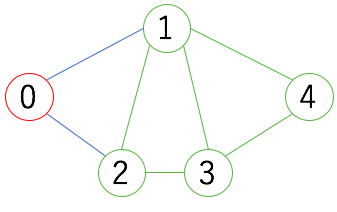
このグラフにおいて緑を考えると
\begin{align}
\sum_{(uv) \in E} x_{u, \ 1}x_{v, \ 1} &= 5\ \ \ \ (x_{1, \ 1}x_{2, \ 1},\ x_{1, \ 1}x_{3, \ 1},\ x_{1, \ 1}x_{4, \ 1},\ x_{2, \ 1}x_{3, \ 1},\ x_{3, \ 1}x_{4, \ 1})
\end{align}
となり、($\ne {}_4C_2$なので)完全グラフでないことを示しています。
これらの例から
後半の$\displaystyle \sum_{(uv) \in E} x_{u,i}x_{v,i}$の部分は色$i$で塗られている部分グラフに含まれる実際の辺の数を表しています。これはその部分グラフが完全グラフだった場合に限り、前者の値($ {}_{n_i} C _2$)と同じになるので、(以下略)
この文が理解できます。
この後の式変形は(多分)問題なく出来ると思います。
問題を解く流れ
とりあえずコード全体を見てみてもわからないので、ひとつずつ見ていきましょう。
隣接行列
まずはグラフを行列に落とし込みます。
グラフ理論には隣接行列(adjacency matrix)という概念があるようなので、こちらを用いるようです。隣接行列-wikipedia
adjacency_matrix = \
[ \
[0,1,1,0,0], \
[1,0,1,1,1], \
[1,1,0,1,0], \
[0,1,1,0,1], \
[0,1,0,1,0], \
]
これは頂点 $i$ と頂点 $j$ が枝で繋がっていたら $(ij)$成分が 1 、繋がっていなかったら 0 となります。
具体的に見ていきましょう。
最初の[0,1,1,0,0]ですが、 0 から繋がっている枝は 1 と 2 ですので、 1(二番目)と 2 (三番目)が 1 になりほかは 0 になります。
他も同様です。
QUBO作成
チュートリアルでのコードは以下のとおりです。
def get_qubo(adjacency_matrix, n_color, A, B):
graph_size = len(adjacency_matrix)
qubo_size = graph_size * n_color
qubo = np.zeros((qubo_size, qubo_size))
indices = [(u,v,i,j) for u in range(graph_size) for v in range(graph_size) for i in range(n_color) for j in range(n_color)]
for u,v,i,j in indices:
ui = u * n_color + i
vj = v * n_color + j
if ui > vj:
continue
if ui == vj:
qubo[ui][vj] -= A
if u == v and i != j:
qubo[ui][vj] += A * 2
if u != v and i == j:
qubo[ui][vj] += B * 0.5
if adjacency_matrix[u][v] > 0:
qubo[ui][vj] -= B
return qubo
n_color = 2
A = 0.1
B = 0.1
annealer = wq.opt()
annealer.qubo = get_qubo(adjacency_matrix, n_color, A, B)
関数、get_quboで指定する引数は、隣接行列、塗る色の数、コスト関数の係数A、Bですね。
チュートリアルでは隣接行列は先述のもの、塗る色の数は 2 、 係数はともに 0.1 ですね。
丁寧すぎるかも知れませんが、一行ずつ見ていきましょう。
graph_size = len(adjacency_matrix)
本チュートリアルでは graph_size = 5 となり、これは頂点の数と一致します。
qubo_size = graph_size * n_color
qubo_size は 5 × 2 で 10 となりますね。これは各頂点がどの色で塗られているのか表現するのに十分な数ですね。
qubo = np.zeros((qubo_size, qubo_size))
もちろん qubo は 10 × 10 の行列になりますね。
indices = [(u,v,i,j) for u in range(graph_size) for v in range(graph_size) for i in range(n_color) for j in range(n_color)]
ここでは (0, 0, 0, 0) から (4, 4, 1, 1) までの tuple が格納されているリストを作成します。
これらをどう使うか見ていきましょう。
for u,v,i,j in indices:
ui = u * n_color + i
vj = v * n_color + j
if ui > vj:
continue
if ui == vj:
qubo[ui][vj] -= A
if u == v and i != j:
qubo[ui][vj] += A * 2
if u != v and i == j:
qubo[ui][vj] += B * 0.5
if adjacency_matrix[u][v] > 0:
qubo[ui][vj] -= B
ui, vj がQUBOのインデックスとなっており、 0 -> 頂点0色0、 1 -> 頂点0色1、 2 -> 頂点1色0、…となっていますね。
ui > vj で continue となっているのはQUBOの左下を 0 にするためですね。
先にコスト関数から確認してみましょう。
\begin{align}
H_{一項目} = -A\sum_v \sum_{i=1}^n x^2_{v, i}
\end{align}
$x^2_{v,i} = x_{v,i}x_{u,j} \ \ ( v\ = \ u,\ i\ = \ j)$ と捉えれば
if ui == vj:
qubo[ui][vj] -= A
となりますね。
\begin{align}
H_{二項目} = A\sum_v 2\sum\sum_{\hspace{-0.8cm}i \ne j}^{\hspace{-0.8cm}n} x^2_{v, i}
\end{align}
まず $ i \ \ne \ j $ であることがわかります その時に、$2Ax_{v, i}x_{v, j}$、を計算するので $ \ v\ =\ u$ であることもわかります。
つまり $ i\ \ne \ j || \ v\ =\ u $ であるQUBO行列成分に $2A$ を足せば良いので
if u == v and i != j:
qubo[ui][vj] += A * 2
となるのですね。
\begin{align}
H_{三項目} = \frac{1}{2}B \sum_{i=1}^n \sum\sum_{\hspace{-0.8cm}u\ne v}^{\hspace{-0.8cm}n} x_{u, i}x_{v,i}
\end{align}
これは二項目とかなり似ていますね。
$ i\ = \ j \ || \ v\ \ne\ u $ であるQUBO行列成分に $\frac{1}{2}B$ を足せば良いので
if u != v and i == j:
qubo[ui][vj] += B * 0.5
となりますね。
\begin{align}
H_{四項目} = -B \sum_{i=1}^n\sum_{(u,v) \in E}x_{u, i}x_{v, i}
\end{align}
この項は実際に考えているグラフに依存するので注意が必要ですね。
$(u, v \in E)$を考えるで、 adjacency_matrixの値が1であるもののみを考えることになります。
また、$x_{u, i}x_{v, i}$ を考えるので $ i\ =\ j $ であることもわかります。
これを踏まえると
if i == j and adjacency_matrix[u][v] == 1 :
qubo[ui][vi] -= B
となりますね。
チュートリアリアルでは $ u \ \ne \ v $ の条件も入っています(ある頂点から伸びた枝が同じ頂点に戻ることは考えていない?)が大きな影響は無いでしょう。
実際に解く
q = annealer.sa()
で解をだしていますね。
その後
calculate_H(q, adjacency_matrix, n_color, A, B)
という関数を通しているので、関数を見てみます。
def calculate_H(q, adjacency_matrix, n_color, A, B):
graph_size = len(adjacency_matrix)
h_a = calculate_H_A(q, graph_size, n_color, A)
h_b = calculate_H_B(q, adjacency_matrix, n_color, B)
print(f"H = {h_a + h_b}")
return h_a + h_b
def calculate_H_A(q, graph_size, n_color, A):
hamiltonian = 0
for v in range(graph_size):
sum_x = 0
for i in range(n_color):
index = v * n_color + i
sum_x += q[index]
hamiltonian += (1 - sum_x) ** 2
hamiltonian *= A
print(f"H_A = {hamiltonian}")
return hamiltonian
def calculate_H_B(q, adjacency_matrix, n_color, B):
graph_size = len(adjacency_matrix)
hamiltonian = 0
for i in range(n_color):
sum_x = 0
for v in range(graph_size):
vi = v * n_color + i
sum_x += q[vi]
for u in range(graph_size):
if u >= v:
continue
ui = u * n_color + i
hamiltonian -= adjacency_matrix[u][v] * q[ui] * q[vi]
hamiltonian += 0.5 * (-1 + sum_x) * sum_x
hamiltonian *= B
print(f"H_B = {hamiltonian}")
return hamiltonian
細かく見ていきます。
graph_size = len(adjacency_matrix)
h_a = calculate_H_A(q, graph_size, n_color, A)
h_b = calculate_H_B(q, adjacency_matrix, n_color, B)
最初にgraph_sizeを計算した後、A と B で分かれていますね。
A から見ていきましょう。
hamiltonian = 0
for v in range(graph_size):
sum_x = 0
for i in range(n_color):
index = v * n_color + i
sum_x += q[index]
hamiltonian += (1 - sum_x) ** 2
hamiltonian *= A
print(f"H_A = {hamiltonian}")
return hamiltonian
次にhamiltonianという変数を用意して0で初期化。
その後、sum_xに各頂点について、その頂点が何色の色で塗られているかを入れていますね。
もちろん、1 になるのがベストです。
その後、hamiltonian に (1 - sum_x) ** 2 を足しています。
これは、 各頂点が一色で塗られている時に最小になりますね。
その後、係数 A をかけて、返してます。
calculate_H_A が実際にコスト関数の値がいくらになっているか、計算している関数だということがわかります。
次に calculate_H_B を見てみましょう。
def calculate_H_B(q, adjacency_matrix, n_color, B):
graph_size = len(adjacency_matrix)
hamiltonian = 0
for i in range(n_color):
sum_x = 0
for v in range(graph_size):
vi = v * n_color + i
sum_x += q[vi]
for u in range(graph_size):
if u >= v:
continue
ui = u * n_color + i
hamiltonian -= adjacency_matrix[u][v] * q[ui] * q[vi]
hamiltonian += 0.5 * (-1 + sum_x) * sum_x
hamiltonian *= B
print(f"H_B = {hamiltonian}")
return hamiltonian
こちらも hamiltonian を 0 で初期化。
その後が逆になっているので注意が必要ですが、sum_x には、各色について、何個の頂点がその色で塗られているかを代入しています。
その後 hamiltonian を - adjacency_matrix[u][v] * q[ui] * q[vi] で引いていますね。
adjacency_matrix[u][v] は頂点 u と頂点 v がつながっているかどうか、 q[ui] * q[vi] は 頂点 u および 頂点 v が同じ色 i で塗られていれば 1 になります。
つまり、今考えているグラフで頂点 u と 頂点 v が実際に繋がっており、かつ同じ色で塗られている場合にのみ、ハミルトニアンが小さくなります。
これは、同じ色で塗られた部分グラフがクリークであればハミルトニアンの値が最小になると言い換えることも出来ますね。
その後 show_answer で実際にどの頂点がどの色で塗られたかを出力してくれます。
チュートリアル6
前提知識はチュートリアル5と同じです。
要約すると、頂点の数(サイズ)を指定して、クリークになっている頂点番号を求める、ということですね。
下の図だと、サイズを 4 と指定したら、(0, 1, 2, 3)、サイズを 3 と指定したら、(0, 1, 2)、(0, 1, 3)など、が解として欲しい、ということです。
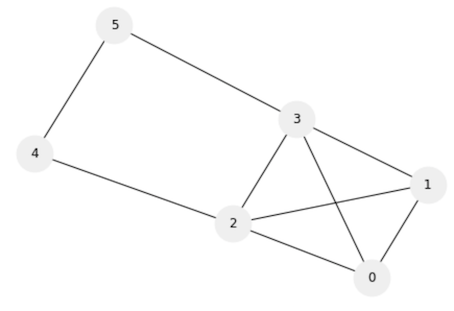
コスト関数
本文によればコスト関数は以下のようになるようです。
\begin{align}
E = \left(K-\sum_v x_v \right)^2 + B\left[ \frac{K(K-1)}{2} - \sum_{(u,\ v) \in E } x_ux_v\right]
\end{align}
まず$x_v$ですが、例えば全部で頂点が6つ(0, 1, 2, ..., 5)あり、答えが0 ,1 ,4であれば
\begin{align}
x = [1,\ 1,\ 0,\ 0,\ 1,\ 0]
\end{align}
となります。
これを踏まえてまず一項目を考えてみましょう。
一項目は、選ばれる頂点の数と、指定したクリークのサイズ($K$)が一致するときに最小になりますね。
二項目($B$がついているもの全てを指しています)の一つ目は${}_KC_2$ですね。
ここでチュートリアル5を思い出してください。
本文に
$ {}_{n_i} C _2$と一致します。つまり全ての頂点から二つの頂点を選ぶ組み合わせとなります。これは色$i$で塗られた頂点からなる完全グラフの辺の数と一致します。
と書いてありますね。
コード
チュートリアルにすごく丁寧に書かれてあるので省略します。
チュートリアル7
チュートリアル本文のExact Cover問題の説明文が抽象的だったので、具体例を出しながら補足します。
ある自然数の集合$U$を考えます。例えば$U = \lbrace 1,\ 2,\ 3,\ 4,\ 5,\ 6,\ 7,\ 8,\ 9,\ 10 \rbrace$であるとしましょう。またその自然数(もちろん1~10)を含むいくつかのグループ$V_1,\ V_2,\ , \cdots,\ V_N$を想定します。例えば$V_1 = \lbrace1,\ 2\rbrace,\ V_2 = \lbrace3,\ 4,\ 5\rbrace,\ V_3 = \lbrace 6,\ 7,\ 8,\ 9,\ 10 \rbrace, V_4 = \lbrace 1,\ 3,\ 5\rbrace,V_5 = \lbrace6,\ 7,\ 8,\ 9\rbrace ,\ V_6 = \lbrace10\rbrace$としましょう。(例でもそうなっているように)一つの自然数が複数のグループに属していても構いません。さて、そのグループ$V_i$からいくつかをピックアップした時に、それらに同じ自然数が複数含まれず、$U$に含まれる自然数セットとおなじになるようにピックアップする問題をExact Cover問題といいます。この例では、$V_1, V_2, V_3$または$V_1, V_2, V_5, V_6$が選ばれれば良い、ということですね。さらに、選んだグループ数を最小になるようにするものを、Smallest Exact Coverといいます。この例では$V_1, V_2, V_3$が選ばれれば良い、ということですね。
とりあえず普通のExact Cover問題
コスト関数とQUBO
本文中にあるように、$i$ 番目のグループをピックアップしたかどうかを$x_i \in \lbrace1,\ 0\rbrace$で表します。ピックアップされた場合は1、されなかった場合は0です。
ここで集合$U$に含まれている自然数 $\alpha$ について考えてみます。
すると
ピックアップされた1つのグループのみに含まれている場合に最小となるコスト関数$E_A$を考えます。
この場合\begin{align} E_A = A\sum_{\alpha=1}^n\left(1-\sum_{i:\alpha \in V_i} x_i\right)^2 \end{align}とすると、各自然数$\alpha$に対して1つのグループのみがピックアップされた場合、$E_A=0$となります。
ということですが、どういうことでしょうか。
まずはかっこ内の$\sum$について見てみましょう。
\begin{align}
\sum_{i:\alpha \in V_i} x_i
\end{align}
もし集合 $V_i$ が $V_1,\ V_3$ に $\alpha$ が含まれており、$V_2$ には $\alpha$ が含まれていないとしましょう。このとき
\begin{align}
\sum_{i:\alpha \in V_i} x_i = x_1 + x_3
\end{align}
となります。もしも $V_1$だけピックアップされていれば
\begin{align}
\left(1-\sum_{i:\alpha \in V_i} x_i\right)^2 = 0
\end{align}
となりますし、 $V_1,\ V_3$ の両方が選ばれていれば
\begin{align}
\left(1-\sum_{i:\alpha \in V_i} x_i\right)^2 = 1
\end{align}
となりますね。
これを $\alpha$ について和を取れば、Exact Coverになっているときに最小になる関数、つまりコスト関数になっていることがわかります。
Smallest Exact Cover問題
コスト関数とQUBO
$x_i$ が $V_i$ が選ばれているかどうかを表していることを思い出しましょう。
${V_i}$ から選ばれる集合の数が最小となれば良いので、先程のコスト関数 ($E_A$) に
\begin{align}
E_B = B \sum_i x_i
\end{align}
を加えれば良いことがわかります。
コード
こちらも丁寧に書かれてあるので省略します。
チュートリアル8
グラフ彩色問題
チュートリアルには
n色の中から1色選んで全てのノードを塗り、かつエッジで接続されているノード間は異なる色となる時の塗り方を選びます。
と書いてありますが、"各ノードそれぞれについて、n色のうち1色で塗り、かつ…"がわかりやすいと思います。(チュートリアルの表記では全てが同じ色で塗るように見えます。)
ノード = 頂点、エッジ = 辺 です。
コスト関数
これまでに見たことがあるようなコスト関数ですね。
1項目は各ノード1色に制限する制約項
これまでに見てきたとおりですね。
2項目はエッジで接続されているノード間は異なる色となる条件です。
これまでに見たもの(チュートリアル5、6)と非常に似ていますが、今回は違う色になってほしいので、係数が $-$ ではなく $+$ になっています。
チュートリアルで実際に考えるもの
6 つのノードを 4 色で塗る。
グラフは以下のようになっているとする。
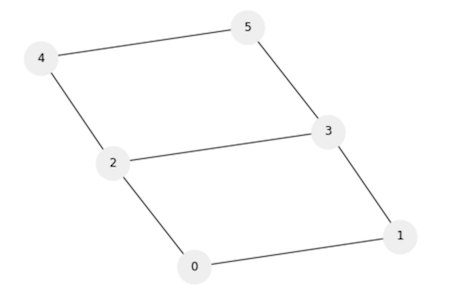
このまま考えても良いのですが、次のように言い直すことも出来ます。
1 つのノードを 4 つのノードを持つ1つのグループであるとみなし、4 つのノードのうちどの量子ビットが 1 であるかによって色を判断する。
下にこれを図示します。
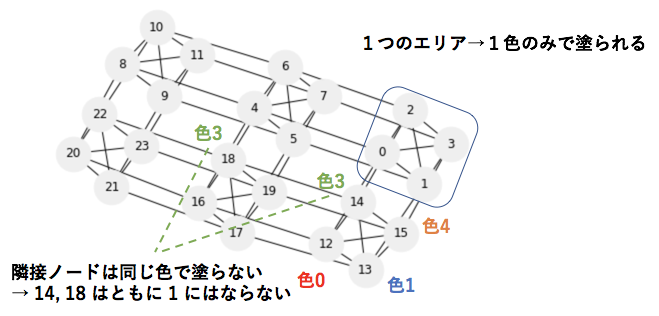
コード
まず 1 つのグループについて考えてみましょう。
1 つのグループにおける 4 量子ビットをそれぞれ $x_0,\ x_1,\ x_2,\ x_3$ とします。
ここでコスト関数が、ノードを1色に制限する制約項と、エッジで接続されているノード間は異なる色となるための項であったことを思い出します。
コスト関数の前半部分について考えてみます。
ノードを1色に制限する、ということは $x_0,\ x_1,\ x_2,\ x_3$ のいずれか 1 つのみが 1 で、他は 0 であれば良かったのでした。
つまり
\begin{align}
\left( 1- \sum_{i = 0}^3 x_i \right)^2
\end{align}
が最小になれば良いのですね。
この方法はこれまでのチュートリアルで学習済みで
one_group = [1, 1, 1, 1]
qubo_matrix += -2 * np.diag(one_group) + wq.sqr(one_group)
print(qubo_matrix)
>[[-1 2 2 2]
[ 0 -1 2 2]
[ 0 0 -1 2]
[ 0 0 0 -1]]
となるのでしたね。
これを 6 つのグループで行えば良いので
group = []
for i in range(6):
group.append(np.zeros(24))
for j in range(i*4,i*4+4):
group[i][j] = 1
matrix1 = np.zeros((24,24))
for i in range(6):
matrix1 += -2 * np.diag(group[i]) + wq.sqr(group[i])
となるのですね。
次にコスト関数の"エッジで接続されているノード間は異なる色となるための項"を考えましょう。
例えばノード 14 とノード 18 では
x_{14}x_{18} = 0
となってほしい、言い換えれば最小化してほしいので、QUBO[14][18] += B となるわけですね。
ほかの隣接するノードについても考えると
# チュートリアルとはBをかける順番を変えています
B = 1
Xarr = [[0,4],[1,5],[2,6],[3,7] , [4,8],[5,9],[6,10],[7,11] , [12,16],[13,17],[14,18],[15,19] , [16,20],[17,21],[18,22],[19,23] , [0,12],[1,13],[2,14],[3,15] , [4,16],[5,17],[6,18],[7,19] , [8,20],[9,21],[10,22],[11,23]]
matrix2 = B * wq.net(Xarr,24)
となるわけですね。
言うまでも無いですが、wildqat の net 関数は、第一引数で指定した行列要素を 1 にするものですね。
これであとは解くだけです。