本記事は、「データ構造とアルゴリズム Advent Calendar 2020」 2日目の記事です．
1日目の記事は @SaitoTsutomu 氏による「k本のハノイの塔の動かし方（Python版）」です．
3日目の記事は @At-sushi 氏による「当たり判定に役立つかもしれない４分割セグメントツリー」です．
はじめに
この記事では，「4人のロシア人の方法 (Method of Four Russians)」と呼ばれるテクニックを用いて，2つの文字列の編集距離を計算するアルゴリズムについて解説します．
対象読者
- 「編集距離を求める $ O(n^2) $ 時間の動的計画法のアルゴリズム」と聞いてピンとくる方．
編集距離を求める二乗時間アルゴリズムをご存知ない場合は，各自ぐぐってみてください．
Wikipedia やこちらのブログ記事 などが参考になると思います．
編集距離 （レーベンシュタイン距離）
ここでは，今回メインで扱う編集距離について説明します．
突然ですが，「2つの文字列がどれだけ似ているか？」ということを考えてみましょう．
例えば Qiita と Quite という2つの文字列を考えてみると，これらは何となく似ている気がします．
一方で Qiita と GitLab という2つの文字列を考えてみると，これらはあまり似ていないような気がします．
このように2つの文字列を比較したときに"どれだけ似ているか?"または"どれだけ異なっているか?"を表す指標がいくつか知られています．
編集距離は，2つの文字列のが"どれだけ異なっているか？"を表す指標のひとつです．
編集距離の具体的な定義は後述しますが，Qiita と Quite の編集距離は 2 であり，Qiita と GitLab の編集距離は 4 です．
確かに，先程の「似ている気がする/似ていない気がする」という私の直感には反していないことがわかります．
編集距離の定義
2つの文字列 $X$ と $Y$ が与えられたとき，$X$ を $Y$ に書き換えるために必要な編集操作の最小回数を $X$ と $Y$ の編集距離1と呼び，$D(X, Y)$ と表記することにします．
ここでの編集操作は，以下に示す「挿入・削除・置換」の3つのみとします:
| 操作名 | 説明 |
|---|---|
| 挿入 | 文字列中の任意の位置（両端または文字と文字の間）に1文字を挿入する． |
| 削除 | 文字列中の任意の1文字を削除する． |
| 置換 | 文字列中の任意の1文字を別の1文字に置換する． |
例えば， $X = $Qiita, $Y = $GitLab とすると，$D(X, Y) = 4$ となります．
この $4$ という値とそれに対応する編集操作列は，後述するアルゴリズムによって計算することができます．
実際に，4回の編集操作で Qiita を GitLab に書き換えられることを確認してみましょう:
| 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|
Q |
i |
i |
t |
a |
|
↓ Q を G に置換 |
| 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|
G |
i |
i |
t |
a |
|
↓ 2番目の文字 i を削除 (左詰めにします) |
| 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|
G |
i |
t |
a |
||
↓ 3番目の文字と4番目の文字の間に L を挿入 |
| 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|
G |
i |
t |
L |
a |
|
↓ 末尾に b を挿入 |
| 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|
G |
i |
t |
L |
a |
b |
確かに 4 回の編集距離操作で GitLab ができました．
以下では，２つの文字列 $X$, $Y$ が与えられたときに，編集距離 $D(X, Y)$ を求める問題を考えます．
編集距離を求める二乗時間アルゴリズム (概要)
ここでは，編集距離を求めるための有名な動的計画法のアルゴリズムについて，概要を説明します．
いま，文字列 $X$ の長さを $n$, 文字列 $Y$ の長さを $m$ とします．
次の式を満たすサイズ $(n+1)(m+1)$ の表 $T[0..n][0..m]$ を考えます:
$\qquad T[i][j] = D(X[1..i], Y[1..j])$
ここで $X[1..i]$ は，$X$ の先頭 $i$ 文字を切り取った接頭辞を表します．$Y[1..j]$も同様です．
ただし，$X[1..0]$ と $Y[1..0]$ は特別に空文字列 (長さ 0 の文字列) であると定義します．
図 1. $X = \texttt{GitLab}$, $Y = \texttt{Qiita}$ に対する表 $T$.
この表 $T$ が計算できれば，求めたかった $D(X,Y) = T[n][m]$ の値がわかります．
表 $T$ の計算には，編集距離について成り立つ以下の漸化式を利用します:
各 $k$ に対して $T[k][0] = T[0][k] = k$.
各 $i \ge 1, j \ge 1$ に対して，
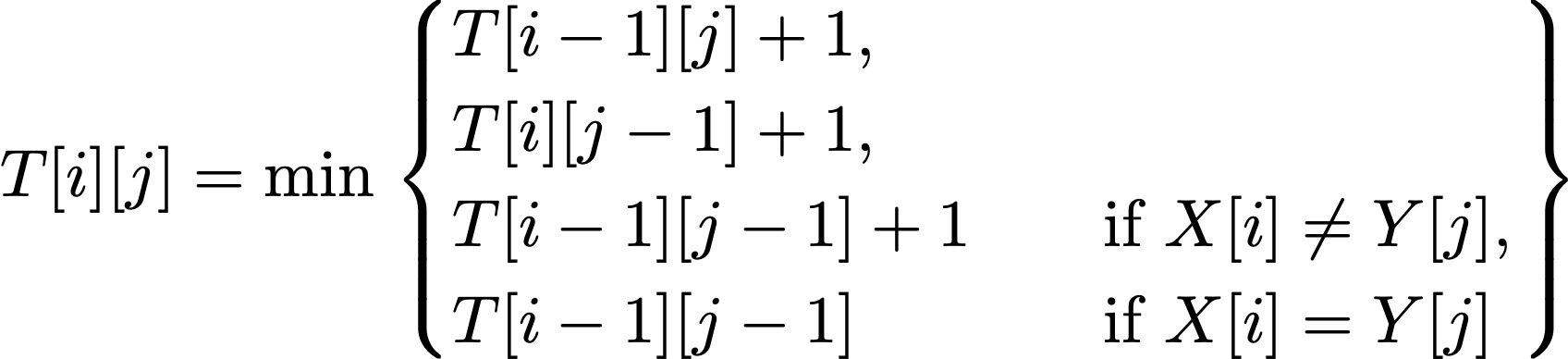
この漸化式を用いることで，表 $T$ を左上から右下に向かって，1セルあたり定数時間で埋めていくことができます．
表 $T$ のサイズは $(n+1)(m+1)$ であるので，すべてのセルを埋めても $O(nm)$ 時間におさまります2．
二乗時間より良いアルゴリズムは存在するのだろうか？
さて，編集距離を計算する $O(n^2)$ 時間のアルゴリズムが存在することがわかりました．
では，それより高速な $O(n^{1.999})$ 時間のアルゴリズムは存在するのでしょうか？
その答えは，現時点では「ないかもしれないし，あるかもしれない」です．
真面目に言うと，強指数時間仮説 (Strong Exponential Time Hypothesis; SETH) が真であるという仮定の元では，任意の非負実数 $\varepsilon > 0$ に対して，編集距離を計算する $O(n^{2-\varepsilon})$ 時間のアルゴリズムが存在しないことが知られています3．
SETH がどういった仮説であるのかは，本解説記事の範疇を超えるので割愛しますが，「その道の研究者たちが立証（または反証）しようと長年頑張っているけど真偽がわかっていない仮説だ」ということだけ把握していただければ今は十分だと思います．
もし SETH が真であると証明されれば，編集距離を計算する $O(n^{1.999})$ 時間アルゴリズムは存在しません．
逆にもし $O(n^{1.999})$ 時間アルゴリズムが見つかれば，SETH が反証されます！
というわけで，編集距離を計算する $O(n^{1.999})$ 時間アルゴリズムは存在しないか，もし存在したとしても簡単には見つからないだろう，ということで納得いただければと思います．
「4人のロシア人の方法」を用いた高速化
さて，直前の章では $O(n^{2-\varepsilon})$ 時間アルゴリズムの設計は不可能または困難そうだということがわかりました．
一方で，本記事で紹介する方法を用いることで $O(n^2 / \log_{\sigma} n)$ 時間4のアルゴリズムを設計することができます． ここで $\sigma$ は文字の種類数です．
以下では，「4人のロシア人の方法」の一般的なアイデアと，編集距離への応用について解説していきます．
「4人のロシア人の方法」の基本的なアイデアは以下の通りです:
小さい部分問題の答えを事前に計算してテーブルに格納しておき，後に大きなサイズの問題を解く際にそのテーブルを参照しながら解くことで高速化を図る．
「4人のロシア人5の方法」は，もともとは行列積計算の高速化を目的として，1970年に提案されました6．
そして1980年，Masek と Paterson は，「4人のロシア人の方法」を編集距離の計算に応用しました7．本記事で紹介する手法は Masek と Paterson の提案手法となります．
編集距離計算問題への適用
「4人のロシア人の方法」を編集距離の計算に適用します．
まずはアルゴリズム全体の概要を述べて，そのあとに前処理について具体的に考えていきます．
アルゴリズムは，前処理のフェーズと編集距離計算のフェーズの2つに分かれています．
前処理（概要）
前処理の段階では，編集距離の表 $T$ に部分構造として出現しうるサイズ $t~\times~t$ の表 (ブロックと呼ぶ) すべてに対して，その計算結果を事前に計算してテーブルに覚えておきます． ($t$ の具体的な値は，後の章で決めます．)
ここで，ブロックの左と上の境界を入力境界とよび，ブロックの右と下の境界を出力境界と呼ぶことにします．
図 2: 文字列 $\texttt{bbaab}$ と $\texttt{abbab}$ に対するブロックの概念図 ($t = 5$)．青色で塗られた部分が入力境界で，赤色で塗られた部分が出力境界．
全ブロックの答え(出力境界)が記録されたテーブルがあれば，ブロックに対応する長さ $t$ の2本の文字列およびブロックの入力境界の値が与えられたときに，そのブロックの出力境界の値を $O(t)$ 時間で計算することができるようになります．
事前計算テーブルを用いた編集距離の計算
$O(n^2)$ 時間のアルゴリズムを思い出してみると，そこではサイズ $(n+1)\times(n+1)$ の表 $T$ を用意し，その表のすべての値を左上から右下に向かって計算しました．
ここでは，表 $T$ を $t~\times~t$ のブロックに分割します．
表のサイズが $O(n^2)$ なので，ブロックの個数は $O(n^2/t^2)$ です．
図 3: 表 $T$ の分割の概念図 ($t = 5$).既存の $O(n^2)$ 時間アルゴリズムでは表 $T$ のすべてのセルを埋めていたが，今回説明する手法では緑色のセル (各ブロックの入力/出力境界) の値のみを計算することで高速化を図る．
そして，前処理で計算したテーブルを利用して，各ブロックの出力境界を $O(t)$ 時間で計算していきます．
この計算の過程では各ブロックの入力/出力境界のみを計算する (各ブロック内部の計算をスキップする) ので，合計の計算時間は $O(n^2/t^2 \times t) = O(n^2/t)$ となります．
以上が，編集距離計算問題に対する「4人のロシア人の方法」の概要です．
ここからは，前処理において作成するテーブルのサイズやその作成にかかる時間を考えます．
事前計算テーブルの作成
異なるブロックの種類数
前処理アルゴリズムの説明の中で，サイズ $t~\times~t$ のすべてのブロックに対する出力境界を計算・格納すれば十分であると述べました．
では，そのようなブロックは全部で何種類あるのでしょうか？
まず，長さ $t$ の文字列の種類数は $\sigma^t$ であるので，ブロックに対応する文字列のペアは $(\sigma^t)^2 = \sigma^{2t}$ 種類です．
次に，ブロックの入力境界の値の組合せを考えます．
表の各セルの値は長さ $n$ 以下の2本の文字列の編集距離を表すので，値の範囲は $0$ 〜 $n$ です．
入力境界の合計セル数は $2t-1$ であるので，種類数は $(n+1)^{2t-1}$ 以下であると言えます．
こうして見ると，ブロックの種類数が $n$ に対して指数的に多いように見えますが，この見積もりはかなり粗いです．
実際，編集距離と表 $T$ の定義から次の性質が成り立ちます (性質A):
隣り合うセルの値の差は $-1$, $0$, または $1$ である
性質A の正しさはここでは証明はしませんが，図 1 の例を見ると確かに性質A が成り立っていることがわかると思います．
この性質A を利用すると，ブロックの種類数は先程の見積もりよりもっと少ないことが言えます．
さらに，編集距離の値が左上から右下に向かって伝播することを考えると，ブロックの左上のセルが $0$ であるブロックに対する計算結果のみをテーブルに覚えておけば十分であることがわかります (参考: 図 4)．
図 4: 左上のセルの値が $6$ である表は，左上のセルの値を $0$ に正規化した表の各セルに $6$ を足した表と等しくなる．
性質Aより，左上のセルが $0$ であるブロックの種類数は $3^{2t-2}$ であるので，文字列のペアのすべての組合せとブロックの入力境界のすべての組合せをかけ合わせると，テーブルに覚えておくべきブロックの種類数は合計 $O((3\sigma)^{2t})$ であると言えます．
計算時間・領域
事前計算テーブルには，(ブロックに対応する2つの文字列，ブロックの入力境界) を添字として，それに対応するブロックの出力境界が要素として格納されています．
つまり，1要素あたりの使用領域は $O(t)$ ワードです8．
いま，テーブルの要素数 ( = ブロックの種類数) が $O((3\sigma)^{2t})$ であるので，事前計算テーブルが占める領域は合計で $O(t(3\sigma)^{2t})$ ワードとなります．
また，テーブルの各要素 (サイズ $t \times t$ のブロックの出力境界) は $O(t^2)$ 時間で計算できるので，前処理時間の合計は $O(t^2(3\sigma)^{2t})$ となります．
最終的な計算時間
さて，ここまでは $t$ の値は具体的に決めずに議論をしてきましたが，最後に $t$ の値を $t = (\log_{3\sigma}n)/2 \in \Theta(\log_{\sigma}n)$ とします．
すると，テーブル作成のための前処理時間が $O(t^2(3\sigma)^{2t}) = O(n(\log_{\sigma}n)^2)$,テーブルを用いて編集距離を計算する時間が $O(n^2/t) = O(n^2/\log_{\sigma}n)$ となり，合計で $o(n^2)$ 時間を達成します．
まとめ
「4人のロシア人の方法」を用いて，文字列間の編集距離を $O(n^2/\log_\sigma n)$ 時間で計算するアルゴリズムを紹介しました．
ありえるすべての小さいブロックに対する小問題の答えを事前に計算して記録しておき，のちにそれらを利用することで編集距離の計算を高速化しました．
今回は編集距離の計算という特定の問題についての解法を紹介しましたが，
小さい部分問題の答えを事前に計算してテーブルに格納しておき，後に大きなサイズの問題を解く際にそのテーブルを参照しながら解くことで高速化を図る．
というアイデア自体は，適用できる範囲がかなり広いかと思われます．
アルゴリズムの高速化を検討するときに「4人のロシア人」のことを頭の片隅に置いておくと，いいことがあるかもしれませんね．
その他の参考文献
-
M. Crochemore, G. M. Landau, M. Ziv-Ukelson. A subquadratic sequence alignment algorithm for unrestricted scoring matrices. SIAM journal on computing, 32(6), 1654–1673, 2003.
-
P. Bille, M. Farach-Colton. Fast and compact regular expression matching. Theoretical Computer Science, 409(3), 486–496, 2008.
-
B. Brubach, J. Ghurye. A Succinct Four Russians Speedup for Edit Distance Computation and One-against-many Banded Alignment. In Proc. CPM 2018, 13:1–13:12, 2018
-
N. C. Jones, P. A. Pevzner (著). 渋谷 哲朗, 坂内 英夫(訳). バイオインフォマティクスのためのアルゴリズム入門. 共立出版, 2007. (原著書名： An Introduction to Bioinformatics Algorithms. The MIT Press, 2004.)
-
「編集距離」は，それを発明したとされる人物の名をとって別名「レーベンシュタイン距離」とも呼ばれています． ↩
-
なお，対応する具体的な編集操作列は，表の最右下から順にトレースバックすることで追加 $O(n)$ 時間で求めることができます．
以下では，説明の簡単のため $X$ と $Y$ の長さはいずれも $n$ であるとします． ↩ -
A. Backurs, P. Indyk. Edit distance cannot be computed in strongly subquadratic time (unless SETH is false). In Proc. STOC 2015, 51–58, 2015. ↩
-
$n^2 / \log_{\sigma} n$ は $O(n^{2-\varepsilon})$ に属さないことに注意してください． ↩
-
原著論文がロシア語で書かれており，かつ著者が4人であったことから 「4人のロシア人の方法 (Method of Four Russians)」と呼ばれていますが，実際は著者4人のうちロシア人は1人だけだったそうです． ↩
-
V. L. Arlazarov, Y. A. Dinitz, M. A. Kronrod, I. A. Faradzhev, On economical construction of the transitive closure of an oriented graph. Dokl. Akad. Nauk SSSR, 194:3, 487–488, 1970. (in Russian) ↩
-
W. J. Masek, M. S. Paterson. A faster algorithm computing string edit distances. Journal of Computer and System Sciences, 20(1), 18–31, 1980. ↩
-
のちに $t \in O(\log_{\sigma}n)$ とするのですが，そうすると word packing ができて1要素あたり $O(1)$ ワードの領域に収まるはずです．この議論が成り立つがどうかは仮定する計算モデルに依存します． ↩