ワーシャルフロイド法
最短経路問題で使われるアルゴリズムの1つ。負の閉路がない限り、負の辺があっても使える。グラフ上の全ての頂点間の最短経路を探すので、計算量は$O(V^3)$となる。
ワーシャルフロイド法はその名前から難しそうな印象があって避けていた。しかし、最近競プロの精進中に実装する機会がチラホラあり、実装してみると思ったよりも簡単だったのでびっくりした。ワーシャルフロイド法が必要となった方は簡単な実装なので恐れず調べてみてほしい。
今回すること
ワーシャルフロイド法は実装が簡単だが、その裏でどんな振る舞いをしているのかイマイチ掴めなかった。簡単に最短経路を求められるといっても、裏の仕組みを知らずに使うのは自分としてはどうも気持ちが悪い。今回はいろいろ手を動かしてみながら、仕組みの理解を試みる。
C++によるコード
まずはワーシャルフロイド法のコードを見てみる。
void warshall_floyd(int n) {
for (int k = 0; k < n; k++){ // 経由する頂点
for (int i = 0; i < n; i++) { // 始点
for (int j = 0; j < n; j++) { // 終点
d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}
}
}
}
上記がC++によるワーシャルフロイド法の実装だ。グラフの表現は隣接行列。配列d[a][b]には頂点a,b間の辺のコストを入れておき、$a = b$の時は0を、a,b間の辺が存在しないときはINFを入れておく。アルゴリズムとしては、頂点iから頂点jへの経路と、頂点kを経由した場合の経路とを比較してよりコストの合計が小さい方を配列に入れる動的計画法を使っている。
見た目は単純な3重ループ。初めて競プロでこれを実装してACした時は簡単にできすぎて呆気にとられた。
次にこのプログラムがどんな振る舞いをしているのか確認してみよう。
実際に確かめてみよう!
まずは図を書きながら確かめる。
左が今回使うグラフで、右がそのグラフの隣接行列表現だ。早速手を動かしてみる。
$k = 0, i = 0$のとき
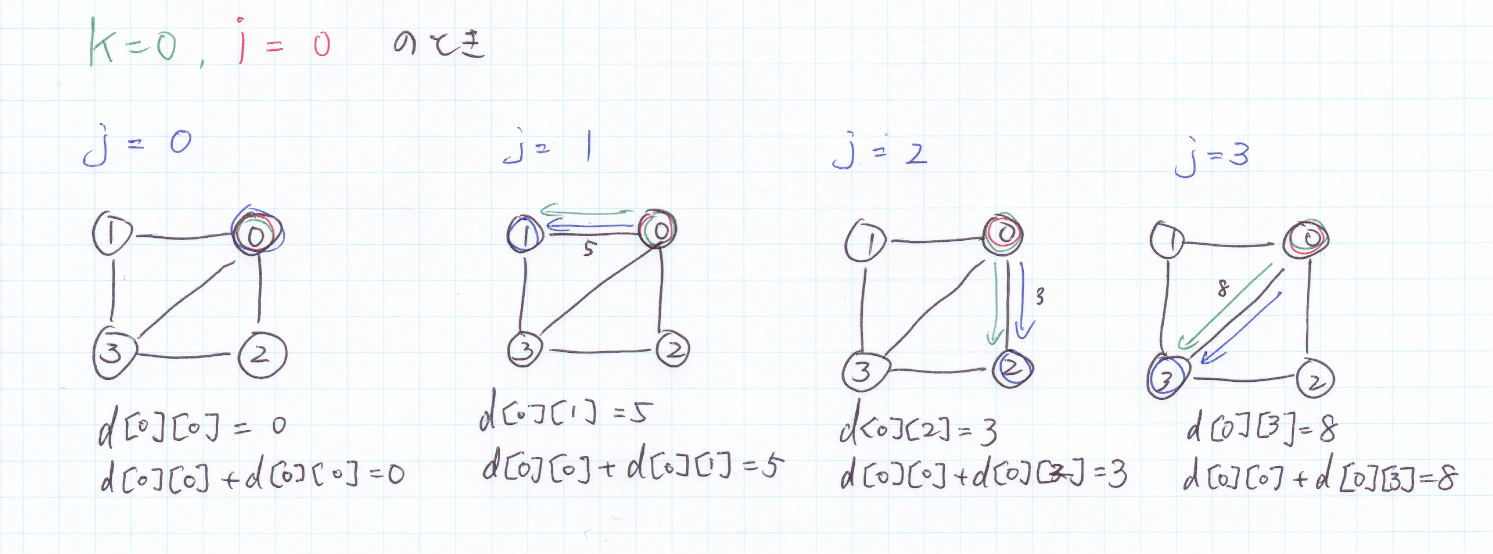
$k = 0, i = 1$のとき
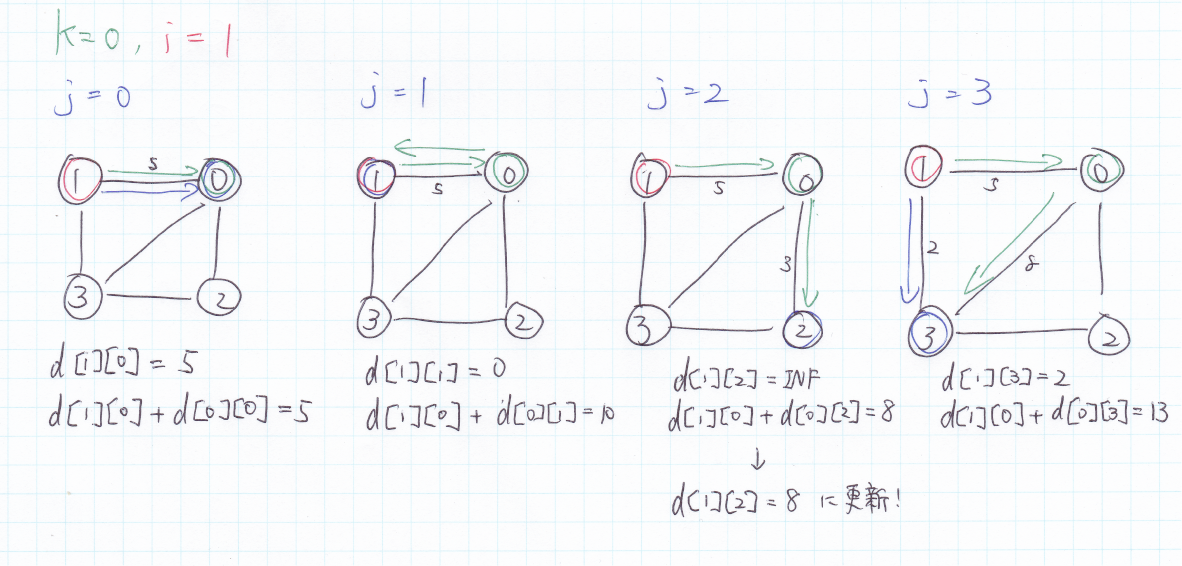
$k = 0, i = 2$のとき
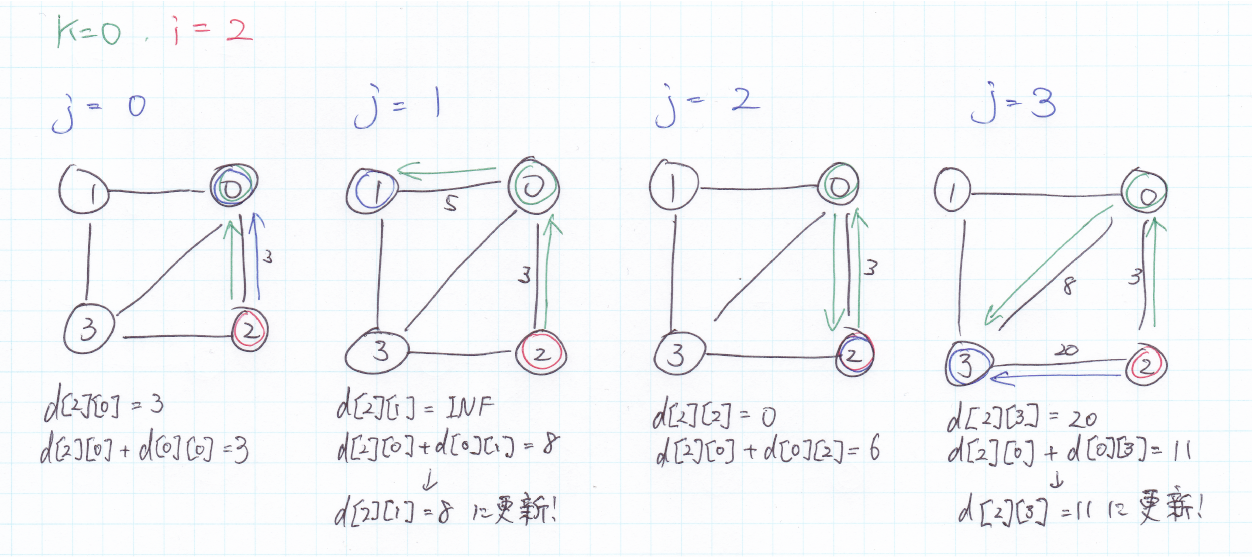
$k = 0, i = 3$のとき
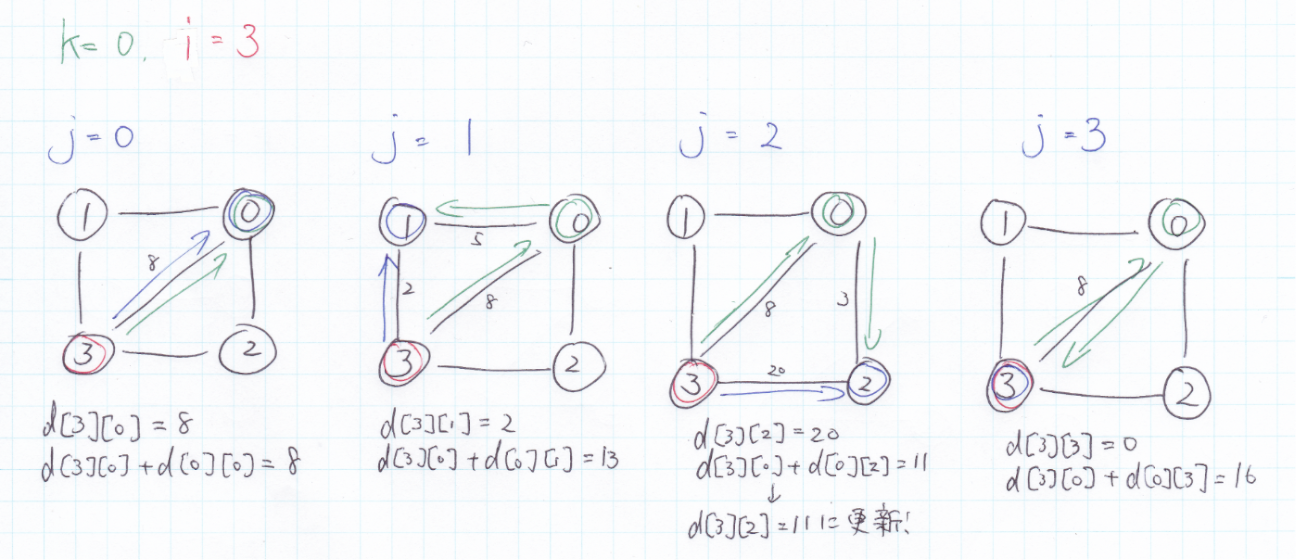
確かに最短経路が更新されている…。でもイマイチ納得できないので別の角度から見てみる。
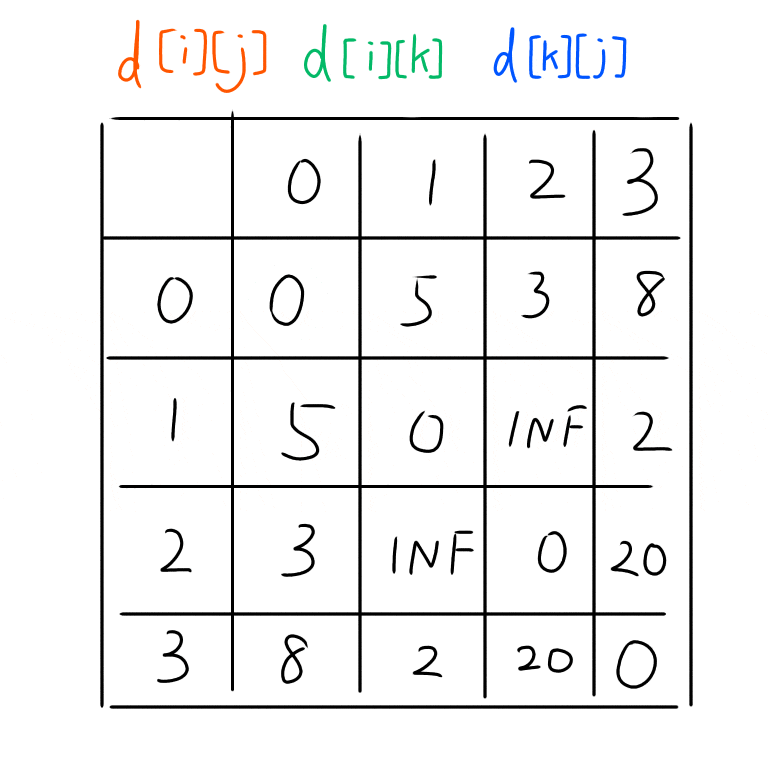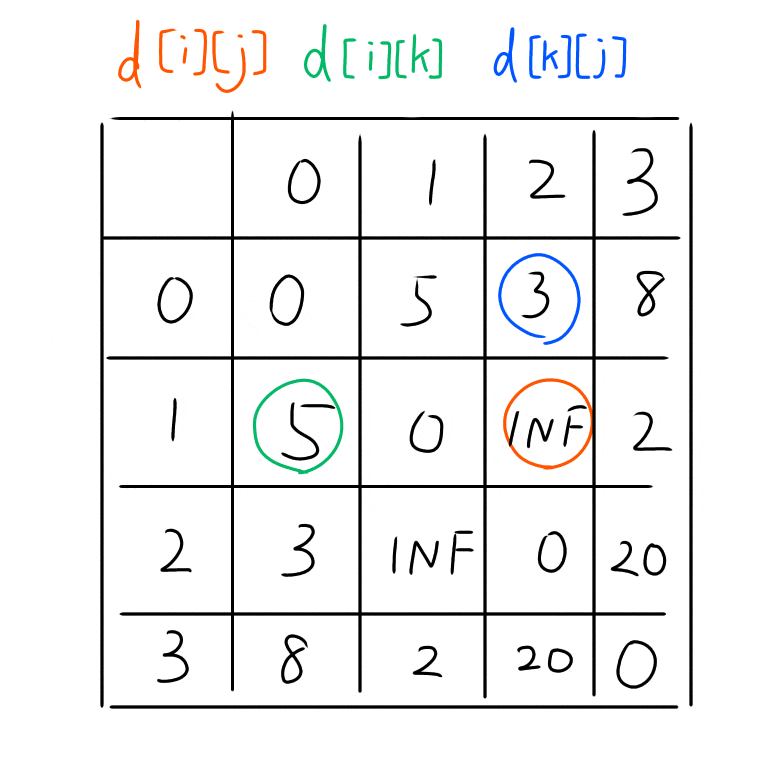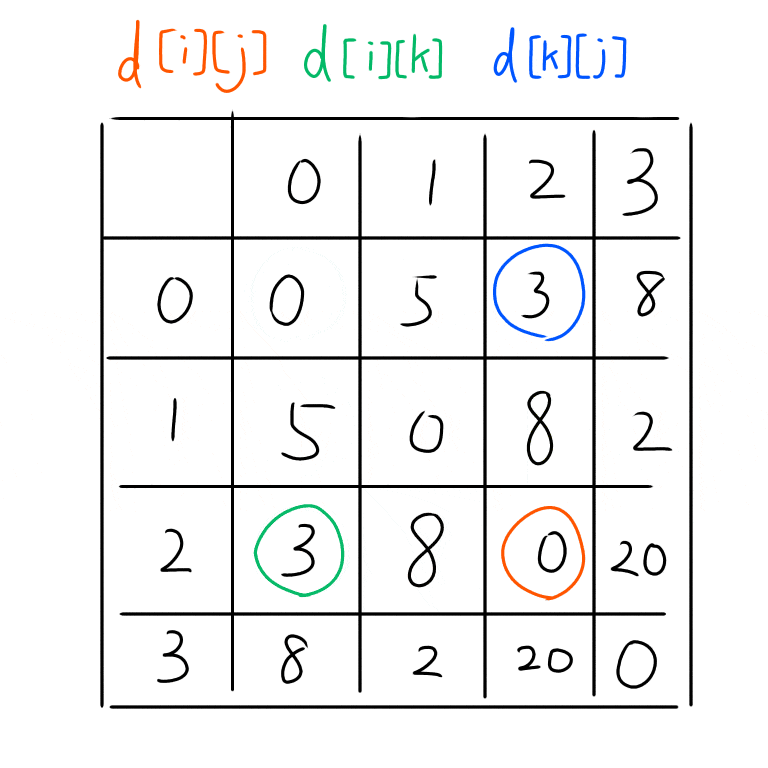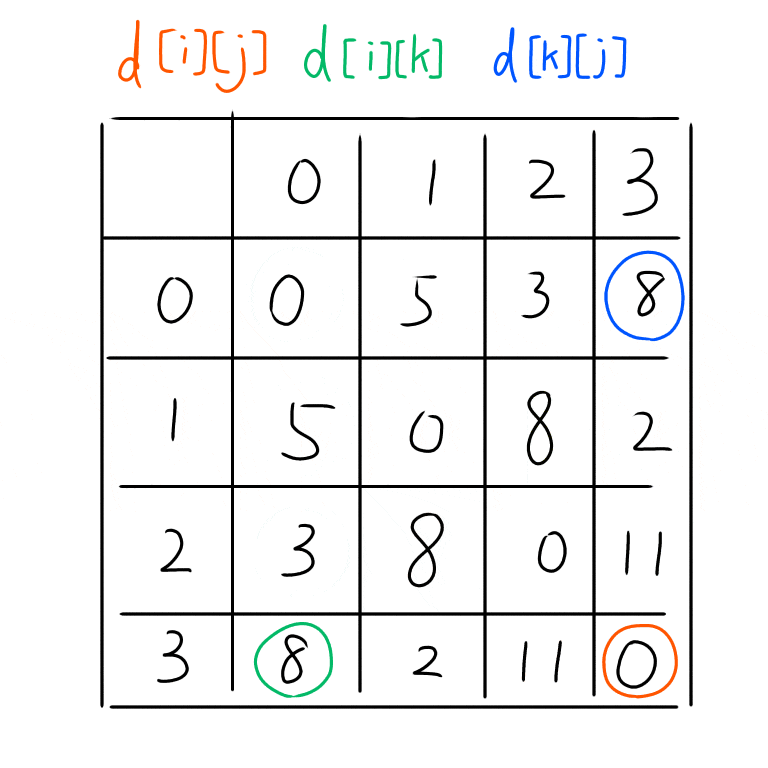
GIF画像を作ってみた。範囲は上の図でやったように$k = 0, i = 0$ から $k = 0, i = 4$の範囲だ。これを見ると規則的に動きながら最短経路が更新されている。
始点、中継地、終点の組み合わせを全部試しながら確かに最短経路を求めている。
おわり
始点、中継地、終点の全探索であるというのは3重ループのあのコードから明らかではあるけれど、あまりに実装が簡単すぎてこれが本当に最短経路を求めるアルゴリズムなのか疑ってしまった。その飲み込みの悪さのためにこんな図まで作ってしまった(もっと要領よくなりたい…)。私と同じようにワーシャルフロイド法をそのまま飲み込みきれず、同じような疑いを持った人がこの記事を読んで理解の助けにしてくれれば今回の私の行為も無駄にならずに済んだと慰めることができるだろう…。
参考文献
『プログラミングコンテスト攻略のためのアルゴリズムとデータ構造』