鍵交換とは
例えば、zipを作成するときにはパスワードを設定しますね。これは、zip作成者がパスワードを知っている人だけが中身を読めるようにするためのものです。
我々がふだん使っているセキュアな通信(TLS, SSHなど)は、送信側と受信側が同じ「鍵」を共有することで行います。実際には鍵は一定の長さのビット列(256ビットがよくありますが、暗号アルゴリズムとその設定でまちまちです)なのですが、送信者と受信者だけが鍵を知っていて、他の人は知らないというのがポイントです。
では、通信を開始するとき、送信者と受信者はどのように鍵を取り決めるのでしょうか? 通信を傍受している悪者がいたとすると、「これからこの鍵で暗号化して通信するよー!」と鍵をそのままネットワークに流しては鍵が悪者にばれてしまい、その後の通信も盗み見ることができてしまいます。しかし通信開始時には暗号化された通信経路は存在しないので鍵が送れなくて困る。これが鍵配送問題です。
謎の風習「パスワードは別のメールで送ります」
皆さんは、仕事で必要なファイルをメールでやりとりする際、パスワードつきzipを添付したメールと解凍パスワードをなぜか別々のメールで送るというのをしたことがある(少なくとも、見聞きしたことはある)と思います。一応、1通のメールだけを見ても中身がわからないという点で、同じメールにパスワードを書くより安全にしたつもりなのかもしれませんが、仮にメールを傍受してzipファイルの中身を盗もうとしている悪者がいれば、当然1通だけでなくすべてのメールを見ているはずなので意味がありませんね。これは単に心理的なものであってセキュリティ上の意味はないのですが、解決しようとしている問題自体はDiffie-Hellmanと一緒なのです。
パスワードは通信ネットワークを使わず、電話で会話したり印刷して郵送したり伝書鳩に届けさせたりすれば、傍受側はネットワークを見るだけでは傍受ができないのでかなり強固な防御策です。しかしこれは手間がかかりすぎます。
鍵交換アルゴリズム
ところが先人には頭のいい人がいるもので、**「傍受されている可能性のある通信ネットワークだけを使い、鍵を安全に相手に届ける」**方法が存在するのです。一見すると魔法のようなトリックですが、数学と計算理論の力を借りて実現できます。この代表例がDiffie-Hellman鍵交換アルゴリズムです。
ふつうの対数
Diffie-Hellmanを理解するには離散対数の理解が必要ですが、その前に普通の対数を復習しておきます。これは高校の数学で出てきますね。
読むのが面倒な人は下の**※印までジャンプ**してもいいです。それでもDiffie-Hellmanは理解できます。
$x ^ y = z$ であるとき、**「xを底としたzの対数はyである」**といいます。
ここで、x と y が与えられている状態で z を求めるにはどうすればいいでしょうか?
コンピュータで計算するときは簡単です。整数同士の掛け算は巨大な整数でも簡単なので、
(1) $x * x$ を計算して $x^2$ を求める。
(2) $(x^2)^2$ を計算して $x^4$ を求める。
(3) $(x^4)^2$ を計算して $x^8$ を求める。
(4) $(x^8)^2$ を計算して $x^{16}$ を求める。
という手順により、n 回の乗算で $x^ {2^n}$ が求まってしまいます。
一方、y は 2のべき数の和で表しておけば、これらの数を使って掛け算で z が求まります。例えば y = 39 だったら、39 = 32 + 4 + 2 + 1 なので、$x^{39} = x^{32} \times x^4 \times x^2 \times x$ という感じです。
今度は、$x$ と $z$ が与えられている状態で $y$ を求めるにはどうすればいいでしょうか? さっきとは分かっている数と求める数が違っています。
でもこれもそれほど難しいことはなく、$x^ {2^n}$ の数をリストした表を用意して、z を超える数が出るまで繰り返して y の範囲を絞り込んでいけばいいので、z が数千ビットであっても数十回の乗算・加算で答えが求まってしまうのです。全然大したことはないのです。
離散対数
ではこれを離散の世界に切り替えます。それは、ある大きな素数 p を用意して、「p で割った余り」で演算していくということです。
では $x ^ y = z \ mod \ p$ とします。ここで、さっきと同様に$x, y, p$ が与えられているときに $z$ を求めるにはどうすればいいでしょうか?
これも手順は一緒で、
(1) $x * x$ を計算して $x^2 \ mod \ p$を求める。
(2) $(x^2 \ mod \ p)^2$ を計算して $x^4 \ mod \ p$を求める。
(3) $(x^4 \ mod \ p)^2$ を計算して $x^8 \ mod \ p$を求める。
(4) $(x^8 \ mod \ p)^2$ を計算して $x^{16} \ mod \ p$を求める。
というようにしてガンガン計算表を作ることができます。
事態が一変するのはここから。$x, z, p$が与えられているときに y を求めるのはどうしたらいいでしょうか? これは計算理論の分野なので説明は省略しますが、**「p が大きな素数のときは非常に難しい」**のです。ここが離散ならではの特徴です。
ここで重要な性質を確認します。
※ $x^y = z \ mod \ p$ (p は大きな素数) のとき
(x,y,p)からzを求めるのはカンタン。(x,z,p)からyを求めるのは困難。
ここで困難というのは不可能という意味ではないことに注意してください。じっくり計算すれば答えは出るのですが、前者はスマホでも一瞬で答えが出るのに、後者は高価なコンピュータを何年もブン回す必要がある、というような計算量の非対称性があるのです。
Diffie-Hellman
ここでやっと本題です。
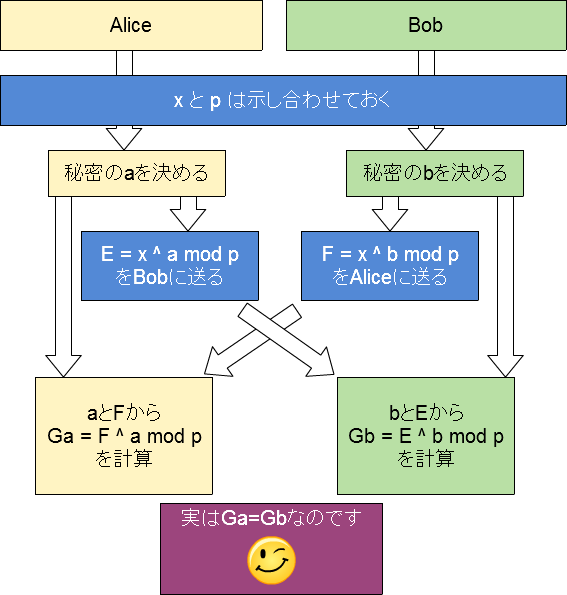
いま、AliceとBobの2人がDiffie-Hellmanを使って鍵交換をしようとします。次のステップになります。
(1) 大きな素数 $p$, 小さな適当な整数 $x$ を用意しておく。これは公開して構わない。
(2a) Aliceが秘密の $a$ を, 2 以上 $p$ 未満の整数からランダムに選ぶ。
(3a) Aliceは $E = x^a \ mod \ p $ を計算する(これがカンタンなことはさっき確認しました)。その結果の $E$ をBobに送る。
(2b) Bobが秘密の $b$ を, $2$以上 $p$ 未満の整数からランダムに選ぶ。
(3b) Bobは $F = x ^ b \ mod \ p$ を計算する(これがカンタンなことはさっき確認しました)。その結果の $F$ をAliceに送る。
(4a) Aliceは、Bobから受け取った $F$ と、自分の手元にある $a$ を使って、 $Ga = F ^ a \ mod \ p$ を計算する。
(4b) Bobは、Aliceから受け取った $E$ と、自分の手元にある $b$ を使って、 $Gb = E ^ b \ mod \ p$ を計算する。
さてこの結果、E と Fを求めたときの手順を見れば、$Ga = Gb = (x ^ {ab} ) \ mod \ p$ であることがわかります。これをAliceとBobの共通鍵にすればいいのです。
仮にこの通信を傍受している悪者がいたとしても、見えるのは $x, p, E, F$ のみです。そこから $a$ や $b$ を逆算するのが困難であるのはさきほど確認したとおりです。
SSHの場合
申し遅れましたが、私はPoderosaというSSHクライアントを開発しており、SSHプロトコルには実はけっこう詳しいのです。昔に未踏ソフトウェア事業に採択もされましたが、その後放置期間を経て2016年に復活しました。
SSHでは、この計算において x = 2 で固定された値を使っています。pについては、16進数で
FFFFFFFFFFFFFFFFC90FDAA22168C234C4C6628B80DC1CD129024E088A67CC74020BBEA63B139B22514A08798E3404DDEF9519B3CD3A431B302B0A6DF25F14374FE1356D6D51C245E485B576625E7EC6F44C42E9A637ED6B0BFF5CB6F406B7EDEE386BFB5A899FA5AE9F24117C4B1FE649286651ECE65381FFFFFFFFFFFFFFFF
(diffie-hellman-group1-sha1)
という値が長らく使われてきましたが、最近はこの程度では計算機パワーで力ずくで解けてしまう危険が高まったのでさらに大きな
FFFFFFFFFFFFFFFFC90FDAA22168C234C4C6628B80DC1CD129024E088A67CC74020BBEA63B139B22514A08798E3404DDEF9519B3CD3A431B302B0A6DF25F14374FE1356D6D51C245E485B576625E7EC6F44C42E9A637ED6B0BFF5CB6F406B7EDEE386BFB5A899FA5AE9F24117C4B1FE649286651ECE45B3DC2007CB8A163BF0598DA48361C55D39A69163FA8FD24CF5F83655D23DCA3AD961C62F356208552BB9ED529077096966D670C354E4ABC9804F1746C08CA18217C32905E462E36CE3BE39E772C180E86039B2783A2EC07A28FB5C55DF06F4C52C9DE2BCBF6955817183995497CEA956AE515D2261898FA051015728E5A8AACAA68FFFFFFFFFFFFFFFF
(diffie-hellman-group14-sha1)
というものも使われています。世の中のほとんどすべてのSSH接続では、ログイン時にこのどちらかの p を使っているのです。この巨大素数は世界共通の資産といえます。
まとめ
- Diffie-Hellman鍵交換は、傍受されている通信路を使っても安全に通信相手に鍵を届けることができる
- その根拠は、 $x ^ y = z \ mod \ p$ (p は大きな素数) において、(x, y, p)から zを求めるのは簡単だが(x, z, p)からyを求めるのは困難という計算理論上の定理である
穴
Diffie-Hellman鍵交換が担当するのはあくまでも通信の傍受に対する耐性です。セキュリティにおいては別の問題もいろいろあるので、決して万能ではありません。例えば、Aliceが通信 している相手はBobではなく「Bobのふりをした悪者」だった場合は極めて危険です。
また、計算理論の定理も将来は崩される危険があります。量子コンピュータのような、これまでとは次元の異なる計算手段が実用化された場合、一発で前提がひっくり返る可能性があります。その確率はとても低いですが、0ではありません!