Juliaで厳密対角化！（S=1/2の量子スピン系）

こんにちは。
スピン1/2の量子スピン鎖をJuliaで厳密対角化してみようと思います。
備忘録として公開します。
ここではHeisenberg模型を例にあげます。つまり

H = J\sum_{i=1}^{N-1}\vec{S}_i\cdot\vec{S}_{i+1}

で定義されるようなハミルトニアンです。$S=1/2$の場合、$S_i^\alpha = (\hbar/2)\sigma_i^\alpha~~~ (\alpha = x,y,z)$という関係があります。
ここではパウリ行列$\sigma_i^\alpha$を

\begin{align}
\sigma^x=\pmatrix{0 & 1 \\ 1 & 0}, \\
\sigma^y=\pmatrix{0 & -i \\ i & 0}, \\
\sigma^z=\pmatrix{1 & 0 \\ 0 & -1}.
\end{align}

として、$H=\frac{J}{4}\sum_{i=1}^{N-1} (\sigma_i^x\sigma_{i+1}^x+\sigma_i^y\sigma_{i+1}^y+\sigma_i^z\sigma_{i+1}^z)$として考えることにします。$J,\hbar$はどちらも$1$としておきます。ここで、$\sigma_i^\alpha$は以下のクロネッカー積の略記です。

\sigma_i^\alpha = 1\otimes1\otimes\cdots\otimes\underbrace{\sigma^\alpha}_{i\textrm{番目}}\otimes\cdots\otimes 1

$1$は$2\times 2$の単位行列です。

クロネッカー積を用いた表現

例として$N=2$の場合を考えます。

const x = [0 1;
        1 0]
const y = [0 -im;
        im 0]
const z = [1 0;
        0 -1]

⊗=kron
function make_ham()
    return (x⊗x+y⊗y+z⊗z)/4
end

これでハミルトニアンを作ることができました。
出力してみると次のようになります。

H = make_ham()
display(H)

###出力###
#4×4 Matrix{Complex{Int64}}:
# 1+0im   0+0im   0+0im  0+0im
# 0+0im  -1+0im   2+0im  0+0im
# 0+0im   2+0im  -1+0im  0+0im
# 0+0im   0+0im   0+0im  1+0im

ちょっと工夫したい

上の例で出力された行列をみると、ブロック対角になっています。
固有値の計算をする際には行列次元はできるだけ小さい方が嬉しいので、最初からブロック対角化された部分を取り出したいと思います。

実際このハミルトニアンは以下の交換関係を満たしています。

[H,S_\textrm{tot}]=HS_\textrm{tot}-S_\textrm{tot}H=0

ここで、$S_\textrm{tot}=\sum_{i=1}^{N-1}S_i^z$です。
したがって、同時対角化可能なので$S_\textrm{tot}$の固有値のよってブロック対角できることになります。
通常の量子力学でやるような記法を用いて、$\sigma^z$の固有状態を$\ket{\uparrow},\ket{\downarrow}$として、考えましょう。それぞれ固有値は$+1,-1$になります。例えば2個の量子スピンならば$\ket{\uparrow,\downarrow}=\ket{\uparrow}\otimes\ket{\downarrow}$のように表記します。

$N=2$の場合には、$\ket{\uparrow, \downarrow}, \ket{\downarrow,\uparrow}$の2つを基底にすることで$S_\textrm{tot}=0$の部分を表すことができます。

考え方としてはハミルトニアンを

H = \frac{1}{8}\sum_{i=1}^{N-1}(\sigma_i^+\sigma_{i+1}^--\sigma_{i}^-\sigma_{i+1}^++2\sigma_{i}^z\sigma_{i+1}^z)

のように変形できることを用います。ここで、$\sigma_i^\pm = \sigma_i^x\pm\sigma_i^y$です。

\begin{align}
\sigma^+\ket{\uparrow}&=0 \\
\sigma^+\ket{\downarrow}&=\ket{\uparrow}\\
\sigma^-\ket{\uparrow}&=\ket{\downarrow} \\
\sigma^-\ket{\downarrow}&=0
\end{align}

のように基底に作用します。
これらを用いてハミルトニアンを作りたいと思います。

2進法表記

スピン1/2をfalseが$\ket{\uparrow}$、trueが$\ket{\downarrow}$となるようにBoolで定義しましょう。これには2進法を使うのが便利です。
例えば$\ket{\uparrow\downarrow\uparrow}$を$\ket{010}$として、10進法では2だと考えるようにします。

以下のコードは一部こちらの記事を参考にしました

i_to_state(i,N)という関数で10進法を2進法にしてBool型のリストにしています。

mutable struct Spinbasis{N}
    state::Array{Bool,1}
    index::Int64
    function Spinbasis(N, index)
        state = i_to_state(index, N)
        return new{N}(state, index)
    end
end

function i_to_state(i, N)
    @assert 0 <= i < 2^N
    state = zeros(Bool, N)
    bit = string(i, base=2, pad=N)
    for i = 1:N
        state[i] = parse(Bool, bit[i])
    end
    state
end

これをケットで表記させたいのでBase.display(spin::Spinbasis{N})を定義します。

function Base.display(spin::Spinbasis{N}) where {N}
    label = get_label(spin)
    println(label)
    return
end

function get_label(spin::Spinbasis{N}) where {N}
    label = ""
    label *= "|"
    for i = 1:N
        if spin.state[i]
            label *= "↓"
        else
            label *= "↑"
        end
    end
    label *= ">"
end

こうすることで、例えば

N = 3
i = 2
state = Spinbasis(N, i)
display(state)
###出力
#|↑↓↑>

とできます。

ブロック対角

各基底に対して、$S_\textrm{tot}$を計算します。
spin.spins(spin::Spinbasis{N})は基底を入力するとそれに対して$S_\textrm{tot}$を出力する関数で、以下のように表せます。spin.stateはBool型のリストであることに注意してください。

function sum_spins(spin::Spinbasis{N}) where {N}
    stot = 0
    for i = 1:N
        if spin.state[i]
            stot -= 1 / 2
        else
            stot += 1 / 2
        end
    end
    return stot
end

では$S_\textrm{tot}=s$となるようなindex（10進法表記した場合の添え字）を取り出してみましょう。nsiteはサイト数$N$で、stotが$s$に対応します。
$2^N$個の基底に対してsum_spins(state)≈stotかどうかを見ています。
最終的に$S_\textrm{tot}=s$となるようなインデックスのリストを出力します。

function index_stot(nsite, stot)
    id_max = 2^nsite
    index_list = []
    for i in 1:id_max
        state = Spinbasis(nsite, i - 1)
        if sum_spins(state) ≈ stot
            push!(index_list, state.index)
        end
    end
    return index_list
end

ハミルトニアンの構成

だいぶ長くなってきましたが、もう少しでハミルトニアンを構成できます。
次に$\sigma_i^\pm/2$によって基底を更新させることを考えます。対応するコードは以下の通りで、
upspin!によってisite番目の$\ket{\downarrow}$を$\ket{\uparrow}$にします。
downspin!はその逆です。
state_to_iは状態を更新するときにstate.indexを更新するために使います。

function state_to_i(state)
    N = length(state)
    ii = 0
    for i = 1:N
        ii += state[N-i+1] * 2^(i - 1)
    end
    return ii
end

function upspin!(spin::Spinbasis{N}, isite) where {N}
    @assert check_up(spin, isite) "The spin is already up at $(isite)-site!"
    spin.state[isite] = false
    spin.index = state_to_i(spin.state)
end

function downspin!(spin::Spinbasis{N}, isite) where {N}
    @assert !check_up(spin, isite) "The spin is already down at $(isite)-site!"
    spin.state[isite] = true
    spin.index = state_to_i(spin.state)
end

これにより$S_i^+S_j^-=\sigma_i^+\sigma_j^-/4$と$S_i^zS_j^z=\sigma_i^z\sigma_j^z$を次のように作ることができます。
ここではデフォルトでstot = 0としています。
ndimは行列次元で、length(index_list)と表せます。
この値は組み合わせを用いて、

\textrm{ndim}={}_{N}\textrm{C}_{(N+s)/2}

とも表せます。
for文でenumerateを使っているのは行列の成分を表す添え字がはindexではないからです。

function make_SpSm(isite, jsite, nsite, index_list, ndim, stot=0)
    mat = zeros(Int64, ndim, ndim)
    for (iind, index) in enumerate(index_list)
        spin = Spinbasis(nsite, index)
        if !check_up(spin, jsite) && check_up(spin, isite)
            downspin!(spin, jsite)
            upspin!(spin, isite)
            jindex = spin.index
            jind = findfirst(x -> x == jindex, index_list)
            mat[jind, iind] = 1
        end
    end
    return mat
end

function make_SzSz(isite, jsite, nsite, index_list, ndim, stot=0)
    mat = zeros(Float64, ndim, ndim)
    for (iind, index) in enumerate(index_list)
        spin = Spinbasis(nsite, index)
        sign = 1
        if !check_up(spin, isite)
            sign *= -1
        end
        if !check_up(spin, jsite)
            sign *= -1
        end
        mat[iind, iind] = sign / 4
    end
    return mat
end

以上の準備を終えて、ハミルトニアンを作る関数make_Ham(nsite, stot)を作ることができました。

function make_Ham(nsite, stot)
    index_list = index_stot(nsite, stot)
    ndim = length(index_list)
    mat = zeros(Float64, ndim, ndim)
    for i in 1:nsite-1
        mat += make_SpSm(i, i + 1, nsite, index_list, ndim)
        mat += make_SzSz(i, i + 1, nsite, index_list, ndim)
    end
    mat += mat'
    mat = mat / 2
    return mat
end

対角化してみる

実際にLinearAlgenbraを用いて対角化してみましょう。

using LinearAlgebra
nsite = 4
stot = 0
H = make_Ham(nsite, stot)
e, v = eigen(H)
println("基底状態のエネルギーは$(e[1])です。")

index_list = index_stot(nsite, stot)
for (i, v) in enumerate(v[:, 1])
    if v > 0
        print("+")
    end
    print(v)
    display(Spinbasis(nsite, index_list[i]))
end

###出力
#基底状態のエネルギーは-1.616025403784435です。
#-0.14942924536134217|↑↑↓↓>
#+0.5576775358252046|↑↓↑↓>
#-0.40824829046386296|↑↓↓↑>
#-0.4082482904638628|↓↑↑↓>
#+0.5576775358252059|↓↑↓↑>
#-0.1494292453613427|↓↓↑↑>

上の例は$N=4$ですが、ちゃんと対角化することができ、基底状態を求めることができました。

（おまけ）どのくらい次元を減らせているのか

元々の行列次元は$2^N$でした。例えば$N$が偶数で、$S_\textrm{tot}=0$となる場合には行列次元は

{}_N\textrm{C}_{N/2}

となっているので、
次元は

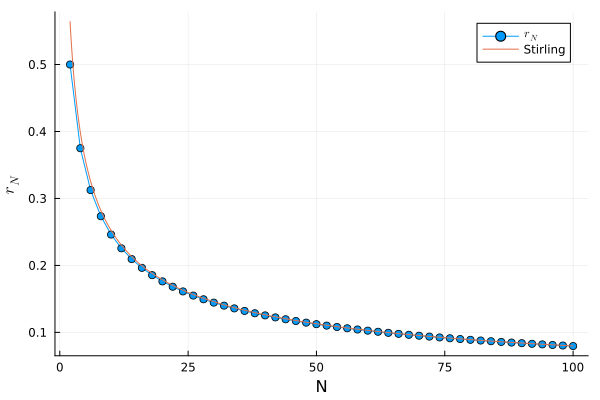
r_N = \frac{{}_N\textrm{C}_{N/2}}{2^N}

だけ小さくなっています。
スターリングの公式

n!\sim \sqrt{2\pi n}\left(\frac{n}{e}\right)^n 

を用いると十分大きな$N$に対しては、

r_N \sim \sqrt{\frac{2}{\pi N}}

となることを示せます。
実際、この比$r_N$は以下のようになっています。