擬似量子アニーラで相関係数に基づく特徴量選択を行う

はじめに（何をしたいか）

タイトルの通り、この記事では、擬似量子アニーラを用いて、相関係数に基づく特徴量を選択する方法について、説明します。

擬似量子アニーラ

擬似量子アニーラとは、もって回った言い方になりますが、「『量子コンピュータの実現手法として提唱された断熱量子計算モデルの実装である量子アニーラ』を半導体技術で再現したもの」を指します。過去にも、別の記事でアニーリングマシンに触れていますので、詳しくは、そちらを読んでください。
https://qiita.com/ojiya/items/e6741a18abac265f8318

結局どう使うのか

現実の問題を、QUBO、つまりは二値変数の二次式の形式に落としこんで、それを解くことによって、現実の問題への近似解を得る、というのが基本的な考え方です。難しいのは、そんなに都合よく現実の問題がQUBOに変換できない、ということなのですが、最近では、いろいろと変換のしようはあることがわかってきています。応用物理学会なんかで、ちょいちょい発表があります。

この記事ではどう使うのか

この記事では、相関係数に基づいた特徴量の削減を、擬似量子アニーラで実装します。「相関係数に基づいた特徴量の削減」そのものについては、いろんなところで解説されているのでここでは特に解説しませんが、例えば、下記の記事のような内容です。
https://data-anal-ojisan.com/2021/10/13/791/

意味はあるのか

あんまりないです。ただ、擬似量子アニーラも使い慣れてくると、サッと実装できるようになるので、それを実感してもらえたらな、と思います。
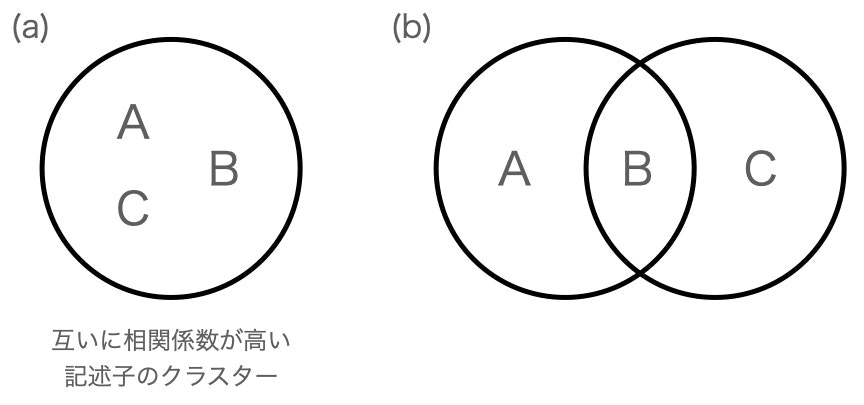
とはいえ、一つだけこの問題を擬似量子アニーラで解くメリットもあるにはあるので、一応述べておきます。上記で紹介した特徴量削減についての記事もそうなのですが、相関係数に基づいて特徴量を削減するとき、往々にして、「特徴量テーブルの順番」で、結果が変わるような実装をしてしまいがちです。例えば、下図の(b)のようなシチュエーション（丸で囲われた特徴量同士は、互いに相関係数が高いとする）では、特徴量Aがテーブルの前に来ている時、Bは削除され、Cは残ります。他方、Bが最初に来ていれば、AとCは消えます。「特徴量テーブルの並び順」という、本来は全く意味を持たないものによって結果が左右されるのは大変気持ち悪いのですが、擬似量子アニーラは、「どの特徴量を採用し、どれを使わないか」を一括で決めるので、このような問題は起きません。まぁ、些細な問題ではありますが、、、

（出典：https://qiita.com/ojiya/items/a867b8b1906e18a264a8）

実装

ハミルトニアンの設計

天下り的ですが、下記のようなハミルトニアンを考えます。

H=Q_{corr}\sum_{|r_{ij}|\geq r_0}{q_iq_j}+Q_{n}\sum_iq_i

ここで、$q_i$は、「ある特徴量$x_i$を残すか残さないか」を表しており、$q_i=1$なら特徴量を残しす、$q_i=0$なら削除します。また、$r_{ij}$は特徴量$x_i$と$x_j$の相関係数、$r_0$は相関係数の閾値を表します。従って、第一項は、「相関係数の絶対値が閾値より高い場合、ハミルトニアンを増加させるような効果が発生する」ことを意味します。第二項は、全ての$q_i$が0になることを防ぐための項です。第一項だけの場合、「全ての$i$について$q_i=0$」という自明でつまらない解に落ちてしまうのですが、第二項により、これを防いでいます。従って、$Q_n$は小さな負の値です。
実装の際の説明のしやすさを考えて、少し第一項をいじった形も示しておきます。

Q_{corr}\sum_{|r_{ij}|\geq r_0}{q_iq_j}=\sum_{|r_{ij}|\geq r_0}{Q_{ij}q_iq_j}

$Q_{ij}$は、係数行列$\boldsymbol{Q}$の、第$ij$成分です。コーディングでハミルトニアンを作るとは、この行列$\boldsymbol{Q}$を作ることと同義です。

実装するためのコード

ここでは、Fixstars Amplifyの開発している、amplifyを用います。APIなどは、適宜取得して下さい。
https://amplify.fixstars.com/ja/

上記で紹介した https://data-anal-ojisan.com/2021/10/13/791/ を真似してデータテーブルを作っていきます。ここまでは、特に解説すべきことはないです。

# 基本のライブラリ
import pandas as pd 
import numpy as np 
# データ取得
from sklearn.datasets import load_breast_cancer
#擬似量子アニーラ
from amplify import FixstarsClient,VariableGenerator,solve
client = FixstarsClient()
client.token = '自分のトークンを入れる'

# サンプルデータのインスタンスを生成
cancer = load_breast_cancer()

# 特徴量をデータフレームに変換
X = pd.DataFrame(cancer.data,
                 columns=cancer.feature_names)

print(X.shape)
display(X)

ちなみに、相関係数の可視化などは、この記事では省略しています。擬似量子アニーラの実装に注目したいからです。
次がメインの部分です。先に述べたように、係数行列$\boldsymbol{Q}$を作っていきます。まず、相関係数を成分にもつ行列を計算します。

# 相関係数の行列を作成
X_corr = X.corr()

次がキモです。わかれば単純なのですが、多分、最初は「？」です。$\boldsymbol{Q}$の非ゼロの項は、特徴量$x_i$と$x_j$の相関係数が高いところ、つまりは「上記で計算したX_corrの成分の絶対値が閾値よりも高い$i$、$j$のペア」です。また、今考えているのはQUBOの二次の項なので、「対角成分（=相関係数が1のところ）は除外」します。従って、$\boldsymbol{Q}$は、次のように作ることができます。

# 閾値よりも値が高い部分を1としたものが、そのままQ_corrになる
corr_threshhold = 0.95
Q_high_corr = np.array((X_corr!=1)*(np.abs(X_corr)>=corr_threshhold)).astype(int)

続いて、第二項を実装します。こっち対角項が全て1の行列（要するに単位行列）なので、サイズだけ気にすればいいですね。

# すべてのqが0にならないようにする
Q_size = arr_high_corr.shape[0]
Q_n = np.eye(Q_size)

あとは、お決まりの表現が続くので、一気に書いてしまいます。係数をかけて全体の行列にしたあと、決まった記法に従ってamplifyの入力形式に変換し、問題を解いて、特徴量の必要なところだけを取り出します。

# 係数行列を組み合わせる
coef_Q_high_corr = 1
coef_Q_n = -0.01
Q_total = coef_Q_corr*Q_high_corr + coef_Q_n*Q_n

# amplifyの入力形式にする
gen = VariableGenerator()
m = gen.matrix("Binary", shape=Q_size)
m.quadratic = np.triu(Q_total)
q = m.variable_array

# 解く
n_solve = 1
# 最適化にかける時間を設定
client.parameters.timeout = 3000
result = solve(m, client, num_solves=n_solve)

# 解を元に、特徴量を取り出す
sol = result.solutions[0]
solution = sol.values
arr_result = q.evaluate(solution)

mask_result = arr_result.astype(bool)
X_drop_corr = X.loc[:,mask_result]

最後に、相関係数の高いペアがちゃんと落ちたことを確認します。

chk_corr = X_drop_corr.corr()

np.array((chk_corr != 1)*(np.abs(chk_corr)>=corr_threshhold)).any()

これで出力がFalseなら成功です。

おしまい。