Starry DataとXenonpyで意識の低いマテリアルズインフォマティクスをする② 記述子を削減する

はじめに

この記事で書くこと

この記事は、以下の記事の続きである。

上の記事に書いたように、意識の低いマテリアルズインフォマティクスをやりたい。この記事では、前回作成した記述子を減らして、回帰や予想に必要なものを抽出していく。実のところ、これには決まったやり方があるわけではないのだが、この記事で書くようなことは、多くの場合に、やっておいて損はない。と思う。

この記事で使うもの

・Starry Data 2
東京大学の桂ゆかり先生( https://twitter.com/nezdenmama )のStarry Dataプロジェクトからデータを持ってくる。アクセスしてみればわかるが、ものすごいデータ量である。内容の信頼性も高いので、これからデータ科学的に材料化学データを扱いたい人にはもってこいのデータベースである。
https://sites.google.com/site/yukarisearch/starrydata

・Xenonpy
統計数理研究所吉田研究室で開発されている。このページに辿り着いている時点で、Xenonpyがなんなのか把握していると思うので、説明は省く。

データを読み込む

前記事の最後に書いておけばよかったのだが、下記のコードを使って、作成した記述子を保存しておいたことにする。

pd.concat([prop, descriptor], axis=1).to_csv('prop_desc.csv', index=None)

ここで作成したファイルを読み込めば、前回の続きから解析を始めることができる。上のコードを見てわかるように、一列目に目的変数（prop）、それ以降の列に記述子（descriptor）が書いてある。目的変数の列名は、'log_ed'となっているので、目的変数を読み込むときは、'log_ed'列のみを取り出し、記述子を読み込むときは、'log_ed'列を落としている（.drop('log_ed', axis=1)）。出力結果は省略。

import pandas as pd

#読み込んで、目的変数と記述子に分離
prop = pd.read_csv('prop_desc.csv')['log_ed']
desc = pd.read_csv('prop_desc.csv').drop('log_ed', axis=1)
desc.head()
#出力は記述子のデータフレームの先頭5行

明らかに役に立ちそうにない記述子を削除する

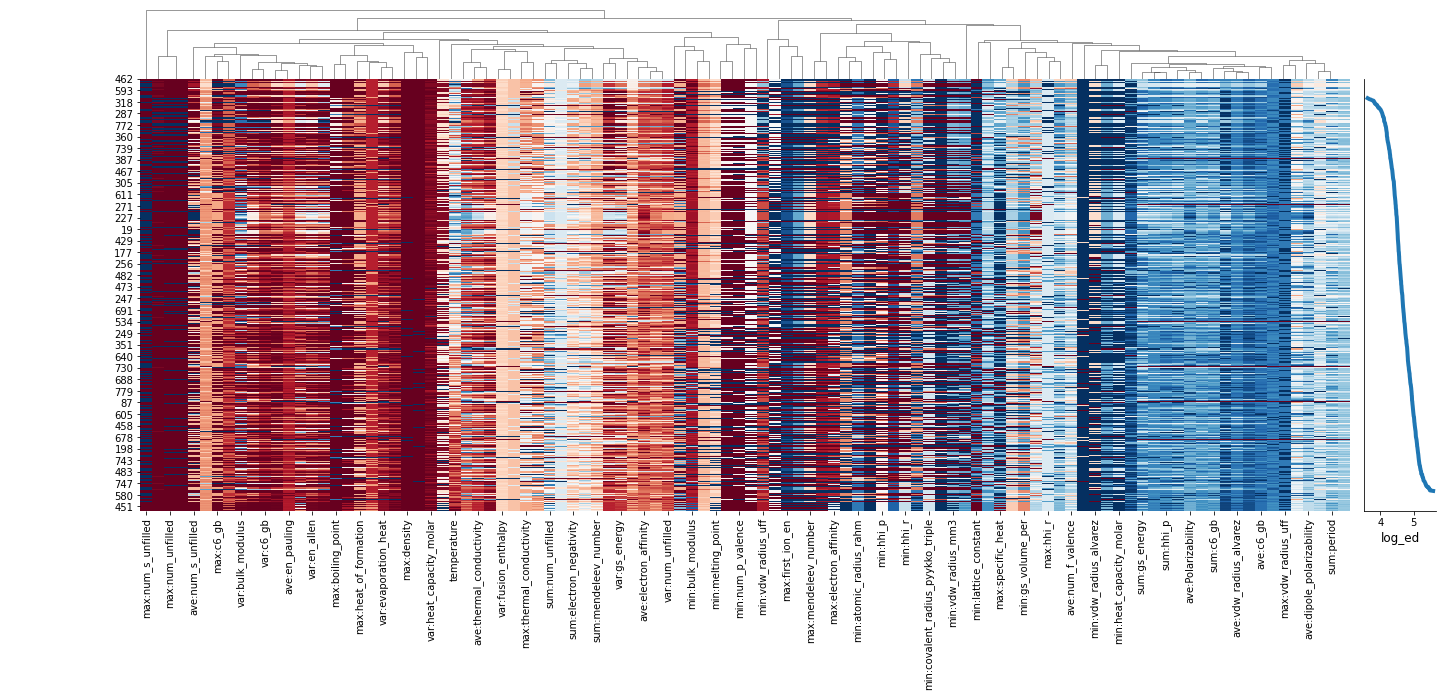
さて、以下には、前回も示したヒートマップを示した。パッと見で、
・全く値が変化しない記述子がある（真ん中少し左の赤い領域）
・目的変数に対して全く同じ依存性を与える記述子がある
ということがわかる。まずは、このあたりに手を入れていこう。

値が一定の記述子を削除する

このような記述子が役に立たないことについては、説明不要と思う。各記述子の最大と最小が一緒な場合は削除する、という操作をすればいいので、以下のループを回す。内包表記でもいいのだが、後の都合により、forループにしている。また、desc.drop(drop_col, axis=1)とすれば、これらの列を落とした記述子が手に入る。

#列名をループの基準にする
col_names = desc.columns
#削除する記述子を入れる、drop_colを作成する
drop_col = []

#minとmaxが同じ（==）ものは、drop_colに入れていく
for col_name in col_names:
    if min(desc[col_name]) == max(desc[col_name]):
        drop_col.append(col_name)

#内包表記の場合は、以下の通り
#drop_col = [col_name for col_name in col_names if min(desc[col_name]) == max(desc[col_name])]

print(drop_col)
#以下の行を実行すれば、desc_0には、drop_colに入れた記述子が削除できる
#desc_0 = desc.drop(drop_col, axis=1)

#出力結果
#['ave:gs_mag_moment', 'ave:num_d_unfilled', 'ave:num_f_unfilled',
#'sum:gs_mag_moment', 'sum:num_d_unfilled', 'sum:num_f_unfilled', 
#'var:gs_mag_moment', 'var:num_d_unfilled', 'var:num_f_unfilled', 
#'max:gs_mag_moment', 'max:num_d_unfilled', 'max:num_d_valence', 
#'max:num_f_unfilled', 'max:num_f_valence', 'max:num_s_valence', 'max:period', 
#'min:gs_bandgap', 'min:gs_mag_moment', 'min:num_d_unfilled', 'min:num_f_unfilled', 
#'min:num_f_valence', 'min:num_s_unfilled']

相関係数を使って記述子を削除する

相関係数が高い記述子同士は、目的変数に似たような依存性を与える。互いに相関係数が高い記述子同士が含まれた状態で解析を行うと、おかしな結果が出てくる可能性がある。ここでは触れないが、「多重共線性」などでググると、いろいろと解説が出てくると思う。このような問題を回避する作用が組み込まれているアルゴリズムもあれば、そうでないアルゴリズムもある。これからアルゴリズムを選択していこう、という場面で、「でも、このアルゴリズムは多重共線性の問題を回避できないから、、、」みたいな制約に見舞われるのはあまり嬉しくないので、先に対策をしておこう。

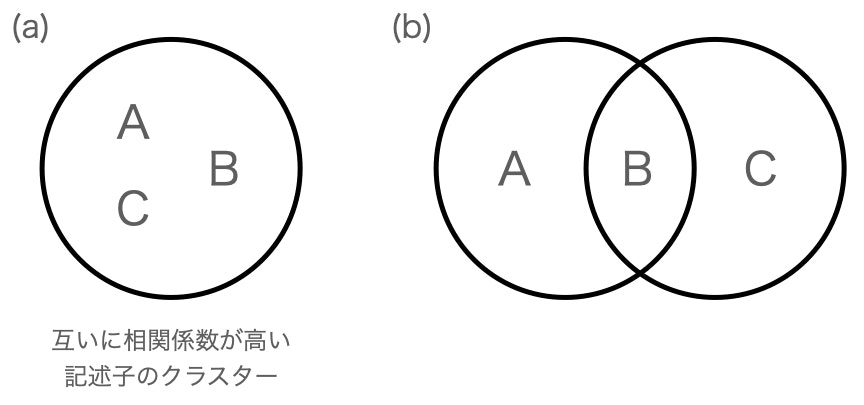
単純に考えると、相関係数の高い記述子同士のペアから、片一方を消していけばいい、というのが基本的な考え方だ。ただし、少し考えると、例えば「記述子Aと記述子Bの相関係数が大きく、記述子Bと記述子Cの相関係数が高い」場合、「記述子Aと記述子Cも相関係数が高い」可能性がある（下図(a)）。つまり、相関係数の高い記述子同士でクラスターを作っていると予想できる。じゃあ、クラスターを調べて、その中から任意の記述子を選べばいいか、というと、そうでもない。上の予想とは逆に、「記述子Aと記述子Cの相関係数は高くない」という場合も、当然ありうるからだ（下図(b)）。このような場合には、記述子Bを選べば、効率的に記述子の数を減らしていくことができるだろう。では、ここでいう「記述子B」を探すにはどうしたら良いだろうか。

ここでは、簡単なやり方として、「自分と相関係数が高い記述子の数」が多い記述子を取り出すことで、「記述子B」に相当する記述子を抽出することにする。上の例では、AやCでは1つずつ、Bでは2つである。他にも、相関係数の合計が大きいものを採用する、というやり方もあるらしい。ここでは、単に数を基準に選んでいく。このため、
・各記述子について、相関係数が閾値を超えているものをリスト化する
・リストの要素が多い順にforループを回して、各リストに含まれている記述子を「読み込まない記述子」リストに入れていく
・基準となっている記述子は、「読み込む記述子」リストに入れていく
・「読み込まない記述子」リストに含まれている記述子は、forループで順番が回ってきても、操作をスキップする（「読み込む記述子」リストに入れない）
という作業を行う。この操作によって、あまり効率的ではないが、「記述子B」のようなものを、ピックアップすることができるだろう。これを実現するコードは、以下のようになる。

#(i)相関係数を計算
desc_corr=desc.corr()

#(ii)相関係数が閾値（絶対値で0.95より大）を上回る場合は、星取表がTrueになるデータフレームの作成
desc_corr_bool = (((desc_corr>0.95)&(desc_corr<1.00) | (desc_corr<-0.95)&(desc_corr>-1.00)))

#(iii)各記述子がkey、上記の条件を満たした要素がvalueである辞書を作成する
desc_corr_dict = {col: desc.columns[desc_corr_bool[col]] for col in desc.columns}

#(iv)辞書の順番を並べ替えて、条件を満たす相関係数が多いものから順に並べる
sorted_col_corr = sorted(desc_corr_dict.items(), reverse=True, key=lambda x : len(x[1]))
sorted_col_corr = {tup[0]:tup[1] for tup in sorted_col_corr}

#(v)実際にforループを回して、記述子を振り分けていく
key_names = sorted_col_corr.keys()
skip_key = []
load_key = []

for key_name in sorted_col_corr.keys():
    if not key_name in skip_key:
        skip_key.extend(sorted_col_corr[key_name])
        load_key.append(key_name)

used_desc = desc[load_key]

各操作を解説していく。

#(i)相関係数を計算
desc_corr=desc.corr()
print(type(desc_corr))
#出力結果
#<class 'pandas.core.frame.DataFrame'>

相関係数は、(DataFrame).corr()で簡単に計算することができる。出力もデータフレーム型で、列、行には同じ名前が並び、各行・各列の交点には、行名・列名の示す記述子間の相関係数が入っている。

#(ii)相関係数が閾値を上回る場合は、星取表がTrueになるデータフレームの作成
desc_corr_bool = (((desc_corr>0.95)&(desc_corr<1.00) | (desc_corr<-0.95)&(desc_corr>-1.00)))

微妙に書き方がややこしいが、大したことはしていない。ポイントとして、
・データフレームを条件式の左辺に使うと、要素ごとに条件の判定をしてくれる
・出力として、元のデータフレームと同じサイズで、bool値を要素に持ったデータフレームを返す
ことを押さえれば良い。つまり、

desc_corr>0.95

では、データフレームdesc_corrの各要素が0.95より大きいか小さいかを判定し、各要素がTrueかFalseであるようなデータフレームを返す。続いて、

(desc_corr>0.95)&(desc_corr<1.00)

では、desc_corrと同サイズで、かたや0.95との大小、かたや1.00との大小を比較したデータフレームの要素同士を、&演算子で比較している。つまり、各要素同士を比べて、両方がTrueならTrue、片方でもFalseならFalseを要素とするようなデータフレームを返している。後半も同様の書式をしており、さらに得られた2つのデータフレームを|(or)演算子で比較している。なお、このような書き方をした場合は、演算子として'and'や'or'は使えず、それぞれ'&'や'|'となることには注意したい。

解析上の意味の話をすると、ここでは、「0.95 < 相関係数 < 1.00 または -1.00 < 相関係数 < -0.95」となるような相関係数をTrueとしている。この「0.95」という数字に深い意味があるわけではなく、完全に経験則なのだが、この閾値が大きすぎると記述子を減らす効率が悪くなるし、小さすぎると必要な記述子を落としてしまう危険が高まる。先に進もう。

(iii)各記述子がkey、上記の条件を満たした要素がvalueである辞書を作成する
desc_corr_dict = {col: desc.columns[desc_corr_bool[col]] for col in desc.columns}

#for文で書くなら、
#desc_corr_dict = {}
#for col in desc.columns:
#   mask = desc_corr_bool[col]
#   desc_corr_dict[col] = desc.columns[mask]

for文でのバージョンも書いたのは、説明の都合が良いから。まず、ある記述子に対して、その記述子と相関が大きい記述子のリストがある、という状況なので、辞書型を使うのが自然な発想になる（desc_corr_dict = {}）。続いて、desc_corr_bool[(記述子の名前)]には、その記述子と相関が大きければTrue、小さければFalseという具合にbool値が入っているので、これをmaskとして使うことができる(mask = desc_corr_bool[col])。最後に、desc.columnsが、記述子の一覧が並んだリストになるので、これにmaskを適用して、辞書に格納すればよい(desc_corr_dict[col] = desc.columns[mask])。これらの操作を内包表記で書くと、冒頭の一行になる。

#(iv)辞書の順番を並べ替えて、条件を満たす相関係数が多いものから順に並べる
sorted_col_corr = sorted(desc_corr_dict.items(), reverse=True, key=lambda x : len(x[1]))
sorted_col_corr = {tup[0]:tup[1] for tup in sorted_col_corr}

ここでは、作成した辞書を、valueのリストの要素数が大きい順に並べ替えている。ここでのポイントは、sorted関数の使い方（引数の説明）になる。、、、が、割とややこしい。
・引数として入力した辞書に「.items()」付けることで、返り値にkeyとvalueの両方を含めることができる
・reverse=True とすることで降順にする
・key=(関数)とすることで、並びかえの基準を作ることができる
を押さえておけば、ここは理解できると思う。より詳しい情報は、以下のサイトを参照してほしい。また、返り値はタプルを格納したリストになっているので、2行目で辞書型に書き直している。

次で最後の操作になる。

#(v)実際にforループを回して、記述子を振り分けていく
key_names = sorted_col_corr.keys()
skip_key = []
load_key = []

for key_name in sorted_col_corr.keys():
    if not key_name in skip_key:
        skip_key.extend(sorted_col_corr[key_name])
        load_key.append(key_name)

used_desc = desc[load_key]

まず、並び替えた辞書のkeyをforループの基準にする（key_names = sorted_col_corr.keys()）。続いて、読み込まない記述子を格納するリスト（skip_key）、および、読み込む記述子を格納するリスト（load_key）を作成する。これらを使って、forループを回している。ポイントは、「if not key_name in skip_key:」の行で、これがあることで、「互いに相関が大きい記述子のクラスター」から、「相関が大きい記述子の総数が最も多い記述子」だけを取り出すことができている。

実際には、最後のforループで、先述の「値が一定の記述子を削除する」も同時に回せばいいので、下記のようになる。

for key_name in sorted_col_corr.keys():
    if (not key_name in skip_key) & (max(desc[key_name] != min(desc[key_name]))):
        skip_key.extend(sorted_col_corr[key_name])
        load_key.append(key_name)

以上で、「値が一定である」「他の記述子との相関が強い」という観点から、明らかに役に立ちそうにない記述子を削除することができた。ヒートマップを確認すると、これら2つの条件に合致してしまう記述子が消せていることがわかる。ここまでで、記述子の数を、271から102まで減らすことができた。

Borutaを使って記述子を減らす

続いて、Borutaを用いて記述子を減らしていく。Borutaについては、以下のページに詳しい。

つまり、ランダムフォレストをベースとして、「『目的変数との間に相関がないはずの記述子』よりも目的変数を解析するための能力が低い記述子」は役に立たないと判断している。部分的にでも相関が見える記述子（重要度が0でない記述子）を落とすのはなんとなく気がひけるが、そこに意味を見出してしまうのは、人間の情報処理能力の高さゆえ、と思って納得することにする。木目が人の顔に見えるようなものだ。

Borutaの使い方は、上記サイト以上に説明できる気がしないので、ここではコードと簡単な説明にとどめる。

from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import train_test_split
from boruta import BorutaPy

train_desc, test_desc, train_prop, test_prop = train_test_split(used_desc, prop)

rfr = RandomForestRegressor(max_depth=7)
feat_selector = BorutaPy(rfr, n_estimators='auto', two_step=False, verbose=2, random_state=42)
feat_selector.fit(train_desc.values,train_prop.values)

selected = feat_selector.support_

desc_selected = used_desc[used_desc.columns[selected]]

これで、記述子の数を、32まで減らすことができた。かなり減ってきた。

ランダムフォレストの重要度を使って記述子を減らす

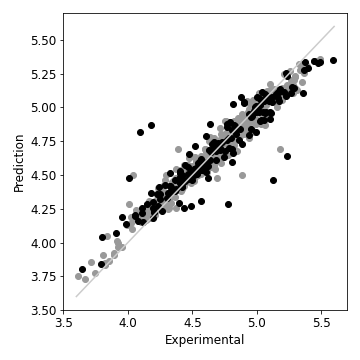
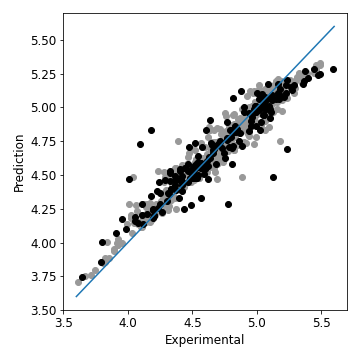
最後に、ランダムフォレストの重要度を使って記述子を減らしていく。とりあえず、現在ある記述子を全部使って、回帰を回してみると、以下のような結果が得られる。灰色のプロットは訓練データ、黒色のプロットがテストデータで、灰色の直線はexperimentalとpredictionが一致しているラインを表す。ここのところの説明は、そのうち別の記事で書くことにして、まあまあの予測結果、という印象である。

#ランダムフォレストで回帰する
desc_selected = used_desc[used_desc.columns[selected]]

train_desc, test_desc, train_prop, test_prop = train_test_split(desc_selected, prop, random_state=42)

rfr = RandomForestRegressor(max_depth=7)
rfr.fit(train_desc, train_prop)
pred = rfr.predict(test_desc)
pred_train = rfr.predict(train_desc)

fig = plt.figure(figsize=(5,5), tight_layout=True)
ax1 = fig.add_subplot(111)
plt.rcParams["font.size"] = 12

ax1.scatter(test_prop, pred, color='0', zorder=2)
ax1.scatter(train_prop, pred_train, color='0.6', zorder=1)

x = [3.6, 5.6]
ax1.plot(x,x, color='0.8')

ax1.set_xlabel('Experimental')
ax1.set_ylabel('Prediction')
fig.savefig('rfr_1.png')

さて、ここで得られた重要度をもとに、記述子の絞り込みをおこなっていく。と言っても、重要度の閾値を幾らかに設定して、それ以下を削除する、というやり方は取らない。「ランダムフォレストで回帰して、重要度の一番低かった記述子を削除する」という操作を繰り返し行う。また、記述子の削除による回帰の精度の低下はR2スコアで評価する（削除した記述子の数 vs. R2スコア のグラフを作成する）。
なんでこんなことをするかというと、ランダムフォレストは、先に述べた、多重共線性の影響を、モロにうける。例えば、相関係数が、互いに1であるような記述子が含まれていると、分岐において、どちらの記述子を使ってもいいので、重要度を仲良く分け合ってしまう。このような効果によって重要度が相対的に下がっている記述子が存在する可能性は、当然ある。この場合、片方の記述子が消えれば、もう片方の重要度は上がってくるはずだ。つまり、記述子の削減前後で、ランダムフォレストが元々持っているランダム性以上の、より本質的な影響によって、重要度が入れ替わる可能性があるわけだ。そこで、記述子を削除するたびごとに、重要度の一番低いものを削除する、ということを行う。

まずは、これからやりたい操作のパーツに相当する部分を作っていく。
最初に、一番大事な「記述子を重要度の順番に並べる」にあたる部分のコードが、以下の通りだ。まず、記述子の列名が使った記述子になるので、これを取得する（features = train_desc.columns）。続いて、回帰により得られた重要度を取得する（importances = rfr.feature_importances_）。これを昇順で並び替えた場合のインデックスの並び順を取得し（indices = np.argsort(importances)）、先に作成しておいたfeaturesから、必要な部分だけ取り出す(mask = features[indices[1:]])。argsortでは、昇順になっているので、先頭のインデックスを読み込まなければいい、という理屈で、indices[1:]となっている。最後に、used_descからmaskだけを取り出せば、無事、「一番重要度が低い記述子」を削除できたことになる。

features = train_desc.columns
importances = rfr.feature_importances_
indices = np.argsort(importances)
mask = features[indices[1:]]
masked_desc = used_desc[mask]

もう一つ、重要なパーツは、R2スコアを計算する部分だ。まあ、これは元からある機能を使うだけなので、以下のように計算すればよい。実際に機械学習を行う部分については、また別記事で書くので、ここではフーンと思っておいてもらえればいい。

pred = rfr.predict(test_desc)
r2 = r2_score(test_prop, pred)

これらのパーツを適宜並べ替えつつ、元の記述子の数-1回だけループを回す（記述子の数が0になってはいけないので）ことにすると、以下のようなコードになる。

#一番最初の回帰のR2スコアはr2_initialとしておいた
r2_scores = [r2_initial]
#削除した記述子の数を入れていくリスト
del_num = [0]

#ランダムフォレストの設定
rfr = RandomForestRegressor(max_depth=7)

#各ステップで、どのような記述子を使用したかも記録しておく
feature_set = [features]

for i in range(initial_features_num-1):
    mask = features[indices[1:]]
    masked_desc = used_desc[mask]

    train_desc, test_desc, train_prop, test_prop = train_test_split(masked_desc, prop, random_state=42)

    rfr.fit(train_desc, train_prop)

    pred = rfr.predict(test_desc)
    r2 = r2_score(test_prop, pred)

    r2_scores.append(r2)
    del_num.append(i+1)

    features = train_desc.columns
    feature_set.append(features)
    importances = rfr.feature_importances_
    indices = np.argsort(importances)

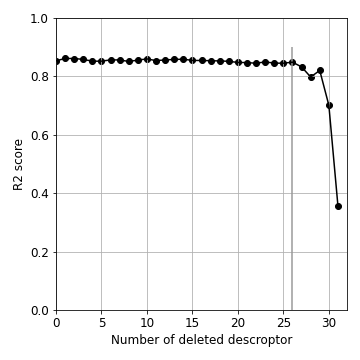
これによって得られた「削除した記述子の数 vs. R2スコア」のグラフは、以下の通りだ。記述子を削除した数が、26を超える（27以上削除する）と、急激にR2スコアが悪化することがわかる。どうやら、これ以上削ると、回帰に必要な情報が失われてしまうらしい。

fig = plt.figure(figsize=(5,5), tight_layout=True)
ax1 = fig.add_subplot(111)
plt.rcParams["font.size"] = 12

ax1.scatter(del_num, r2_scores, color='0')
ax1.plot(del_num, r2_scores, color='0')

ax1.set_xlim(0, 32)
ax1.set_ylim(0, 1)

#plt.hlines(y=0.8, xmin=0, xmax=31, color='0.6')
plt.vlines(x=26, ymin=0, ymax=0.9, color='0.6')

ax1.grid()

ax1.set_xlabel('Number of deleted descroptor')
ax1.set_ylabel('R2 score')
fig.savefig('del_num_vs_r2.png')

26個記述子を削除した段階で残っている記述子は、feasure_set[26]なので、以下のように取り出せる。

feature_set[26]
#出力結果
#Index(['max:covalent_radius_pyykko_triple', 'ave:evaporation_heat',
#       'var:vdw_radius_uff', 'var:heat_capacity_molar',
#       'sum:electron_affinity', 'temperature'],

記述子を6個まで減らすことができた。もう十分だろうと思う。ちなみに、これらの記述子を使った回帰の結果は、以下の通りである。最初と比べるとよくはないが、そんなに悪くもなく、まあこんなもんかな、というような結果だろう。

まとめ

今回の記事では、いくつかの手法により、記述子の数を減らす、という操作をおこなった。ここで重要なのは、最後の6個に絞るところまでほとんど材料化学の知識は使っていない、という点にある。もしも、ここで残された記述子のうち、解釈不能なものが残っていれば、それが「データ科学によって、材料化学にもたらされた知見」と言ってもいいと思う。

とはいえ、現在、目に見えて得られている記述子をそのまま信じてはいけない。理由は2つある。
・相関係数が大きい記述子に入れ替えても、回帰の結果に変化はない
・ランダムフォレストの重要度 = 材料化学としての重要性 ではない（かもしれない）
1つめは、例えば、最終結果に「原子番号」という情報が残ったとして、これが物性に影響を与えているわけではないことは明白である。例えば、原子番号と相関の強い記述子（原子量）が重要である、という考えた方がいい。こうした議論をするためには、記述子を一個一個入れ替えてみて、回帰の結果が極端に変化しないことを確認しながら、「~という理屈で物性に影響を与えています」という仮説を立ててみるべきだ。こういったことを考えながら解析を行えるところに、材料化学者が、自分の手で機械学習を行う価値があると思う。
2つ目の方は、より重要かもしれない。要するに、ランダムフォレスト（というか決定木）の分岐点として登場する回数と、材料化学としての重要性が、ダイレクトにつながっているのか、というと、正直「？」である。もちろん、「これらの重要性は一致するよ」という立場に立って議論することは、積極的におこなっていいと思うし、実際やっているのだが、この立場（というか仮説）に立っている、ということは明示しておいた方がいいだろう、と思っている。

長々と書いてしまったが、以上にする。今回の記事で、なんとなくランダムフォレストを使って回帰したが、次回の記事では、使用するアルゴリズムの選定について、もう少し真面目に書きたい。