はじめに
この記事で書くこと
この記事は、材料系かつ実験系の研究者が機械学習を始めるための第一歩になりそうなことを書く。「マテリアルズインフォマティクス」という言葉が人口に膾炙し、「未知の材料の探索」だの「数百年に一度の発見」だの喧伝されているが、そういうことはしない。「条件探索に4回実験を回さなければならないところを、3回に減らす」とか、「必要特性を満たす落としどころ組成のあたりづけをする」とか、そういう、もっと意識の低いことをしたい。実際のところ、そのくらいの使い勝手の「道具」の方が、現場的には役に立つことが多いと思っているし、個人的な期待が大きい。
この記事で使うもの
・Starry Data 2
東京大学の桂ゆかり先生( https://twitter.com/nezdenmama )のStarry Dataプロジェクトからデータを持ってくる。アクセスしてみればわかるが、ものすごいデータ量である。内容の信頼性も高いので、これからデータ科学的に材料化学データを扱いたい人にはもってこいのデータベースである。
https://sites.google.com/site/yukarisearch/starrydata
・Xenonpy
統計数理研究所吉田研究室で開発されている。このページに辿り着いている時点で、Xenonpyがなんなのか把握していると思うので、説明は省く。
簡単にデータを扱ってみる
データを読み込んで眺める
Starry Data 2を触ったことがない人は、ひとまず上記サイトにアクセスして、いろいろ遊んでみてほしい。それだけでもかなり面白い。一しきり堪能したら、この記事で扱うデータを持ってくる。Visualizationタブをクリックし、左のカラムから、Electrical ConductivityとComposition、Temperatureにチェックを入れて、データをダウンロードする。ダウンロード時には、csvを指定し、Encodingはutf-8、Indentation codeとDelimeterは環境に合わせる。下図参照。

そしたら、pandasでデータを読み込んで、内容を見てみる。データ量が多いので、Excelで読み込むのはお勧めしない。
import pandas as pd
# x,yには適当な数字を入れる
df0 = pd.read_csv('data.csv')
df0[x:y]
あまりコーディング的に正当な使い方ではないことを承知で書くが、df0[x:y]のxとyの数字を適当に変えて読み込んでみると、どうやらTemperatureとcompositionは必ずデータが入っていて、Electrical conductionにはNaNが結構含まれていることがわかる。ここでは、Electrical conductionに対して解析がしたいので、ここがNaNになっているデータは、もったいないけど捨ててしまう(.dropna(how='any'))ことにする。ついでに、.reset_index()で、行番号を振り直しておく。
df1 = df0.dropna(how='any').reset_index()
df1.head()
# 出力結果
# index Electrical conductivity Temperature composition
# 0 77 65795.817779 500 Pb1Te1.01Na0.02
# 1 78 47428.264423 550 Pb1Te1.01Na0.02
# 2 79 21161.382780 700 Pb1Te1.01Na0.02
# 3 81 26019.711633 650 Pb1Te1.01Na0.02
# 4 83 93048.908125 450 Pb1Te1.01Na0.02
これで、全ての行にElectrical conductivityのデータが含まれることになった。さて、これを元に解析を進めるわけだが、そもそも「解析」とは、物理量 vs. x という関係をプロットした時に、意味のある'x'を探すことだ。現状、手持ちのデータには、xにできるものがTemperatureしかないし、Electrical conductivity vs. Temperatureは、自明な結果しか与えない。そこで、Xenonpyの力を借りて、xに相当するものの候補、つまり記述子を計算してもらう。
Xenonpyで記述子を計算する
Xenonpyでは、いくつかの記述子の計算機を提供しているが、ここでは組成式を元に記述子を計算してもらうことにする。ちなみに、構造(pymatgenのStructureデータ)を元に記述子を計算してもらうこともできる。(動径分布関数に直すらしい。力技感がすごい。)Xenonpyの記述子計算機(xenonpy.descriptor.Compositions)は、公式チュートリアルが以下にあるが、引数として辞書型のデータを必要とする。つまり、M2O3みたいな組成の化合式だと、{'M':2, 'O':3}のような形式のデータを準備しなければならない。
元データに含まれている組成式を、この辞書型に成形するために、pymatgenを利用する。
from pymatgen.core import Composition
Composition('Fe2O3').as_dict()
# 出力結果
# defaultdict(float, {'Fe': 2.0, 'O': 3.0})
このように、簡単に組成式を辞書型に直してくれる。df1に新しく辞書型に直した組成のデータ列を追加する。
df1['comp_dict'] = [Composition(comp).as_dict() for comp in df1['composition']]
df1.head()
# 出力結果
# index Electrical conductivity Temperature composition comp_dict
# 0 77 65795.817779 500 Pb1Te1.01Na0.02 {'Pb': 1.0, 'Te': 1.01, 'Na': 0.02}
# 1 78 47428.264423 550 Pb1Te1.01Na0.02 {'Pb': 1.0, 'Te': 1.01, 'Na': 0.02}
# 2 79 21161.382780 700 Pb1Te1.01Na0.02 {'Pb': 1.0, 'Te': 1.01, 'Na': 0.02}
# 3 81 26019.711633 650 Pb1Te1.01Na0.02 {'Pb': 1.0, 'Te': 1.01, 'Na': 0.02}
# 4 83 93048.908125 450 Pb1Te1.01Na0.02 {'Pb': 1.0, 'Te': 1.01, 'Na': 0.02}
それでは、Xenonpyに記述子を計算してもらおう。
from xenonpy.descriptor import Compositions
cal = Compositions()
descriptor = cal.transform(df1['comp_dict'])
# 記述子に温度も追加しておく
descriptor['temperature'] = df1['Temperature']
descriptor.head()
出力結果は長いので省略するが、290個の記述子を計算してくれた。290個というと、とても多い気がするのだが、原子番号や原子質量など、材料研究をしている人間なら、まあ概ね思いつくような記述子(要するに特性)が58個と、これらの平均、分散、合計、最大、最小、という統計量からなるもので、眺めてみると、意外とそんなものか、という感想になるだろう。
ヒートマップを描く
続いて、これを元に、ヒートマップを作成する。ここでいうヒートマップとは、詳細な依存関係を捨てて、代わりに一覧性を持たせたデータ表記の仕方である。まずは、どんなものか、見てもらう。表示自体は簡単にできる。
from xenonpy.visualization import DescriptorHeatmap
# データを並べ替える
prop = df1['Electrical conductivity']
sorted_prop = prop.sort_values()
sorted_desc = descriptor.loc[sorted_prop.index]
# ヒートマップを描く
heatmap = DescriptorHeatmap(
save=dict(fname='heatmap_density', dpi=200, bbox_inches='tight'), # save figure to file
figsize=(20, 10)) #この行は図のサイズを決める。環境に合わせて変えるのが吉。
heatmap.fit(sorted_desc)
heatmap.draw(sorted_prop)
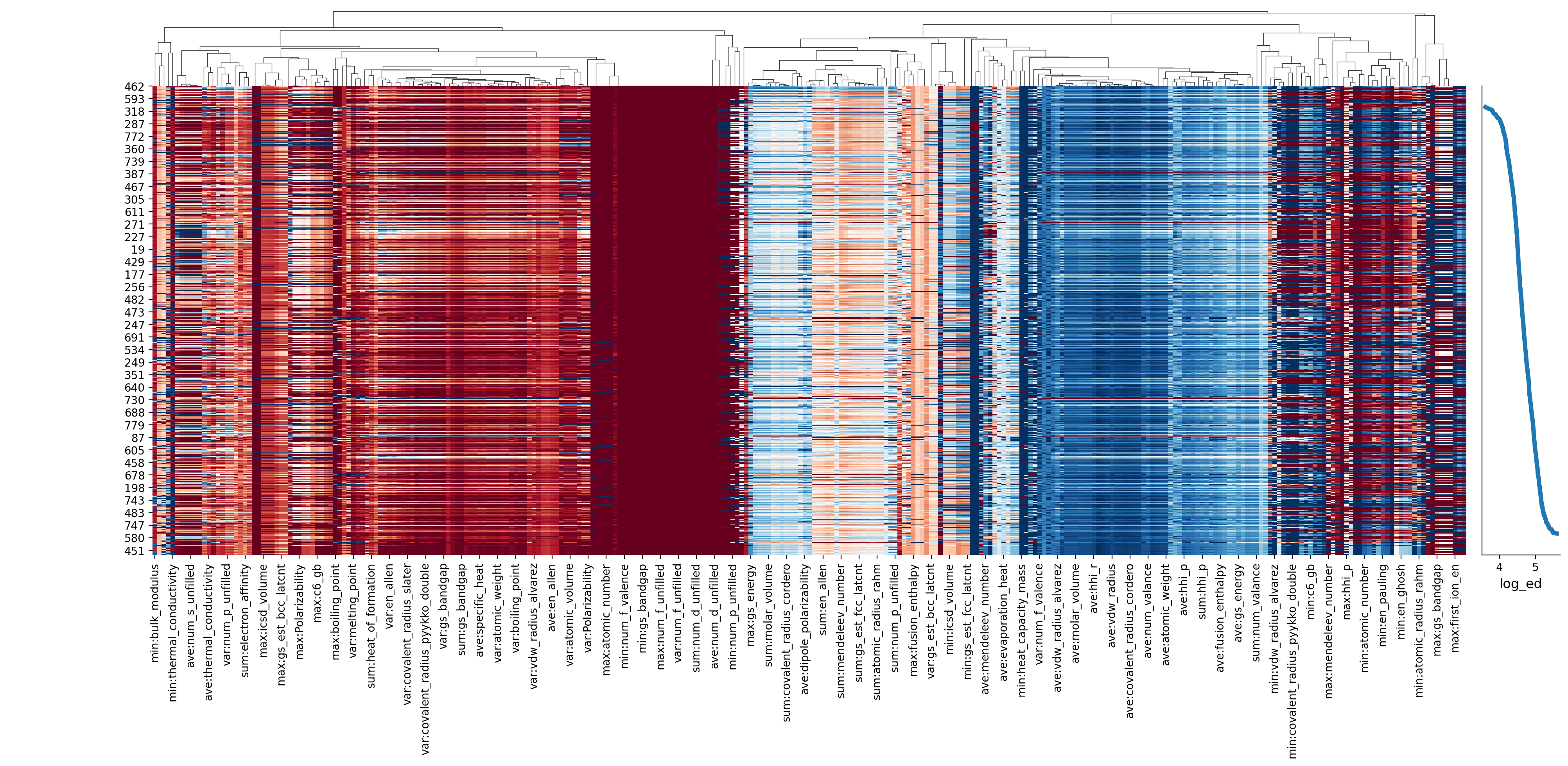
ここでは、コードと合わせて真面目にヒートマップの概略を解説することにする。まず、以下の部分では、データを並べ替えている。propに解析の目的である物性値を入れ、数値の低い方から順に並べ替えている(.sorte_values)。
# データを並べ替える
prop = df1['Electrical conductivity']
sorted_prop = prop.sort_values()
結果として得られたsorted_propには、元データに含まれるElectric conductivityの値が、低い順に並んでいることになる。
print(sorted_prop)
# 出力結果
# 462 4115.345885
# 465 4365.523382
# 129 4664.383079
# 461 5217.657197
# 126 5507.213412
# ...
# 517 298998.410305
# 525 308766.182703
# 459 309175.637672
# 439 311384.021606
# 513 389213.356957
左の数字は、indexである。.sort_valueでは、indexがふり直されない。この仕組みを利用して、以下のコードで、記述子の入ったデータフレームを並べ替える。
sorted_desc = descriptor.loc[sorted_prop.index]
# 右辺は、descriptor.loc[[462, 465, 129, 461, 126...517, 525, 459, 439,513]]と同じ意味.
これで準備ができたので、以下のコードでヒートマップを描く。'save='の行で画像を保存しているので、画像を保存したくない時は、この行をコメントアウトすればよい。また、'figsize='で画像サイズを指定している。この数字は、環境に応じて適当に変えると吉。
heatmap = DescriptorHeatmap(
save=dict(fname='heatmap_density', dpi=200, bbox_inches='tight'),
figsize=(20, 10))
heatmap.fit(sorted_desc)
heatmap.draw(sorted_prop)
ヒートマップの見方
さて、ここでこのヒートマップだが、検索しても、これが何を表しているのかわからず、初心者には「???」となってしまう(パターンが多いと思っている)。しかも、Xenonpyの使い方を見ていると、割と最初の方に出てくるので、僕はここで一回挫折した。そこで、以下に簡単に解説を付した。下図には、簡単な解説を記載している。ここでは、ヒートマップを見やすくするために、記述子を減らして表示している。
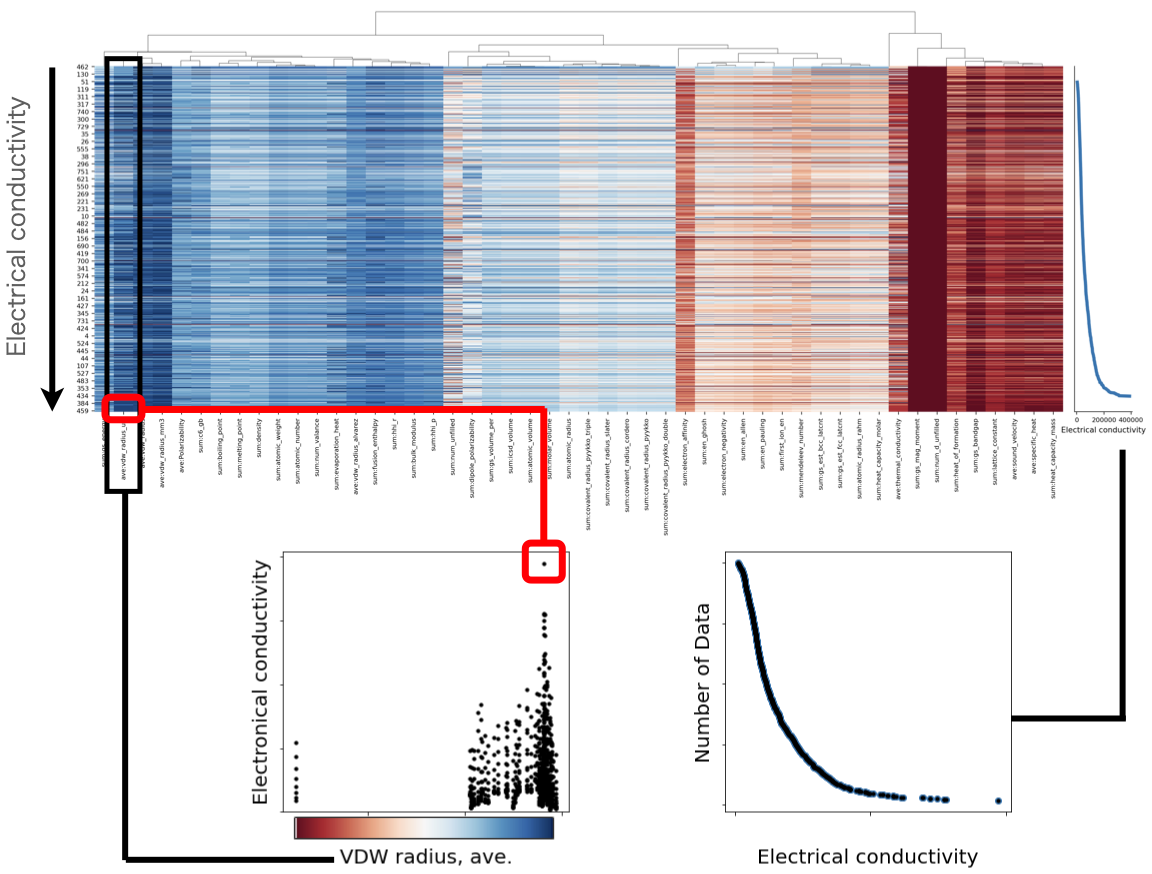
先に書いたことを改めて書くが、ここでいうヒートマップは、詳細な依存関係を捨てて、代わりに一覧性を持たせたデータ表記の仕方である。記述子の数を減らしたので、ヒートマップでは、横に向かって、短尺状に区切られた空間に分かれていることがわかると思う。この1つ1つが、各記述子に対応している。上図では、ここから1つ例(Van der Waals(vdw)半径の平均)を取り出している(左下グラフ)。
グラフを見ればわかるように、データはvdw半径の、比較的大きいところに集中している。カラーバーも合わせて載せてあるので、データが青い領域に集中しているのを見てもらいたい。さらに1点に注目(赤で示した)すると、Electrical conductivityが最も大きいデータ点(ヒートマップ上で一番下)のところは、vdw半径の一番大きいところに当たるので、ヒートマップ状では深い青色になっている。この例でわかるように、相対的な大小の感覚は掴めるが、具体的な数値は読み取れない。冒頭に述べた「詳細な依存関係を捨て」というのはこれを指す。一方、すでに見たように、多くの記述子を並べて表示できており、自分が準備した記述子が、どのように目的の物理量に影響を与えているか、一覧できるようになっている。グラフを大量に並べても、このように一覧するのは難しい。
また、右下に示した図は、ヒートマップの右側に示されているグラフを拡大したものである。縦軸は、下の方が値が大きくなっている。物性量の、どの数値範囲に、どの程度データ点数があるかがわかるようになっている。理屈の上では、縦軸を横軸の変数で微分すれば、ヒストグラムになる。今回使ったデータセットでは、Electrical conductivityの小さい領域に、多くのデータがあるのがわかる。Electrical conductivityのように、数桁の範囲にデータが散らばっていると、このような分布になるのは自然なことに思える。
蛇足
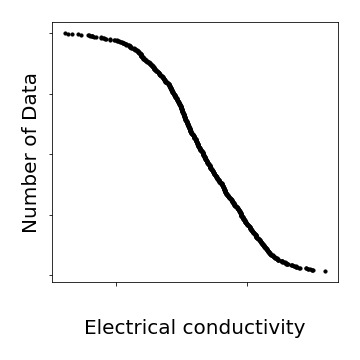
普通に考えると、データの値範囲について、データはできるだけ一様に散らばっているのが望ましい。これは現実には難しいが、Electrical conductivityの場合は、以下の通り、logをとればいける。Electrical conductivityであれば、logを取るのも自然である。なんでもlogをとればいいわけではないが、今回は割とうまくいった。
まとめ
今回は、
・Starry Data 2からデータを持ってきて、
・記述子を計算し、
・ヒートマップを描く
ことをおこなった。以上。