Python ニュートン法を実装する

ニュートン法とは

1変数では初期値 $x_0$ を設定し、以下の数列によって関数 $f$ の近似解を求める方法。

x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)} 

多変数では初期値 $\boldsymbol{x_0} \in \mathbb{R}^n$ を設定し 、関数 $f: \mathbb{R}^n \rightarrow \mathbb{R}^n$ の近似解を求める方法。

$$\boldsymbol{x_{n + 1}} = \boldsymbol{x_n} - H^{-1} f(\boldsymbol{x_n})$$

ここで $H$ はヘッセ行列。

1変数

こちらに置きました。

import sympy as sp
import numpy as np
import matplotlib.pyplot as plt

def newton_method(f, x, init_value, num):
    df = sp.diff(f, x)
    next_value = 0
    for i in range(num):
        next_value = init_value - f.subs(x, init_value) / df.subs(x, init_value)
        init_value = next_value
    return next_value
    
if __name__ == '__main__':
    x = sp.Symbol('x')
    # ここで関数を設定する
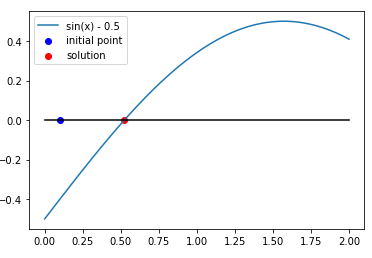
    f = sp.sin(x) - 0.5
    # ここで初期値を設定する
    init_value = 0.1
    # ここで繰り返し回数を設定する
    num = 10
    solution = newton_method(f, x, init_value, num)
    print(solution)

例 1

$${\rm sin}(x) - 0.5 = 0$$

初期値

0.5

出力

0.523598775598299

計算機での $\pi / 6$ の計算結果

0.52359877559829887307710723054658381403

誤差

1.2692289276945341618597101189910806429 E-16

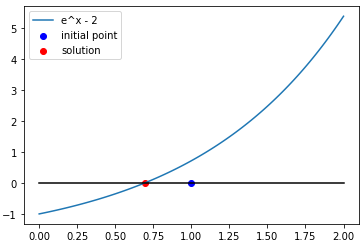
例 2

$$e^x - 2 = 0$$

初期値

1.0

出力

0.693147180559945

計算機での $e^x - 2 = 0$ の計算結果

0.69314718055994530941723212145817656807

誤差

3.0941723212145817656806814692747176370 E-16

多変数

import sympy as sp
import numpy as np

def newton_method(f, variables, init_value, num):
    for i in range(num):
        hesse = get_hesse(f, variables, init_value)
        subs_vector = np.array(
            [[f[i].subs(init_value)] for i in range(len(f))],
            dtype=float
        )
        init_vector = np.array(
            [[v] for v in list(init_value.values())],
            dtype=float
        )
        
        next_value = init_vector - np.linalg.inv(hesse) @ subs_vector
        init_value = {key: next_value[n][0] for n, key in enumerate(init_value)}
    return init_value

def get_hesse(f, variables, init_value):
    hesse = []
    for i in range(len(variables)):
        l = []
        row = []
        l.append(variables[i])
        for j in range(len(variables)):
            if len(l) == 1:
                l.append(variables[j])
            else:
                l[1] = variables[j]
            row.append(
                sp.diff(f[i], *l).subs(
                    init_value
                )
            )
        hesse.append(row)
    return np.array(hesse, dtype=float)

if __name__ == '__main__':
    x = sp.Symbol('x')
    y = sp.Symbol('y')
    z = sp.Symbol('z')
    variables = [x, y, z]
    # ここで関数を設定する
    f = [x ** 2 - 2, (x ** 2) * (y ** 2) - 4, x * z ** 2 - 1]
    # ここで初期値を設定する
    init_value = {x: 1, y: 2, z: 0.3}
    # ここで繰り返し回数を設定する
    solution = newton_method(f, variables, init_value, 50)
    print(solution)

例 1

\left\{
\begin{array}{l}
x^2 - 2 = 0 \\
x^2 y^2 - 4 = 0 \\
x z ^2 - 1 = 0
\end{array}
\right.

初期値

{x: 1, y: 2, z: 0.3}

出力

{x: 1.414213562373095, y: 1.4142135623730954, z: 0.8408964152537146}

解（初期値に近い値）

$$x = \sqrt{2}, y = \sqrt{2}, z = \sqrt{1/\sqrt{2}}$$

上記の解の計算機での計算結果

x = 1.4142135623730950488016887242096980786
y = 1.4142135623730950488016887242096980786
z = 0.84089641525371454303112547623321489504

誤差

x: 4.8801688724209698078596369014359646933 E-17
y: 3.5119831127579030192140409244737913280 E-16
z: 5.6968874523766785104960243772098740359 E-17

参考記事