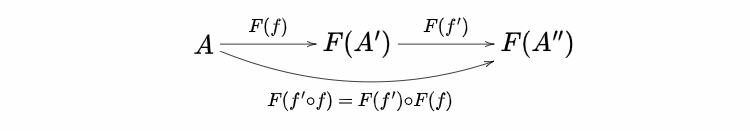初めに
本記事は体系的に圏論を勉強するには不十分です。仕事そっちのけで絶賛圏論勉強中エンジニアが細々と書いているだけです。他に良記事はたくさんあります。そっと戻るボタンを押してください。
前回、圏の定義に関する記事を書きました。
圏の定義について振り返ります。圏とは
- 対象
- 対象間の射と呼ばれる矢印
- 射の合成と呼ばれる射
- 恒等射
からなり、射が結合法則と単位法則を満たすものをいいました。
今回は関手について書きます。関手は圏と圏の対応に関する概念です。今回も『哲学者のための圏論入門』を参考に関手の背景について紹介します。また『ベーシック圏論』も参考にしています。
関手とは何か
関手の導入部分を『哲学者のための圏論入門』から引用します。
ここまではずっと、ひとつの圏 $\textbf{C}$ を固定してその中でいろいろと新しい対象を定義してきたわけですが、今度は一段視野を拡げて、圏と圏の間の関係性、さらには圏と圏の間の関係性の間の関係性を記述する言葉を用意するわけです。それが、関手(functor)であり自然変換(natural transformation)です。
圏と圏の間の関係性を記述するものが関手です。『ベーシック圏論』からも関手について引用します。
圏論の一つの教訓は、新しい数学的対象に出くわすたび、それらの間の理にかなった「射」の概念が存在するかをつねに問うてみるべきだということである。これを圏そのものについて適用してみよう。その答えは肯定的で、圏の間の射は関手と呼ばれている。
それらの間の理にかなった「射」の概念が存在するかをつねに問うてみる、と述べられている通り、圏論では矢印が主役です。
関手の定義
定義(関手)
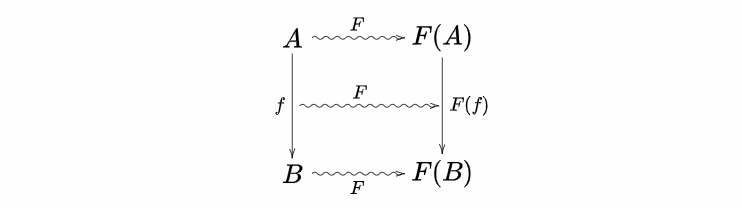
$\mathscr{A},\ \mathscr{B}$ を圏とします。関手 $F:\mathscr{A}\to \mathscr{B}$ とは、次のような対応を備えています。
- $\mathscr{A}$ の対象 $A$ を $\mathscr{B}$ の対象 $F(A)$ にうつす対応
- $\mathscr{A}$ の対象 $A,\ A'$ に対して、射 $f:A\to B$ を $\mathscr{B}$ の射 $F(f):F(A)\to F(B)$ にうつす対応
この $F$ は次を満たします。
-
$\mathscr{A}$ の対象 $A,\ A',\ A''$ と射 $f:A\to A',\ f':A'\to A''$ に対して $$F(f'\circ f) = F(f')\circ F(f)$$
-
$\mathscr{A}$ の対象 $A$ に対して $F(1_A) = 1_F(A)$
関手の例
関手の例を挙げてみたいと思います。
例 1
$k\in \mathbb{N}$ を 1 つ固定します。任意の $i\in \mathbb{N}$ に対して、$A_i := \lbrace i\rbrace,\ B_i := \lbrace i^k\rbrace$ と定めます。$A_i,\ A_j$ の間の射を $f_{ij}:A_i\to A_j$、$B_i,\ B_j$ の間の射を $g_{ij}:B_i\to B_j$ とします。$\mathscr{A}$ を $A_i$ を対象とする圏、$\mathscr{B}$ を $B_i$ を対象とする圏とします。$F:\mathscr{A}\to \mathscr{B}$ を
$$F(A_i):=B_i,\ F(f_{ij}):=g_{ij}$$ と定めることで $F$ は関手となります。このことを確認します。
$$F(f_{jk}\circ f_{ij}) = F(f_{ik}) = g_{ik} = g_{jk}\circ g_{ik} = F(f_{jk})\circ F(f_{ij})$$ となります。また
$$F(1_{A_i}) = F(f_{ii}) = g_{ii} = 1_{B_i} = 1_{F(A_i)}$$ となります。したがって $F:\mathscr{A}\to \mathscr{B}$ は関手です。
例 2
例 1 では対象が集合であり、射が写像になっているので、internal な視点に立っている感じがします。そこで次のように external な視点に立ってみます。
任意の $i\in \mathbb{N}$ に対して、$\mathscr{A}$ を $A_i$ を対象とする圏、$\mathscr{B}$ を $B_i$ を対象とする圏とします。$A_i,\ A_j$ の間の射を $f_{ij}:A_i\to A_j$、$B_i,\ B_j$ の間の射を $g_{ij}:B_i\to B_j$ とします。$F:\mathscr{A}\to \mathscr{B}$ を
$$F(A_i):=B_i,\ F(f_{ij}):=g_{ij}$$ と定めることで $F$ は関手となります。このことの確認は例1と同様です。
この例では、$A_i, B_i$ は集合である必要はないし、$f_{ij}$ は写像である必要はありません。
例 3
例 2 において、添え字だけに着目します。すなわち、$\mathscr{A}$ の対象 $A_i$ を $i$、$\mathscr{B}$ の対象 $B_i$ を $i$、射を $i\to j$ と考えます。すると、$\mathscr{A}$ と $\mathscr{B}$ はそれぞれ $\mathbb{N}$ になり、$F$ は $\mathbb{N}$ から $\mathbb{N}$ への関手となります。さらに
$$F(i) = i,\ F(i\to j) = i\to j$$ となります。自明な関手になりました。『圏と関手入門』によると、これを恒等関手と呼ぶそうです。