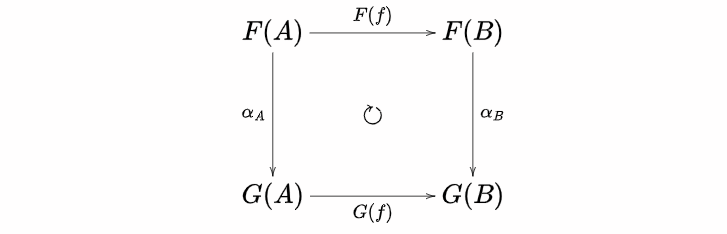
自然変換の定義
定義（自然変換）
$\mathscr{A},\ \mathscr{B}$ を圏、$F,\ G$ をそれぞれ $\mathscr{A}$ から $\mathscr{B}$ への関手とします。$\alpha:F\to G$ が自然変換であるとは、射の族 $(\alpha_A:F(A)\to G(A))_{A\in \mathscr{A}}$ が、$\mathscr{A}$ の任意の射 $f:A\to B$ に対して
$$\alpha_B\circ F(f) = G(f)\circ \alpha_A$$ を満たすことをいいます。
自然変換の例
『ベーシック圏論』から例を引用します。
$\mathbf{CRing}$ を対象が可換環で射が環準同型という圏、$\mathbf{Mon}$ を対象がモノイドで射がモノイド準同型からなる圏とします（モノイド準同型とはモノイドに定義された演算を保ち、かつ単位元を単位元にうつす写像のこと）。まず $\mathbf{CRing}$ から $\mathbf{Mon}$ への関手を 2 つ定めます。$n\in \mathbb{N}$ を 1 つ固定しておきます。
まず、$F:\mathbf{CRing}\to \mathbf{Mon}$ を定めます。$A\in \mathbf{CRing}$ とします。$A$ 成分の $n\times n$ 行列 $(a_{i,\ j})$ 全体がなすモノイドを $M_n(A)$ とします。$M_n(A)$ の演算は行列の積です。もちろん $M_n(A)\in \mathbf{Mon}$ です。$F(A):=M_n(A)$ と定めます。
次に $F$ による射の行き先を定めます。$A,\ B\in \mathbf{CRing}$ に対して環準同型写像 $f:A\to B$ は、モノイド準同型写像
$$F(f):M_n(A)\to M_n(B),\ (a_{i,\ j})\to (f(a_{i,\ j}))$$ を誘導します。これで $F(f)$ も定まりました。$f,\ f'$ を $\mathbf{CRing}$ の関手とすると、$F(f'\circ f) = F(f')\circ F(f)$ が成り立ちます。また $F(1_{\mathbf{CRing}}) = 1_{\mathbf{Mon}}$ も成り立ちます。以上により、$F$ は関手です。
次にもう一つの関手 $G:\mathbf{CRing}\to \mathbf{Mon}$ を定めます。こちらは簡単です。$A\in \mathbf{CRing}$ は乗法とその単位元によりモノイド $U(A)$ とみることができます。$G(A):=U(A)$ と定めます。集合としては変わりませんが、環に定義された加法を取り去ります。$G$ による射の対応も同じです。環準同型 $f:A\to B$ に対して、$G(f)$ には $f$ から加法の構造を保つことを取り去ったモノイド準同型を対応させます。これで 関手 $G$ も定まりました。
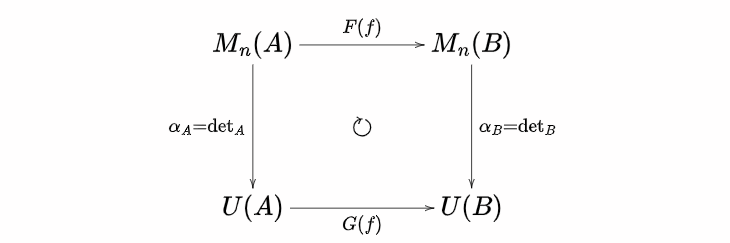
ここからは自然変換 $F\to G$ を定めます。各 $A\in \mathbf{CRing}$ に対して
$$\alpha_A:F(A) \to G(A),\ (a_{i,\ j})\to \text{det}((a_{i,\ j}))$$ と定義します。$\alpha_A$ はモノイド準同型であるため、$\alpha_A$ は $\mathbf{Mon}$ の射になります。
$\alpha_B\circ F(f) = G(f)\circ \alpha_A$ を確認します。$X:=(a_{i,\ j})$ とおきます。
左辺の合成 $G(f)\circ \alpha_A$ を計算していき、右辺に等しくなることを確認します。
$$G(f)(\alpha_A(X))= G(f)(\text{det}_A(X)) = f(\text{det}_A(X))$$ となります。さらに、行列式と環準同型と $F(f)$ の定義から
$$f(\text{det}_A(X)) = \text{det}_B(F(f)(X)) = \alpha_B(F(f)(X))$$ となります。これで右辺の合成と等しくなりました。以上により $\alpha$ が自然変換であることが確認できました。