$\newcommand{\argmax}{\mathop{\rm arg~max}\limits}$$\newcommand{\argmin}{\mathop{\rm arg~min}\limits}$
この記事は古川研究室 Workout_calendar 18日目の記事です.
本記事は古川研究室の学生が学習の一環として書いたものです.内容が曖昧であったり表現が多少異なったりする場合があります.
はじめに
学内での勉強会にて,kNNの説明を担当する機会がありました.その際は,単純にアルゴリズムや特徴の説明にとどまっていましたので,Qiita投稿週間のこの機会に実装も行い発信しようと考え,今回記事にまとめることにしました.
コードの部分については,冗長であったり,非効率的な処理が多々あると思います.
暖かい目で見守っていただければ幸いです.
kNNとは
k最近傍法(k-Nearest Neighbor: kNN)とは,教師あり学習の一手法であり,クラス未知のサンプルのクラスラベルを近傍サンプル $k$ 個による多数決で決めようというシンプルな手法です.$k$ は自由に決めることができるハイパーパラメータです.
以下にkNNによるクラス判別のイメージを示します.

予め,赤,青,黄の三つのクラスに分類されたサンプルが与えられているとします.
今,クラスの分からない新たなサンプルが観測されました.図では白色になってるサンプルです.
このクラスが未知のサンプルのクラスを,kNNによって決定します.
ハイパーパラメータ $k=4$ とした場合のクラス判別の例を以下に示します.
$k=4$ としたので,クラス未知のサンプルの最近傍サンプルを$4$つ選びます.以下のようになります.

クラスが未知のサンプルの$4$つの最近傍サンプルの内訳は,赤:$0$,青:$3$,黄:$1$となりました.多数決の結果,新たなサンプルのクラスは青に決定しました.
近傍の定義
上記のクラスタリングの例では,特に何の説明もせずに最近傍サンプルを決めていましたが,実は「ユークリッド距離」というピタゴラスの定理によって与えられる二点間の距離が小さい順に最近傍サンプルを決めていました.
kNNにおいては,「ユークリッド距離」を使うことが一般的とされていますが,明示しているのであれば,その他の距離を用いても問題ありません.
識別のリジェクト
$k$個の最近傍サンプルの内訳がすべて同じ数になり,多数決でクラスを決定できないときはどうなるでしょうか.これについては,識別を放棄(リジェクト)する,もしくは完全にランダムに決定するといったような解決策がとられます.
kNNの識別ルール
kNNの識別ルールを定式化すると以下のようになります.
$k_i \quad (i=1,...,m)$ はクラス未知の観測データの最近傍サンプル $k$ 個のうち,クラス $i$ に所属するサンプルの個数です.
$$
識別クラス =
\begin{cases}
\argmax_{1\leq i\leq m} k_i \quad & if \quad f({k_i}_{i=1}^m) = 1 \
reject \quad & otherwise \
\end{cases}
$$
$$
※k = \sum_{i=1}^m k_i
$$
ここで $f$ は引数として集合を受け取り,集合の要素のうち最大値がいくつあるのか,その個数を出力する関数です.
例として,$f$ が集合 $X=\{1,3,5,6,10,7,10\}$ を引数にとると,要素のうち最大値は $10$ であり,その個数は $2$ であるため,以下のようになります.
$$
\begin{align}
f(X) &= f(\{1,3,5,6,10,7,10\}) \\ &= 2
\end{align}
$$
kNNの弱点,気を付けるべきこと
計算量
アルゴリズムが非常にシンプルなので,実装も容易なkNNですが弱点もあります.
その弱点とは,観測データ数が増えるほど計算コストが大きくなってしまうことです.
これは,クラス未知のサンプルの $k$ 個の最近傍サンプルを発見するために,データ空間にあるすべてのサンプルとの距離を計算しなければいけないことに起因します.全探索必須なクラス判別手法であるため,実装の際は処理が重くなりがちです.
計算量は,サンプル数が $n$ 個で各サンプルが $d$ 個の要素を持つ( $d$ 次元)場合,以下のようになります.
$$
\mbox{kNNの計算量} : O(nd)
$$
kの選び方
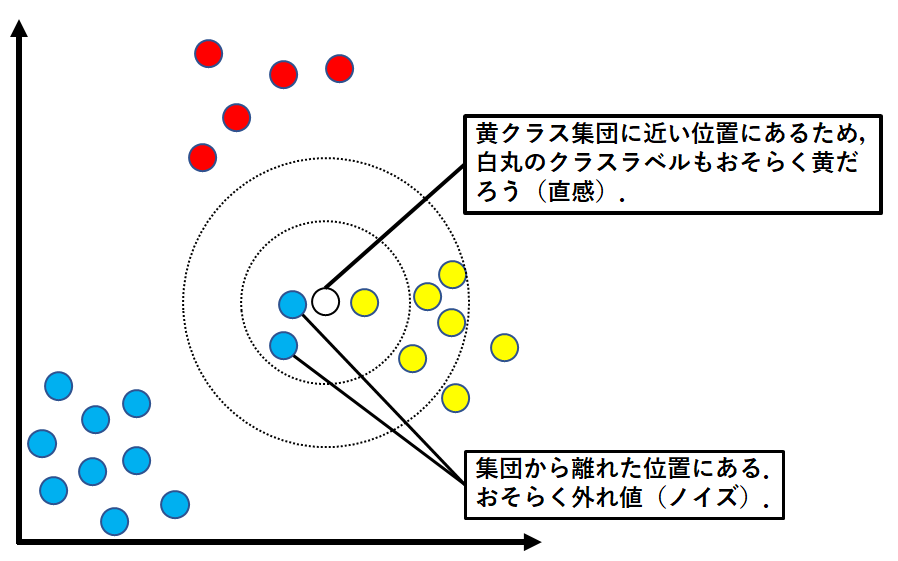
kNNを用いる際は $k$ の選び方についても慎重にならなければなりません.
観測データである白丸の近傍には青と黄のサンプルがあります.
サンプルの分布をみると,観測データの所属クラスは黄クラスかなと,多くの人が考えると思います.
しかし,$k=3$としてkNNを適用してみると,観測データの所属クラスは青クラスと判別されます.
これは,青クラスの集団から外れ値(ノイズ)が発生し,偶然,観測データがノイズの近くに位置していることに起因します.
$k=5$とすると,黄クラスと判別され,私たちの直感と同じ判別結果が得られます.
上記のことより,$k$ の値が小さいとノイズの影響を受けることがあり,クラス判別を正しく行えない可能性があることがわかります.
また,与えられたサンプルの数に偏りがある場合もハイパーパラメータ $k$ の値を慎重に選ばなければ,誤分類を引き起こすことがあります.これについては,後ほど出てくる実装パートにて体感して頂けると思います.
kNNの実装
実際にkNNを実装しました.見ていきましょう.
必要なライブラリをインポート
import numpy as np
import matplotlib.pyplot as plt
データセットの作成
赤,青,緑の3つのクラスのデータをつくる. クラスラベルは赤,青,緑の順に,1, 2, 3とします.
# 毎回同じ乱数が生成されるようにseedを固定しておきます.
# 再現性を担保するためです.
np.random.seed(seed=1)
x = list(np.random.randn(150))
y = list(np.random.randn(150))
C1x = []
C2x = []
C3x = []
C1y = []
C2y = []
C3y = []
index_list = []
for i,data in enumerate(y):
if x[i] >= 0:
if data <= -(x[i])/2: C3y.append(data), C3x.append(x[i]), index_list.append(i)
else:
if data <= 2*x[i]: C3y.append(data), C3x.append(x[i]), index_list.append(i)
index_list = np.sort(index_list)[::-1]
for i in index_list:
x.pop(i)
y.pop(i)
for i,data in enumerate(x):
if data > 0: C1x.append(data), C1y.append(y[i])
else: C2x.append(data), C2y.append(y[i])
dataset1 = [[i,j,'1'] for i,j in zip(C1x,C1y)]
dataset2 = [[i,j,'2'] for i,j in zip(C2x,C2y)]
dataset3 = [[i,j,'3'] for i,j in zip(C3x,C3y)]
dataset = np.vstack((dataset1,dataset2,dataset3))
fig = plt.figure(figsize=(12, 8))
plt.scatter(C1x,C1y,color='red',s=10)
plt.scatter(C2x,C2y,color='blue',s=10)
plt.scatter(C3x,C3y,color='green',s=10)
plt.show()
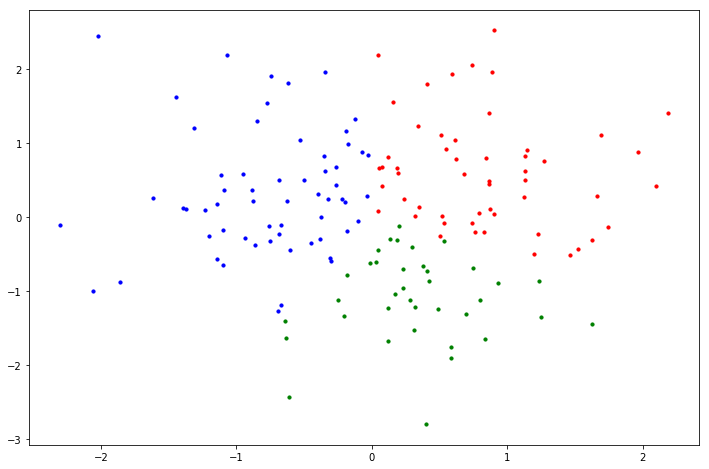
上記のコードを実行した結果がこちら.いい感じに赤,青,緑に分かれたサンプルデータがゲットできました.
クラスが未知のデータを観測
クラスが未知のデータを観測した体で,観測データの特徴量を乱数で決める.
(正規分布に従う乱数を使ってますが,その他でもかまいません.)
np.random.seed(4)
unknown_data = np.random.randn(2)
print(unknown_data)
fig = plt.figure(figsize=(12, 8))
plt.scatter(C1x,C1y,color='red',s=10)
plt.scatter(C2x,C2y,color='blue',s=10)
plt.scatter(C3x,C3y,color='green',s=10)
plt.scatter(unknown_data[0],unknown_data[1],color='black',s=100)
plt.show()
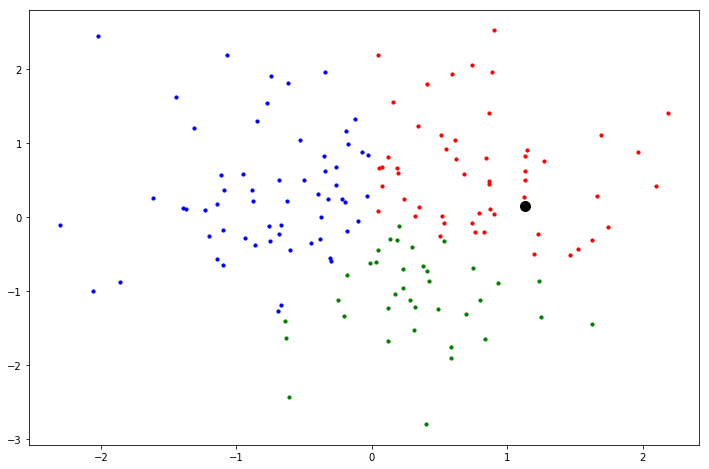
実行すると以下のような図を出力します.黒い点が観測データです.まだクラスが分からないので黒色にしています.
kNNによるクラス判別
$k$ の値と,クラス未知の観測データの特徴量を受け取ったのち,クラス判別を行い,そのままプロットしてくれる関数を書きました.以下の通りです.
def kNN(k,u):
#全サンプルと観測データ間のユークリッド距離を計算する.
#その際,距離を計算したサンプルのラベルも記憶しておく
dist_list = []
label_list = []
for i,j in enumerate(dataset):
dist_list.append([np.sqrt((float(j[0])-u[0])**2+(float(j[1])-u[1])**2),j[2]])
#print(dist_list[i])
#距離が小さい順に並べ替える
dist_list.sort()
#最近傍サンプルk個でクラス判別のための多数決を行う
class_label = [0,0,0]
for i in range(k):
if dist_list[i][1] == '1': class_label[0] += 1
elif dist_list[i][1] == '2': class_label[1] += 1
elif dist_list[i][1] == '3': class_label[2] += 1
print("最近傍サンプル",k,"個の内訳 : [赤(1),青(2),緑(3)] =",class_label)
print()
print("kNNによる判別の結果,観測データのクラスラベルは", class_label.index(max(class_label))+1, "です.")
if class_label.index(max(class_label))+1 == 1: color = 'red'
elif class_label.index(max(class_label))+1 == 2: color = 'blue'
elif class_label.index(max(class_label))+1 == 3: color = 'green'
fig = plt.figure(figsize=(12, 8))
plt.scatter(C1x,C1y,color='red',s=10)
plt.scatter(C2x,C2y,color='blue',s=10)
plt.scatter(C3x,C3y,color='green',s=10)
plt.scatter(unknown_data[0],unknown_data[1],color=color,s=100)
plt.show()
それでは,上の関数に任意のkの値と観測したデータを与えてkNNによるクラス判別を体感してみましょう!
まずは $k=10$ とした場合です,どうぞ!
kNN(10,unknown_data)
出力がこちらです!
最近傍サンプル 10 個の内訳 : [赤(1),青(2),緑(3)] = [8, 0, 2]
kNNによる判別の結果,観測データのクラスラベルは 1 です.
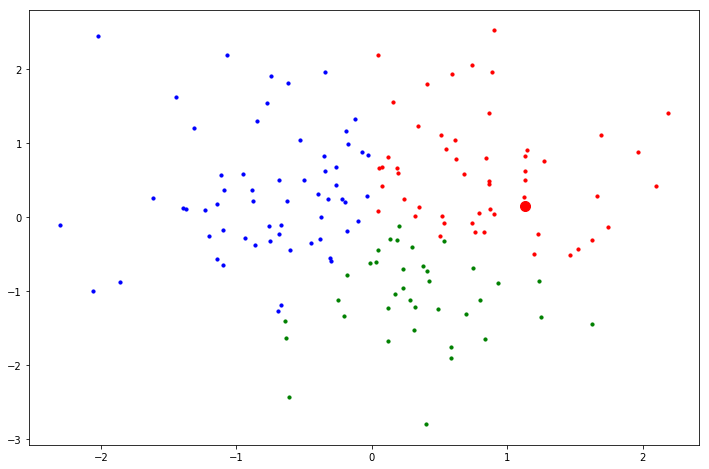
kNNを適用した結果,観測データのクラスは赤(ラベル1)となりました.
まあ,そりゃそうだろって感じですよね.
では,ここで $k=150$,つまり全サンプルを用いてkNNを適用してみましょう.何が起こるでしょうか?
kNN(10,unknown_data)
出力がこちらです!
最近傍サンプル 150 個の内訳 : [赤(1),青(2),緑(3)] = [44, 69, 37]
kNNによる判別の結果,観測データのクラスラベルは 2 です.
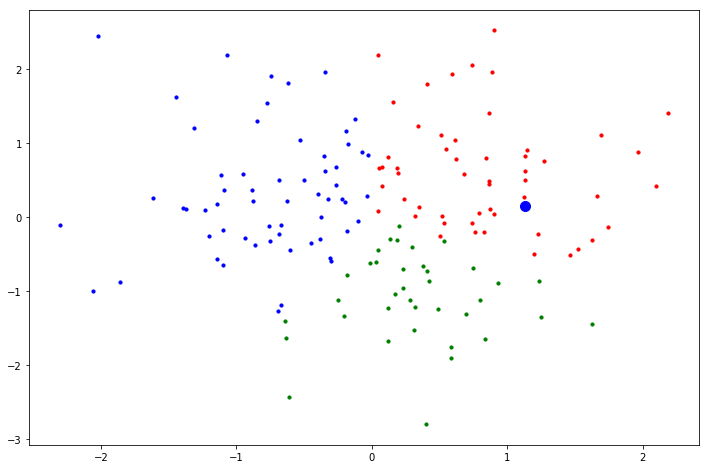
kNNを$k=150$として適用した結果,観測データのクラスは青色(ラベル2)になってしまいました.$k=150$としたことで,私たちの直感とは異なる結果になってしまいました.
なぜでしょうか?
先ほどの出力を再掲します.
最近傍サンプル 150 個の内訳 : [赤(1),青(2),緑(3)] = [44, 69, 37]
kNNによる判別の結果,観測データのクラスラベルは 2 です.
最近傍サンプル $150$ 個の内訳というのは,$150=$ 全サンプル数 なので,全サンプル数の内訳ということになります.
全サンプルのうち,青クラスが過半数を占めているために,先ほどのような結果になってしまったのです.
kNNを適用する場合はハイパーパラメータ$k$を慎重に選ばなければ,誤判別を発生してしまうということを体感することができました.
おわりに
本記事ではkNNについて説明を行い,実際に実装し,その挙動を確認しました.シンプルなアルゴリズムのkNNですが,その分類の誤り率について研究者らの間で議論が繰り広げられたり,面白い歴史を持つ手法の一つです.次回の記事では,その面白い歴史に少しだけ触れる内容を取り上げる予定です.読んでいただければ嬉しいです.
参考資料
[1] はじめてのパターン認識.平井有三
[2] わかりやすいパターン認識.石井健一郎,上田修功,前田英作,村瀬洋
[3] はじめてのパターン認識 第5章 k最近傍法(k_nn法) - SlideShare