運の良し悪しを可視化してみる

これは 非公式 Infocom Advent Calendar 2023 11日目の記事です。

「ここに1枚100円で引けるくじがあります。99本に1本の割合で当たりが入っていて、当たりの賞金は10000円です。何枚買いますか？」
…って聞かれたら、もちろん有り金全部突っ込んで無限に買い続けますよね？

世の中にはそんなくじ引きが存在しています。もちろん合法で。
例えばこちらのバーサスリヴァイズというスロットマシンがそうです。打ち手のミスがなければ、一番最低の設定でも機械割102%（平均的にはメダル100枚分プレイすると102枚の払い出しを受けられる仕様）となっています。ただし、くじ引きには運要素があり、一日や一週間の単位では収束しません。毎回のくじ引きは独立した試行です。

そんなわけで、理論値100%オーバーのスロットマシンを暇を見つけてプレイしてみた累積結果を可視化してみます。

対象マシンの概要

今回打ち込んだマシンには4段階の設定があり、最低設定のスペックはおよそ以下の通りです。

• 完全技術介入時の機械割：102%
• 理論上の当たり確率：1 / 156

最低スペックでもこの数値ですから、お店には基本的に最低設定しか置かれていないと思って間違いありません。でもいいんです。
また、私は完全にミスなく打ち切ることはできないので、実際の機械割はこのスペックからは少し下がって 101.4〜101.5% 程度になります。でも十分です。

理論上は、くじを156回引く（156ゲーム分プレイする）と1回当たることになります。ただ、2回連続で当たることもあれば、1000回引いても当たらないこともあります。あくまで、長い目で見たときに、平均で156回に1回当たるということになります。

データ

日々の記録はこんな感じのフォーマットで蓄積しています。当たりが出ると、一定量のメダルが獲得できます。差枚数はメダルの払い出し枚数から投入数を引いたもので、プラスであればこちらの勝ち、マイナスは負けを意味します。

日付	くじ引き回数	当たり回数	差枚数
2023/7/23	5351	31	-782
2023/7/30	1205	10	+301
2023/9/24	7704	53	+1102
...	...	...	...

現在までの累計値としては、総くじ引き回数が275117回、総当たり回数が1688回です。
平均すると約163回に一度の割合で当たっていることになるので、理論値の1/156に対して引き負けていますが、この差はいかほどのものでしょうか…。

グラフを描画してみる

横軸にくじ引きの回数、縦軸に差枚数を取ってグラフにしてみます。
全くミスせずに打ち切ったときの期待値（102%）、実力を加味した期待値（101.4%）と合わせて、実績値を描画します。

# 完璧に打った場合の機械割
PERFECT_PAYOUT = 1.02
# 技術力を考慮した現実的な機械割
EXPECTED_PAYOUT = 1.014

# データ読み込み
import pandas as pd

df = pd.read_csv("data.csv")
n_plays = df["くじ引き回数"]
n_wins = df["差枚数"]

# グラフ描画
import matplotlib.pyplot as plt

plt.figure(dpi=256, figsize=(12, 8))
# 完全攻略時の期待差枚数（3枚掛け）
plt.plot(n_plays, n_plays * 3 * (PERFECT_PAYOUT - 1), color="red", linestyle="dashed", label=f"ノーミス時の期待値（{PERFECT_PAYOUT * 100}%）")
# 実力を考慮した期待差枚数（3枚掛け）
plt.plot(n_plays, n_plays * 3 * (EXPECTED_PAYOUT - 1), color="orange", label=f"実力ベースの期待値（{EXPECTED_PAYOUT * 100}%）")
# 実際の成績
plt.plot(n_plays, n_wins, color="blue", label="実績")
# プラマイゼロの線
plt.plot(n_plays, n_plays*0, color="gray", linestyle="dotted")
# ラベルと軸の調整
plt.title("累計差枚数")
plt.ylabel("累計差枚数")
plt.xlabel("累計回転数")
plt.xlim(0, plays[-1])
plt.legend()
plt.show()

...なんということでしょう。
オレンジが私の期待値、青が実績値ですが、グラフにしてみると恐ろしく乖離しています。その差10000枚以上。金額にするとMacbook Airの15インチが買えそうです。平均156回に1回当たるくじを約28万回引き続けていることになりますが、全く収束する様子が見えません。
三つくらいの区間に分けて見ると、序盤の5万回までの凹み方がえげつない。中盤の5万回目〜20万回目あたりはおよそ期待値通りに推移していますが、終盤の20万回目以降は横ばいになってしまっています。

このくじ引き運については、とにかく試行回数を増やすしかありませんが、ちょっと運が悪すぎるような気がします。どのくらい悪いのでしょうか。

確率分布に当てはめる

運を定量的に表現するために、確率分布に当てはめてみます。
「ある期間に平均λ回起こる低確率な現象が、ある期間にX回起きる確率の分布」であるポアソン分布を使用します。

y = scipy.stats.poisson.pmf(x, mu)

pmf（Probability mass function）は、離散値xの入力に対しての起こりやすさを返します。muにはその現象が起こる期待値λを指定します。
平均156回に1回当たるはずのくじを275117回引いた時に期待できる当たり回数の確率分布に対して、今回の試行結果である1688回の当たりを重ねて描画すると以下のようになります。離散型の確率分布は通常棒グラフで表現しますが、目がチカチカするので線グラフにしました。

from scipy.stats import poisson
import matplotlib.pyplot as plt
import numpy as np

# くじ引き回数
n_plays = 275117

# 当たり回数
n_bonus = 1688

# 確率分母
rate = 156

# 理論上の当たり期待回数
mu = n_plays / rate

# 描画するレンジ（平均値の前後150回）
xrange = 150
xs = np.arange(int(mu - xrange), int(mu + xrange), 2)

# 描画するレンジにおける確率分布
ys = [poisson.pmf(x, mu) for x in xs]

# 今回の試行結果に対する確率
y = poisson.pmf(n_bonus, mu)

# 確率分布に実績値を重ねて描画
plt.figure(dpi=150)
plt.title(f"{n_plays}回くじ引き時の当たり回数の確率分布（1/{rate}）")
plt.plot(xs, ys, color="blue")
plt.bar([n_bonus], [y], color="red", label=f"当たり回数＝{bonus_counts}回")
plt.xlabel(f"当たり回数")
plt.xlim(xs[0], xs[len(xs)-1])
plt.legend()
plt.show()

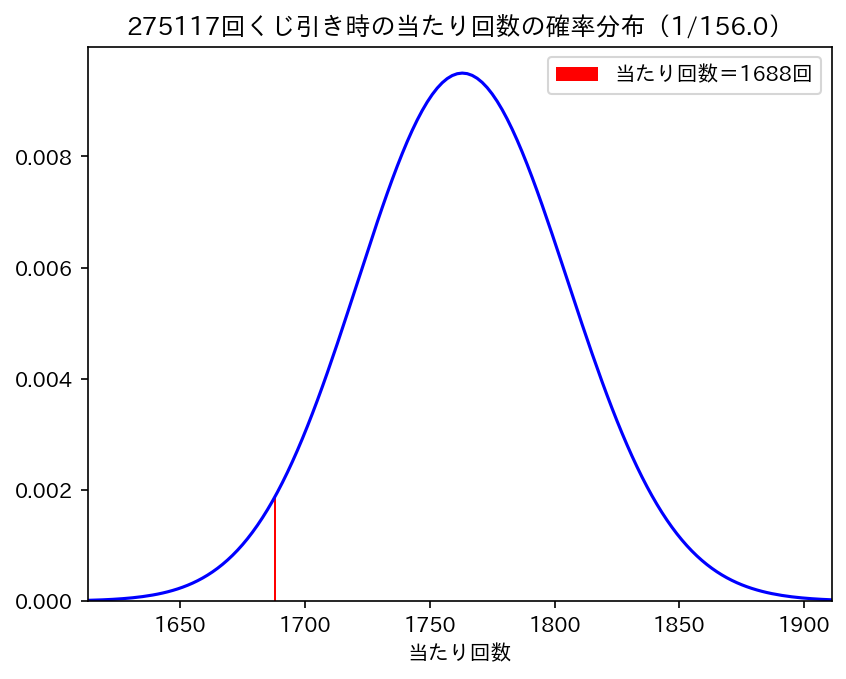
うむ…。
理論上の平均回数は 275117/156 = 1763回なので、1688回は悪い部類なのは間違いありませんが、かなり薄いところを引いている感じがありますね…。

累積確率で見てみます。

y = scipy.stats.poisson.cdf(x, mu)

cdf（Cumulative distribution function）は、期待値muの分布において事象が起こる回数がx以下となる割合を返します。

# 描画するレンジにおける累積分布
ys = [poisson.cdf(x, mu) for x in xs]

# 今回の試行結果に対する確率
y = poisson.cdf(n_bonus, mu)

# 累積率分布に実績値を重ねて描画
plt.figure(dpi=150)
plt.title(f"{n_plays}回くじ引き時の当たり回数の累積分布（1/{rate}）")
plt.plot([xs[0], n_bonus], [y, y], color="red", linestyle="dashed")
plt.text(xs[0]+2, y+0.02, f"{y*100:.1f}%")
plt.plot(xs, ys, color="blue")
plt.bar([bonus_counts], [y], color="red", label=f"当たり回数＝{bonus_counts}回")
plt.xlabel(f"当たり回数")
plt.ylabel("累積確率")
plt.xlim(xs[0], xs[len(xs)-1])
plt.legend()
plt.show()

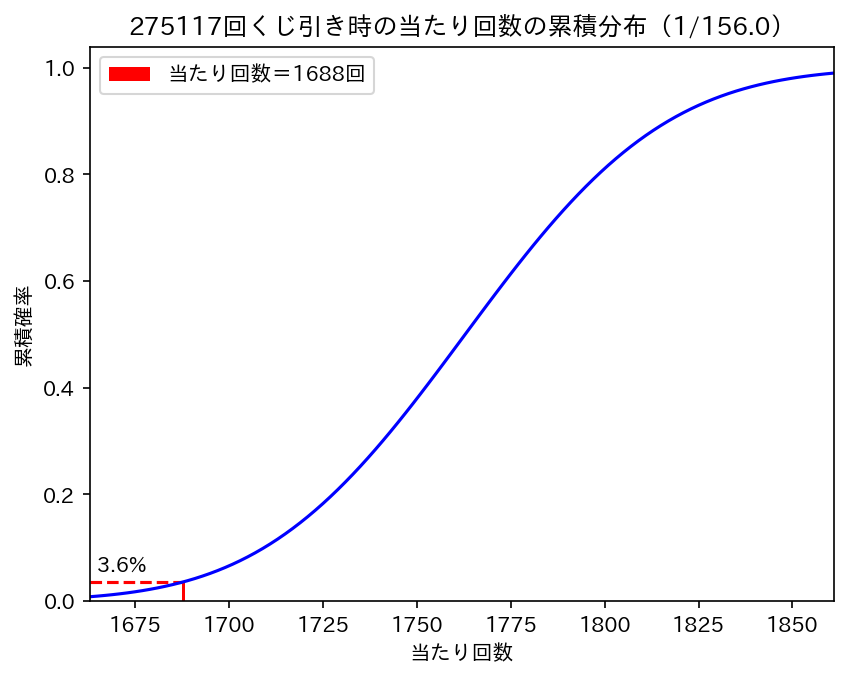
1/156のくじを275117回引いて、1688回の当たりが出るのは下位3.6%となりました。
30人くらい集めて一番運の悪い人を選んだら自分だった、と。
果たして収束する日は来るのか…。

（撤去される日までつづく）