標準正規分布の確率密度関数の積分を検証する
$\displaystyle\int_{-\infty}^{\infty} \frac{1}{\sqrt{(2\pi)}}e^{-x^2/2} dx = 1$
を検証します。
Rで左辺を計算してみる
積分範囲は($-\infty$から$\infty$と取るのは不可能なので、代わりに)$-100$から$+100$として計算してみます。
# 被積分関数の定義
s <- function(x){
exp(-x^2/2)/sqrt(2*pi)
}
# 積分の実行
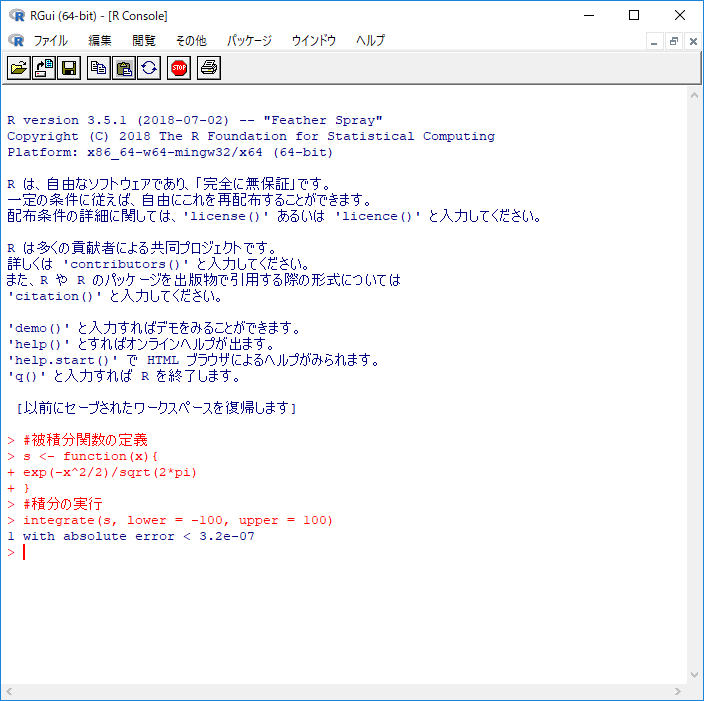
integrate(s, lower = -100, upper = 100)
出力結果は
1 with absolute error < 3.2e-07
となります。積分結果は$1$であり、計算誤差は$3.2\times 10^{-7}$であるという結果です。
積分範囲は適当にカットオフしましたが、検算の意味では十分でしょう。$|x|>100$の領域でこの確率密度はほぼ0になるということです。
下記は実行時のスクショ。
手計算で検証する
まず次の定積分$I$を用意します。
$$I=\int_{-\infty}^\infty e^{-x^2}dx$$
$I$を自乗し、$x=r\cos\theta,y=r\sin\theta$と置換します。$dxdy=rdrd\theta$より
$$I^2 = \int_{-\infty}^\infty dx\int_{-\infty}^\infty dy e^{-(x^2+y^2)}=\int_0^\infty dr re^{-r^2}\int_0^{2\pi}d\theta=\pi$$
となり$I=\sqrt{\pi}$が示せます。$I$の積分で、$x\to x/\sqrt{2}$と置換すれば、題記の積分が示せます。
より詳しくは「ガウス積分」で検索してみましょう。