この記事は 量子コンピュータ Advent Calendar 2017 第18日目の記事です。
最近、量子コンピューターが流行っています。僕自身もそうなのですが、「なにかすごいらしい。でもなにができるのかわからない」とモヤモヤされている方も多いと思います。そこで、今回はいわゆるゲート方式(回路方式)の量子コンピュータのシミュレータを作成しながら、量子コンピュータの基礎の基礎を押さえていこうと思います。
なお、作成したコードはGistで公開しているので、興味のある方はいじってみてください。
対象読者
- 量子力学にあまり詳しくないが、量子コンピュータに興味のある方
- 簡単な行列計算(行列の掛け算)のできる方
量子力学とシュレディンガーの猫
量子コンピュータの話のまえに、まずはシュレディンガーの猫を題材に量子力学について説明します。
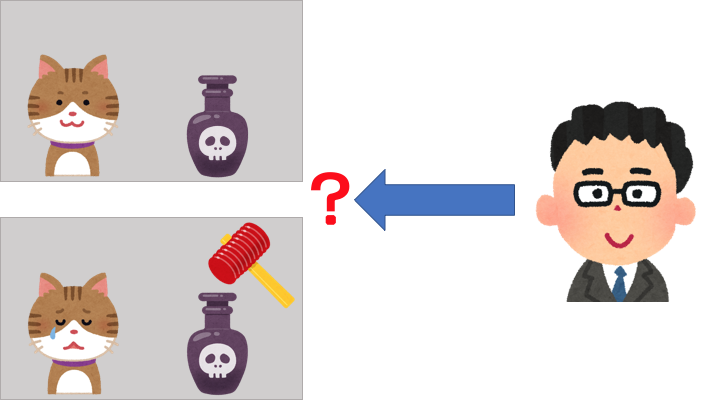
シュレディンガーの猫は、最も有名な思考実験の一つなので、ご存じの方が多いかと思います。この思考実験では、まず、中を見ることのできない箱の中に、猫と毒と放射性物質と放射線の検出器を入れ、放射線が検出されたら毒の瓶が割れるようにしておきます。そして、しばらく放置したあとで人間が覗きにいきます。
毒の瓶が割れると猫は死んでしまいますが、検出器が放射線を検出できるかどうかは確率の問題なので、確実に死んでしまうわけではありません。
普通に考えると、猫は毒の瓶が割られるまでは生きていて、割られてしまってからは死んでしまっています。一方、量子力学的には人間が中を覗くまでは生きている状態と死んでしまっている状態が重ね合わされた状態となっており、人間が覗いた時点で生きているかどうかが確定します。
シュレディンガーの猫は量子力学のパラドックスではありますが、量子力学の以下の性質を象徴しているように思えます。
- 量子力学では、複数の状態を重ね合わせた状態が存在する
- 観測すると、重ね合わせた状態から1つの状態が選ばれる
量子コンピュータと量子ビット
さて、量子力学では複数の状態を重ね合わせた状態が存在することがわかりました。量子コンピュータでは、この性質をつかって高速な演算を実現します。
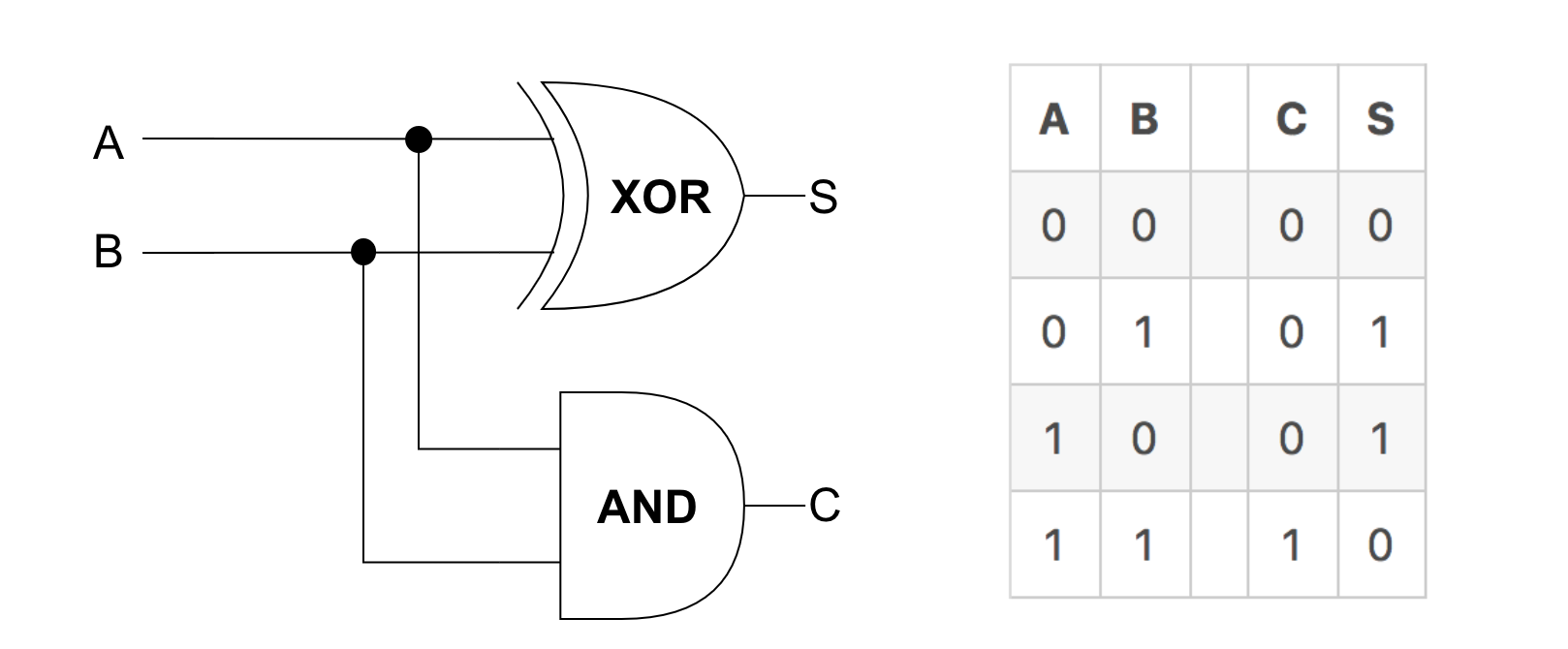
普通の(古典的な)コンピュータでは、0か1の値をとるビットを操作して演算を実行します。技術の授業で下図のような回路を見たことがあるかもしれません。これはビット同士の足し算をする回路です。
AやBがにそれぞれ0か1が入力されると、ANDやXORといった操作がされて、最終的に足し算した結果がCとSに出力されます。
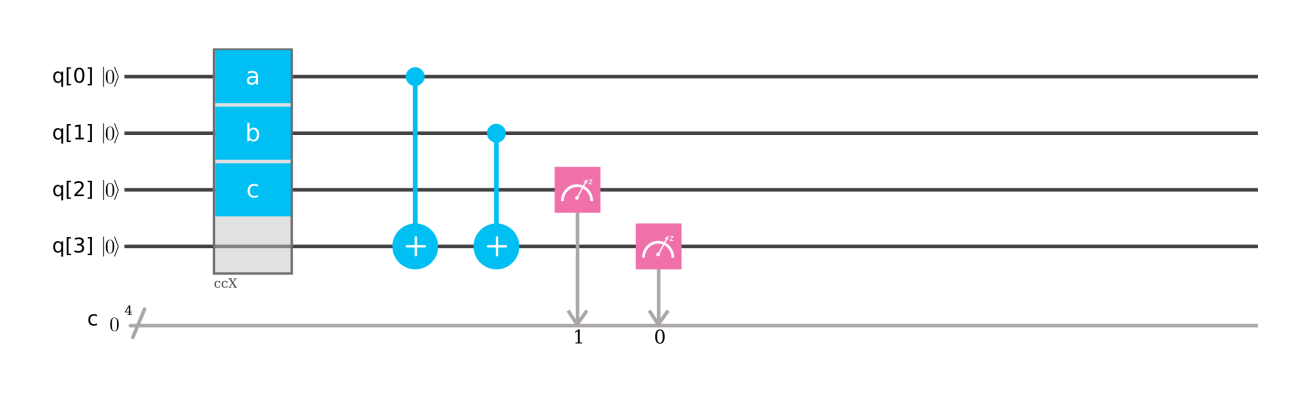
量子コンピュータでは、ビットの代わりに量子ビットと呼ばれるものにたいして操作を行います。足し算は以下の様になります。(IBM Q Experienceの実行結果)
上図の左端の q[n] が量子ビットをあらわしています($\left|0\right>$は古典的なビットの0に相当)。続くccXと書かれている部分がAND、2つの$\oplus$の部分がXORに対応しています。最後のメトロノームのような部分は、量子ビットを観測して(古典的な)ビットに代入することをあらわしています。
2つの回路図を見比べてみると、古典的なコンピュータと量子コンピュータの作りは非常に似ていることがわかります。ただし、大きな違いが2つあります。
- 各種の変換器の入力として重ね合わせの状態を使うことができる。
- 結果を利用するには、最後に観測しなければならない。
それぞれ前述の量子力学の性質と対応しています。量子ビットは古典的なビットと違い、 $\left|0\right>$ や $\left|1\right>$ に加えて、以下のような重ね合わせの状態をとることが出来ます。
$$\alpha\left|0\right> + \beta\left|1\right>$$
ここで $\alpha$ と $\beta$ は $|\alpha|^2 + |\beta|^2 = 1$ を満たすような複素数です。この重ね合わせの状態を観測すると、$|\alpha|^2$ の確率で $\left|0\right>$、$|\beta|^2$ の確率で $\left|1\right>$ となります。
量子コンピュータでは、この重ね合わせの状態を入力とすることで、高速に並列処理を行うことが出来ます。例えば、q[0]、q[1]ともに $\frac{1}{\sqrt{2}}\left|0\right> + \frac{1}{\sqrt{2}}\left|1\right>$ という状態を入力すると、
$$\frac{1}{\sqrt{2}}\left(\left|0\right> + \left|1\right>\right)\otimes\frac{1}{\sqrt{2}}\left(\left|0\right> + \left|1\right>\right)=\frac{1}{2}\left|0\right>\otimes\left|0\right> + \frac{1}{2}\left|0\right>\otimes\left|1\right> + \frac{1}{2}\left|1\right>\otimes\left|0\right> + \frac{1}{2}\left|1\right>\otimes\left|1\right>$$
となります。ここで、例えば $\left|0\right>\otimes\left|1\right>$ はq[0]が $\left|0\right>$ で、q[1]が $\left|1\right>$ である状態を表しており、簡単のため$\left|01\right>$ と書くこともあります。右辺をみると、q[0]とq[1]の4つの可能な組み合わせが全て重ね合わされていることがわかります。つまり、これを入力とすれば、たった1度で全ての状態について計算できることになります。
今回の例ではq[0]とq[1]の2量子ビットだったので、$2^2=4$つの状態でした。同様に$n$量子ビットの場合は$2^n$個の状態に対して同時に計算することができると期待されます。これが量子コンピュータが高速といわれる所以です。
ところが、これには問題があります。量子コンピュータの計算結果を利用するには、必ず観測をしなければなりません。そして、観測をしてしまうと、重ね合わせの状態がとけ、どれか1つの状態が選ばれてしまいます。たとえ全ての状態にたいして計算をしたとしても、観測できるのは1つだけです。これでは全ての状態について計算した意味がありません。
実際、量子コンピュータで高速に解けるアルゴリズムは数えるほどしか知られていないようです。結局、量子コンピュータで全ての計算処理が早くなるわけではありません。
シミュレータを作ってみる
少し話がながくなってしまったので、ここからは、実際にシミュレータをつくってみましょう。まずは量子ビットを表現するクラスを定義します。
量子ビット(Qubits)の定義
class Qubits(object):
def __init__(self, n_bits):
"""
Arguments:
n_bits (int): 量子ビット数
"""
self.n_bits = n_bits
self.n_states = 2**n_bits
self._amp = np.zeros(self.n_states, dtype=np.complex)
self._amp[0] = 1 # 0番目の状態の確率を1とする
def set_bits(self, bits):
"""
Arguments:
bits (list): 状態を表現するリスト ex).|0010> なら [0, 0, 1, 0]
Returens:
self (Qubits): 自分自身
"""
# 例えば |0010> が 2番目(0b0010番目) の状態に対応する
idx = sum(bit<<i for i, bit in enumerate(bits[::-1]))
self._amp = np.zeros(self.n_states, dtype=np.complex)
self._amp[idx] = 1.0
return self
def measure(self):
"""
量子ビットを観測する
Returens:
bits (list): 観測された状態を表すリスト
"""
p = np.abs(self._amp)**2
idx = np.random.choice(range(len(self._amp)), p=p)
bits = [idx>>i & 1 for i in range(self.n_bits)]
return bits[::-1]
def apply(self, *operators):
"""
量子ビットに演算子を適用する
Arguments:
operators (list): 演算子のリスト
Returens:
applied (Qubits): 演算子適用後の量子ビット
"""
amp = self._amp
for op in operators:
amp = op(amp)
applied = self.__class__(self.n_bits)
applied._amp = amp
return applied
def __str__(self):
return " + ".join(
("{}|{:0" + str(self.n_bits) + "b}>").format(amp, i)
for i, amp in enumerate(self._amp) if amp
)
__init__では、量子ビット数を指定しています。上述の通り、$2^n$の状態が存在し、それぞれに重み_ampが与えられます。初期値では0番目の状態の重みを1としていますが、set_bitsメソッドを使って変更することが出来ます。
measureでは、量子ビットを観測した結果を返します。上述のとおり、_ampの絶対値の2乗の確率で、どれか1つの状態が選ばれ、返されます。
簡単な利用例(test)は如何のとおりです。
# Tests
qubits = Qubits(5) # 5量子ビットを定義
qubits.set_bits([0, 0, 0, 1, 0]) # 4量子ビット目のみ|1>で、他は|0>
assert(len(qubits._amp) == 2**5)
assert(qubits._amp[int('00010', 2)] == 1)
assert(qubits._amp.sum() == 1)
# Test Mearure
assert(qubits.measure() == [0, 0, 0, 1, 0])
演算子の定義
次に、状態を変化させる演算子を定義します。まずはベースクラスです。
import abc
class Operator(object):
__metaclass__ = abc.ABCMeta
def __init__(self, n_bits):
self.n_bits = n_bits
@abc.abstractproperty
def matrix(self):
pass
def __call__(self, amp):
return self.matrix.dot(amp)
def __str__(self):
return str(self._matrix.todense())
量子ビットに対する操作は、$2^n\times2^n$の行列の掛け算で表すことができるので、matrixというプロパティを持つようにして、__call__で実際に掛け算するようにしています。
子クラスの1つ目はIdです。これは「なにもしない」演算子です。行列で表すと、単位行列になります。
class Id(Operator):
def __init__(self, n_bits):
super(Id, self).__init__(n_bits)
self._matrix = sp.eye(2**n_bits)
@property
def matrix(self):
return self._matrix
次にビット反転演算子 X です。
class X(Operator):
def __init__(self, n_bits, target):
super(X, self).__init__(n_bits)
self.target = target
self._matrix = sp.dok_matrix((2**n_bits, 2**n_bits))
for upper in range(2**target): # target より上位ビットをすべてなめる
for lower in range(2**(n_bits - 1 - target)): # target より下位のビットを全てなめる
idx0 = upper*2**(n_bits - target) + lower # target = 0 のインデックス
idx1 = idx0 + 2**(n_bits - 1 - target) # target = 1 のインデックス
self._matrix[idx0, idx1] = 1
self._matrix[idx1, idx0] = 1
@property
def matrix(self):
return self._matrix
すこしコードが込み入っていますが、targetの量子ビットを反転させる($\left|0\right>$を$\left|1\right>$に、$\left|1\right>$を$\left|0\right>$にする)ようになっています。n_bits=1のとき、次のような行列になります。
>>> # Test X
>>> x = X(1, 0)
>>> assert (x.matrix == np.array([[0, 1], [1, 0]])).all()
>>> print(x)
[[ 0. 1.]
[ 1. 0.]]
次にアダマール演算子Hです。
この演算子は、$\left|0\right>$や$\left|1\right>$といった純状態から重ね合わせの状態をつくることができる量子コンピュータ特有の演算子です。
class H(Operator):
def __init__(self, n_bits, target):
super(H, self).__init__(n_bits)
self.target = target
self._matrix = sp.dok_matrix((2**n_bits, 2**n_bits))
for upper in range(2**target):
for lower in range(2**(n_bits - 1 - target)):
idx0 = upper*2**(n_bits - target) + lower
idx1 = idx0 + 2**(n_bits - 1 - target)
self._matrix[idx0, idx0] = 1/np.sqrt(2)
self._matrix[idx0, idx1] = 1/np.sqrt(2)
self._matrix[idx1, idx0] = 1/np.sqrt(2)
self._matrix[idx1, idx1] = -1/np.sqrt(2)
@property
def matrix(self):
return self._matrix
n_bits=1のとき、次のような行列になります。
>>> # Test H
>>> h = H(1, 0)
>>> assert (h.matrix == np.array([[1, 1], [1, -1]])/np.sqrt(2)).all()
>>> print(h)
[[ 0.70710678 0.70710678]
[ 0.70710678 -0.70710678]]
$\left|0\right>$に作用させると、確かに重ね合わせ状態となることがわかります。
>>> qubits = Qubits(1)
>>> print('before: {}'.format(qubits))
>>> print('after: {}'.format(qubits.apply(H(1, 0))))
before: (1+0j)|0>
after: (0.707106781187+0j)|0> + (0.707106781187+0j)|1>
最後に制御Not演算子CNotです。
class CNot(Operator):
def __init__(self, n_bits, control, target):
super(CNot, self).__init__(n_bits)
self.control = control
self.target = target
self._matrix = sp.dok_matrix((2**n_bits, 2**n_bits))
for upper in range(2**target):
for lower in range(2**(n_bits - 1 - target)):
idx0 = upper*2**(n_bits - target) + lower
idx1 = idx0 + 2**(n_bits - 1 - target)
if self._get_control_bit(idx0):
self._matrix[idx0, idx1] = 1
self._matrix[idx1, idx0] = 1
else:
self._matrix[idx0, idx0] = 1
self._matrix[idx1, idx1] = 1
@property
def matrix(self):
return self._matrix
def _get_control_bit(self, bits):
return 1 & (bits >> (self.n_bits - 1 - self.control))
これは、controlが$\left|0\right>$のときは何もしないが、$\left|1\right>$のときにはtargetをビット反転させる演算子です。
>>> # Test CNot
>>> cnot = CNot(2, 0, 1)
>>> assert(cnot.matrix == np.array([[1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 0, 1], [0, 0, 1, 0]])).all()
>>> print(cnot)
[[ 1. 0. 0. 0.]
[ 0. 1. 0. 0.]
[ 0. 0. 0. 1.]
[ 0. 0. 1. 0.]]
下のコードのように、CNot演算子をつかうと、「0番目の量子ビットと1番目の量子ビットが等しい状態だけ重ね合わせる」といった複雑な重ね合わせを表現することが出来ます。
>>> qubits = Qubits(3)
>>> qubits = qubits.apply(H(3, 0), CNot(3, 0, 1))
>>> print(qubits)
(0.707106781187+0j)|000> + (0.707106781187+0j)|110>
ベルンシュタイン・ヴァジラニの問題を解いてみる
では、具体的な量子アルゴリズムを実装してみましょう。ここではベルンシュタイン・ヴァジラニの問題と呼ばれる問題を解きます。ベルンシュタイン・ヴァジラニの問題とは以下のような問題です。
ある関数 $f$ が $f(x)=x_0\cdot a_0 \oplus x_1\cdot a_1 \oplus \cdots \oplus x_{n-1}\cdot a_{n-1}$ という形であたえられているとき、$a_0, a_1, \dots, a_{n-1}$ をできるだけ少ない回数で求めよ
ちなみに、古典的な方法では、最低でもn回関数を呼び出さなければいけないことが知られています。
こういった問題は、以下の手順で解きます。
- $f(x)$を量子コンピュータで実装する
- $f(x)$をブラックボックスとして、観測値から欲しい情報が得られるような回路を実装する
では、 $f(x)$を量子コンピュータで実装してみましょう。実は、先述のCNotを使うと、とても簡単に実装できます。 例えば、 $a_0=1, a_1=0$ の場合は以下のようになります。
ここでは、0ビット目と1ビット目が入力で、3ビット目が出力に対応しています。結果をみると、0ビット目が$\left|1\right>$のときのみ、3ビット目が$\left|1\right>$となっていることがわかります。
>>> # a0 = 1 a1 = 0
>>> oracle = CNot(3, 0, 2) # ブラックボックスのf(x)のことをoracleと呼ぶ
>>> qubits = Qubits(3)
>>>
>>>
>>> for bits in ([0, 0, 0], [0, 1, 0], [1, 0, 0], [1, 1, 0]):
>>> qubits.set_bits(bits)
>>> print('{} -> {}'.format(bits, qubits.apply(oracle).measure()))
[0, 0, 0] -> [0, 0, 0]
[0, 1, 0] -> [0, 1, 0]
[1, 0, 0] -> [1, 0, 1]
[1, 1, 0] -> [1, 1, 1]
$a_0$、$a_1$の組み合わせとしては、上記以外に$(a_0, a_1)=(0, 0), (0, 1), (1, 1)$の3パターンあります。どのパターンかわからない前提で、$a_0, a_1$を当てるがベルンシュタイン・ヴァジラニの問題です。
答えから言うと、下記のようにXとHを組み合わせると良いことが知られています。
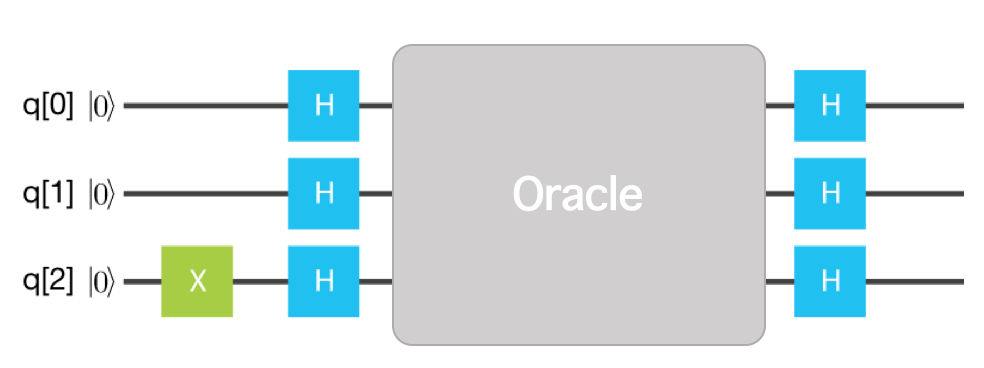
コードに落とすと以下のようになります。
def solve_bv(oracle):
n = oracle.n_bits
preprocess = ComposedOperator(X(n, n - 1), *(H(n, i) for i in range(n)))
postprocess = ComposedOperator(*(H(n, i) for i in range(n)))
qubits = Qubits(n)
return qubits.apply(preprocess, oracle, postprocess).measure()[:-1]
上記の$f(x)$に対して実行すると以下の結果が得られます。確かに1度の関数呼び出しで、$a_0,a_1$をもとめることができました。
>>> oracle = CNot(3, 0, 2)
>>> solve_bv(oracle)
[1, 0]
まとめ
ゲート方式の量子コンピュータのシミュレータをかいて遊んでみました。
それでは、Good X'math !