本記事は、量子コンピュータ Advent Calendar 2018 18日目の記事です。
量子コンピューター(ゲート方式)を使って、巡回セールスマン問題(TSP, Travelling Salesman Problem)を解くという論文を読んだので、自分の頭の整理もこめて、概要をまとめます。
| タイトル | Efficient quantum algorithm for solving travelling salesman problem: An IBM quantum experience |
|---|---|
| URL | https://arxiv.org/abs/1805.10928 |
| 概要 | 量子コンピューターを使った効率的なTSPの解法を提案し、IBM Q Experience (シミュレーター)でその一部分を実装してみた |
| 感想 | 理解が浅いためか腑に落ちない点もあるが、制御ゲートの話や量子フーリエ変換、位相推定などの話がでていたので面白かった。本当は IBM Q で実際に遊んでみたかったがそこまではいっていない。 |
循環セールスマン問題(TSP)とは
説明不要かもしれませんが、循環セールスマン問題(TSP)とは、いわゆるNPハードな問題の典型例です。

上図において、青丸の1~4が「都市」をあらわしており、それぞれの都市を繋ぐ線が「道」を表しています。$\phi_{ij}$は「都市$i$から都市$j$へ行く時の距離や時間」を表しています。単純な距離であれば$\phi_{ij} = \phi_{ji}$ですし、そうでなければ、一般には$\phi_{ij} \neq \phi_{ji}$ です。
セールスマンがすべての都市を回ってはじめの都市に戻りたいとしたときに、最短経路を求めるのがTSPと呼ばれる問題です。4都市であれば簡単ですが、$N$都市ある場合には、古典的なコンピューターでは$(N-1)!$の計算量が必要であることがわかっています。
今回の論文は、量子コンピューターを使って、(古典的なコンピューターよりも)高速にTSPを解く方法を見つけた(?)という内容です。
TSPを量子コンピューターで表現する
量子コンピューターを使うには、問題を量子コンピューター上で表現しなければいけません。そこで、まずは都市間の距離を表現する行列 $B_{ij}$ を用意します。
$$
B_{ij} = e^{i\phi_{ij}}
$$
です。このように表現しておくと、例えば$i \to j \to k$というルートを通った時の距離は
$$
B_{ij}B_{jk} = e^{i\phi_{ijk}} = e^{i(\phi_{ij} + \phi_{jk})}
$$
というふうに、掛け算の形で表せるので便利です。この $\phi_{ij} + \phi_{jk} + ...$ の部分を位相と呼びます。
一点だけ注意しないといけないのは、$e^{i(2\pi + x)} = e^{ix}$ なので、$\phi_{ij} + \phi_{jk} + ...$ と、ルートの距離を足し算していったときに$2\pi$を超えてしまうと、位相が「そのルートの距離 - $2\pi$」のものと同一視されてしまい、何を表しているのかよくわからなくなってしまう点です。
量子位相推定
さて、位相を見ることで、ルートの距離を計算できることがわかりましたので、TSPは、「位相のもっとも小さいルートを見つけ出す」問題と言い換えることができます。そこで、
- すべてのルートを量子状態として表現するアルゴリズム
- すべての状態に対して、効率的に位相を推定できるアルゴリズム
- 推定した位相から高速に最小値とそれに対応する状態を推定できるアルゴリズム
があれば、高速にTSPを解くことができそうです。(そして、この論文では2.と3.について説明しています。1.については一言「簡単だよ」と言っているだけな気がしますが、僕が薄学なため理解できていない可能性もあります)
量子フーリエ変換
「すべての状態に対して、効率的に位相を推定できるアルゴリズム」に対応するのが、量子位相推定アルゴリズムと呼ばれるものですが、そのアルゴリズムのベースとなっているのが量子フーリエ変換(QFT, Quantum Fourier Transform)です。
量子フーリエ変換については、とてもわかりやすいページがあるので、そちらを参考にしていただければと思いますが、簡単に紹介します。
まず、(量子でない)普通のフーリエ変換とは、関数を$\sin$ や $\cos$ の和で表そう、という操作のことですが、形式的には、ベクトル $x={x_{j}}$ が与えられたときに、
$$
y_{k} = \frac{1}{\sqrt{N}}\sum_{j=0}^{N-1}\exp\left(i\frac{2\pi kj}{N}\right)x_{j}
$$
というように基底を変換することであると考えることができます。これと同じことを量子コンピューターで行うのが量子フーリエ変換です。具体的には、
$$
|j> \to \frac{1}{\sqrt{N}}\sum_{k=0}^{N-1}\exp\left(i\frac{2\pi kj}{N}\right)|k>
$$
という変換を指します。$n$ビットの場合、$2^n$の状態を表せるので、$N=2^n$として
$$
|j> \to \frac{1}{\sqrt{2^n}}\sum_{k=0}^{2^n-1}\exp\left(i\frac{2\pi kj}{2^n}\right)|k>
$$
と書くこともできます。少し難しそうに見えますが、「量子フーリエ変換とはこういう変換のことを指していて、これはIBM-Qなどの量子コンピューターで実装できる」という点だけおさえておけばOKです。(すいません。Advent Calendar のため焦って書いていますので、後ほどきちんと書くかもしれません。ただ、こちらのページがわかりやすいのでおすすめです)
量子位相推定
さて、量子フーリエ変換がなぜ必要だったかというと、量子フーリエ変換の逆変換(IQFT, Inverse Quantum Fourier Transform)をつかうことで、位相を推定することができるからです(こちらも上記のサイトがわかりやすいです。)
まず、やりたいことは $U$ をユニタリ行列、$|\psi>$をその固有状態の1つとすると、
$$
U|\psi> = e^{i2\pi\phi}|\psi>
$$
となりますが、このときの$\phi$を求めることです。TSPの例では、$|\psi>$があるルートをあらわしているとすると、この$\phi$が、まさにそのルートの距離を表しているのでした。
量子コンピューターで、この$\phi$を求めるには、$\phi = \phi_12^{-1} + \phi_22^{-2} + ...$ となるような $\phi_{i} \in {0, 1}$ を求めます。
IQFTはQFTの逆変換ですから、
$$
\frac{1}{\sqrt{2^n}}\sum_{k=0}^{2^n-1}\exp\left(i\frac{2\pi kj}{2^n}\right)|k> \to |j>
$$
という変換を表しています。$j/2^n$を$\phi$と書き換えれば
$$
\frac{1}{\sqrt{2^n}}\sum_{k=0}^{2^n-1}\exp\left(i2\pi k\phi\right)|k> \to |2^n\phi>
$$
となります。$\exp\left(i2\pi k\phi\right)$を作るには、$U$を$k$回かけるだけでOKです。
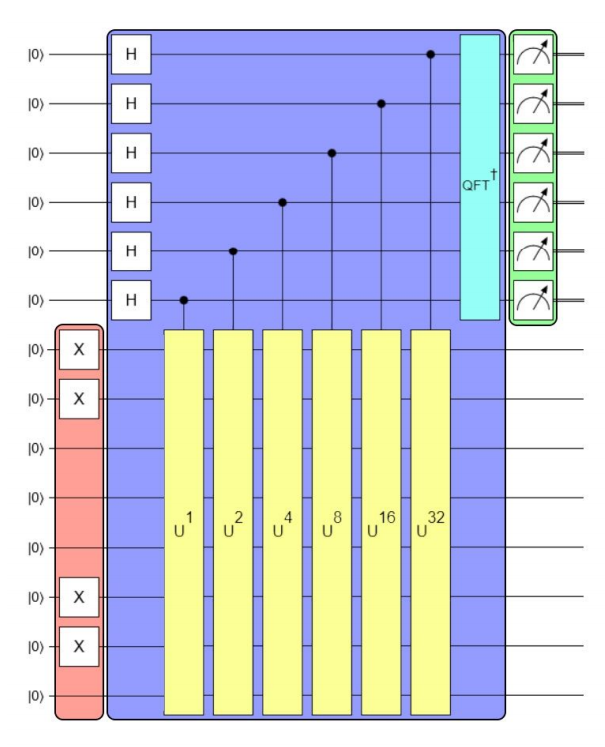
初期状態として、すべてのビットが$0$と$1$の重ね合わせ状態となっていれば、上の状態を作れるので、下図のような回路を作って、観測されたビット$2^k$しながら足し合わせることで、位相推定できることになります。(説明が雑ですいません。)$U^k$の個数は、位相を何桁目まで推定するかという
位相の最小値とそれに対応する状態を推定
論文には詳しく書いてありませんが、グローバーのアルゴリズムをベースにした、最小値推定アルゴリズムarXiv:quant-ph/9607014などを使うことができるようです。
すべてのルートを量子状態として表現するアルゴリズム
これについて論文ではきちんと言及していないように見えます。もうちょっと読み込んでみて、なにか追記できたら書きたいと思います。
まとめ(感想)
- QFTの勉強になったので、面白かった
- ただ、はじめに「すべての可能なパターンだけ」を重ね合わせる必要があるように思うが、一つ一つ重ねていくと、単純に考えて$(N-1)!$かかる気がするが、どうやって実現するつもりだろうか
- 実装してみたかった