はじめに
GNSS(GPS)を使った位置取得は、人類の大いなる進歩です!
我々はもう道に迷わないのです。(NEVER LOST AGAIN グーグルマップ誕生 なかなか面白い本でした。)
しかしながら、地図で自分の場所がわかって便利という以上のことを考えるためには、様々なこの分野特有の背景知識を必要とします。
本稿では、「高さ」というものに注目して、なんとなく常識だと思っていた概念の裏を見ていきましょう。
「高さ」という概念について
皆さんは、高さという概念について、どのようにとらえていますか?
富士山は3776mだし、東京タワーは333mでスカイツリーは634mという有名な数字は出てくる人が多いでしょう。
富士山の数字は標高の数字で、東京タワーやスカイツリーは所在地の標高からの差分なので、若干富士山の数字とは基準が違うことになります。
この基準というところが高さを考えるうえで重要になってきます。
ちなみに太陽系で最も高い山は火星のオリンポス山で、地表からの高さは実に約27000mだそうです。将来火星観光の目玉の登山になるかもしれませんね。
標高とは?
さて、改めて高さの表し方の一つ、「標高」の定義についてみていきましょう。
標高の定義
日本での標高の定義は、「東京湾の平均海水面からの高さ」です。海抜という言葉もあるように、海からの高さというのは、高さの概念の基本となります。
日本でのと書いたのは、実は国によって違う場合が多いからです。
東京湾という日本国内の基準をベースとするわけで、これが国際的に通用するものではないことは容易に想像がつきますが、
他の国も「近代的な」測地方法では、平均海水面を基準とすることが多いようです。
東京湾の平均海水面の定義をさらに詳しく見ると、
平均海水面定義(Wikipediaより https://ja.wikipedia.org/wiki/日本水準原点)
霊岸島量水標(現在の東京都中央区新川、当時の隅田川河口にあたる。)における1873年6月から1879年12月までの毎日(一時期欠測あり)の満干潮位を測定して平均値を算出し、量水標の読み(荒川工事基準面、Arakawa Peil、A.P.)で1.1344メートルを東京湾平均(中等)海面 「T.P.」(Tokyo Peil)とし、この位置をゼロメートルとして全国の標高の基準と定めた
となります。この高さを基準にして、全国の標高を測っています。
標高の測り方
では、任意の地点の標高はどのように測るのでしょうか。
標高の測量、水準測量と言っていますが、近代的な測量手法では、絶対的なその地点の標高をその地点だけで測ることができません。そのため、基準点からの相対的な高さとして求めていきます。
三角点や水準点という形で日本全国に既知でかつ定期的に測量しなおされている基準点があり、そこからの相対的な高さとして求めます。
もちろん、それぞれの基準点も基準原点・水準原点からの相対的な位置・高さになります。
水準測量は、以下の図のように水平をとれる水準器を中に置き、大きな定規のような標尺の目盛りを測ることで2点間の高さの相対値を測ります。
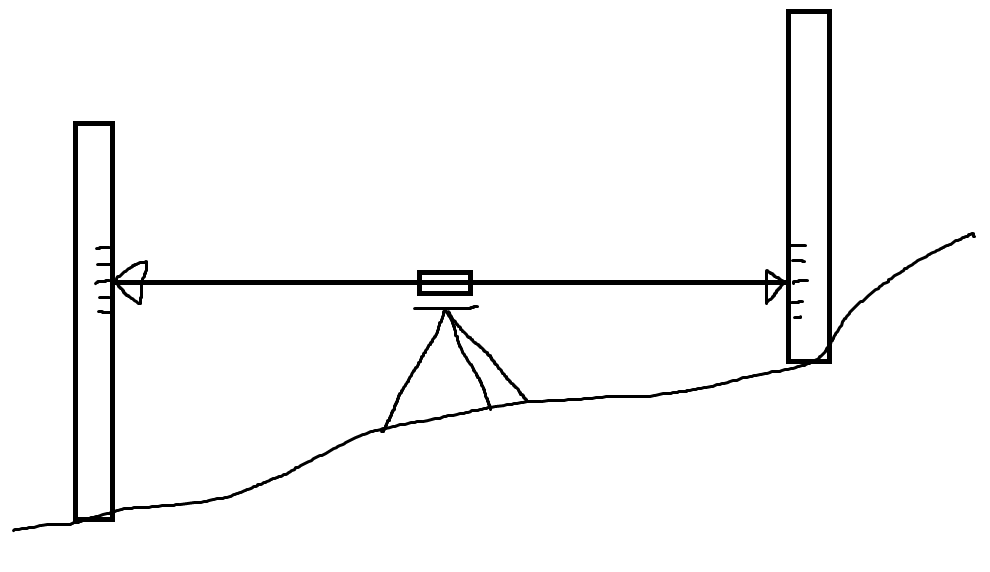
これを基準点から連続して行うことで任意地点の基準点からの相対的な高さを測るのです。
そのため、標高の基準としてどこかに必ず0mの基準が必要なのと、どう頑張ってもそこからの相対値になります。
また、長い距離があると誤差や見通せないといった問題で測量ができません。
そのため、各国ごとに標高の基準は違いました。
After GPSの世界
GPSの登場で、この状況に終止符が打たれます。これまで海水面という場所によって違う基準で測っていたものが、地球という基準をもとにして、世界中で統一された座標系で測ることができるようになりました。これ以降が今我々が享受している「現代的な」測量の世界です。
今、我々がGNSS(GPS)によって得ている座標は、世界のどこに行っても同じ基準で測られたものなのです。
素晴らしいですね。
ちなみに、このGPSによる地球基準の座標系(測地系)としてWGS84というものが決められています。このWGS84の定義の中に、後述する楕円体の定義やジオイドモデルの定義も含まれています。この測地系という概念は、地理情報系の事を扱うときにとても重要なものなので、是非覚えて帰ってください。
(とはいえ、GNSS(GPS)は深宇宙では使えません。太陽系の中での探査機の位置決定には、VLBIという方法や、光学カメラから星の位置を調べて自己位置を決定するなどのやり方があるそうです。人類が太陽系を縦横無尽に旅するような時代になったら宇宙版GPSみたいなものができるのかもしれませんね。)
楕円体高
しかし、これまでの標高という概念とGNSS(GPS)が計測する高さには大きな違いがあります。
GNSS(GPS)が測る高さは、地球を回転楕円体としてみたときのその回転楕円体表面からの高さになります。
これを楕円体高と言っていますが、この高さは標高とは違うものです。
ジオイド
そこで、標高と楕円体高を相互に関連付けるためにジオイドという概念が導入されます。
(ジオイド自体は地質学などで概念としてありましたが、衛星測位のためにより精密なモデルが作成されたそうです)
ジオイドの表面は地球の平均海水面に一致する等ジオポテンシャル面という定義なのですが、標高の基準となる平均海水面を仮想的に定義したようなものです。
このジオイド面の楕円体高からの高さがジオイド高で、地球全体でジオイド高を定義したものをジオイドモデルといいます。
そして、高さの計算は、以下の計算式で行えます。
標高 = 楕円体高 - ジオイド高
なお、ジオイドは重力と密接に関連した概念です。地球上では場所によって実は重力が微妙に違い、その違いを表しているのがジオイドという解釈もできます。水準測量のときは、水平器という液体に気泡が入った器具で水平を出すのですが、器具の仕組みとして重力的な水平を出していることになります。そのため、標高という数値は重力と紐ついているものなのでジオイドにより楕円体高から計算できている、というように自分では理解しています。
ジオイドモデル
よく地球の形を、洋ナシのような形ということがありますが、大体このジオイドモデルの形状を言っています。
単純な計算では表せない、非常に複雑な形をしています。
以下の図は、実際にEGM96のジオイドモデルをUnityで3D表示したものです。(高さ方向に引き伸ばして強調しています)
このジオイドモデルですが、重力の観測や、水準測量の結果から作成されます。日本周辺の高精度なジオイドモデルを国土地理院が整備しています。GNSS(GPS)による座標測位を補強する重要な情報であり、様々な観測の基盤情報となります。
スマートフォンにおける高さの定義
さて、ここまでは事前知識の説明です。ここから本題。
ほぼすべてのスマートフォン端末にGNSS(GPS)が組み込まれるようになり、皆さん便利に使っていますが、実はAPIで取得できる情報には大きな違いがあります。
iOSのCoreLocationでは、CLLocationで返ってくる高さはAltitudeつまり標高となります。
https://developer.apple.com/documentation/corelocation/cllocation
Androidでは、LocationのAltitudeの説明としてWGS84楕円体からの高さと定義が書いてあります。つまり楕円体高になります。
https://developer.android.com/reference/android/location/Location.html
問題点
おそらくiOSの内部では、GNSS(GPS)で取得した楕円体高から内部に持ったジオイドモデルにより標高を計算しているのでしょう。
この違いを知らずに、両方で動くアプリケーションを作ると、場合によっては高さが数十mずれたりすることにもなります。
また、iOSの方は、生のセンサー値としての楕円体高を正確には取得できないことになります。
どちらにしろ、より正確な位置情報のマルチプラットフォーム運用をしたい場合には、ジオイド高の計算を自前で持つ必要がありそうです。
ジオイド高の計算
ということで、ジオイド高を計算してみましょう。
今回は、アメリカ合衆国のNGA(国家地理空間情報局)とNASAが公開しているEGM96という少し古いジオイドモデルのデータと補間計算のプログラムを、Unityで使うことを前提にC#に移植してみました。もっとも、Unityの標準のGNSS(GPS)座標を取得する仕組みだと緯度経度がfloatで渡されて非常に残念なので、プラットフォーム側で位置情報取得してUnityに精度を維持して渡すのがよいでしょう。
元にしたデータとプログラムはこちらです。
https://earth-info.nga.mil/GandG/wgs84/gravitymod/egm96/egm96.html
https://earth-info.nga.mil
元になるプログラム
上記ページのINTPT.FというFORTRANで書かれたプログラムを元にします。
FORTRANとか久々ですね。大学の時にやはり同じような分野のプログラムを解読して以来です。
移植で苦労したのは、配列の添字の開始が1からだったところですね。FORTRANの常識として知ってはいたので注意深く書いたつもりだったんですが、いくつかバグを仕込みました。
また、数値の丸めをちゃんと指定しないと結果が同一にならないなどもありました。
コメントを見ると、元のプログラムは1996年に作成されたもので、(EGM"96”なので1996年に制定されたモデルなのでプログラムも同時期に作成されたのでしょう)ベンチマークに載っていたCDCの3文字が時代を感じさせますね。今はなきControl Data Corporationのマシンでベンチマークされています。
こういう、過去のプログラムに関わるとコンピュータ考古学みたいで楽しいですね。
なお、近い時代のコンピュータ開発のドキュメンタリとして、「超マシン誕生」という本がありますね。Windows NTの開発を描いた「闘うプログラマー」と合わせて、コンピュータ業界を描いたドキュメンタリとして有名な1冊です。
C#での移植実装
以下が補間計算のメインプログラムです。コンストラクタでArrayHのインスタンスを指定して、interpメソッドに緯度経度を与えるとジオイド高が取得できます。
using System;
using System.Collections.Generic;
using System.Text;
using System.IO;
using System.Runtime.CompilerServices;
using System.IO.MemoryMappedFiles;
namespace GeoidInterpolateLib
{
public class GeoidInterpolateEGM96
{
private const double south = -90.000000, north = 90.000000, west = 0.000000, east= 360.000000, dphi= 0.250000, dlam = 0.250000;
private const int IWINDO = 4;
public const int NBDR = 2 * IWINDO;
public const int NLAT = 721, NLON = 1441 + NBDR;
private const double DLAT = 0.25, DLON = 0.25;
private const double PHIS = south, DLAW = west - NBDR / 2 * dlam;
private const double RHO = 57.29577951;
private const double REARTH = 6371000.0;
private ArrayH H;
private const int IPA1 = 20;
private double[] A = new double[IPA1];
private double[] R = new double[IPA1];
private double[] Q = new double[IPA1];
private double[] HC = new double[IPA1];
public GeoidInterpolateEGM96(ArrayH AH)
{
H = AH;
}
public float interp(double lat,double lon)
{
double gh = interp(12.0, lat, lon);
return (float)Math.Round(gh,3,MidpointRounding.AwayFromZero);
}
[MethodImpl(MethodImplOptions.Synchronized)]
public double interp(double DMIN, double PHI, double DLA)
{
double ILIM = DMIN * 1000.0 * RHO / (REARTH * DLAT);
double JLIM = DMIN * 1000.0 * RHO / (REARTH * DLON * Math.Cos((PHIS + DLAT * NLAT / 2.0) / RHO));
double RI = (PHI - PHIS) / DLAT;
double RJ = (DLA - DLAW) / DLON;
int I0, J0;
I0 = (int)RI;
J0 = (int)RJ;
I0 = I0 - IWINDO / 2 + 1;
J0 = J0 - IWINDO / 2 + 1;
int II = I0 + IWINDO - 1;
int JJ = J0 + IWINDO - 1;
if (I0 < 0 || II >= NLAT || J0 < 0 || JJ >= NLON)
{
System.Console.Error.WriteLine("ERROR : PHI=" + PHI + " DLA=" + DLA + " STATION TOO NEAR GRID BOUNDARY - NO INT. POSSIBLE");
throw new Exception();
} else if (I0 < ILIM || II > NLAT - ILIM || J0 < JLIM || JJ > NLON - JLIM)
{
System.Console.Error.WriteLine("ERROR : PHI=" + PHI + " DLA=" + DLA + " STATION OUTSIDE ACCEPTABLE AREA - NO INT. PERFORMED");
throw new Exception();
}
for(int i = 0;i < IWINDO; i++)
{
for(int j = 0;j < IWINDO; j++)
{
A[j] = H.GetH(I0 + i,J0 + j);
}
initspA();
HC[i] = splineA(RJ - J0 + 1.0);
}
initspHC();
return splineHC(RI - I0 + 1.0);
}
private static void printArray(double[] array)
{
for(int i = 0;i < array.Length; i++)
{
System.Console.WriteLine("" + i + "\t" + array[i]);
}
}
private void initspA()
{
Q[0] = 0.0;
R[0] = 0.0;
for(int k = 1; k < IWINDO - 1; k++)
{
double P = Q[k - 1] / 2.0 + 2.0;
Q[k] = -0.5 / P;
R[k] = (3.0 * (A[k + 1] - 2.0 * A[k] + A[k - 1]) - R[k - 1] / 2.0) / P;
}
R[IWINDO - 1] = 0.0;
for (int k = IWINDO - 2; k > 0; k--)
{
R[k] = Q[k] * R[k + 1] + R[k];
}
}
private void initspHC()
{
Q[0] = 0.0;
R[0] = 0.0;
for (int k = 1; k < IWINDO - 1; k++)
{
double P = Q[k - 1] / 2.0 + 2.0;
Q[k] = -0.5 / P;
R[k] = (3.0 * (HC[k + 1] - 2.0 * HC[k] + HC[k - 1]) - R[k - 1] / 2.0) / P;
}
R[IWINDO - 1] = 0.0;
for (int k = IWINDO - 2; k > 0; k--)
{
R[k] = Q[k] * R[k + 1] + R[k];
}
}
private double splineA(double X)
{
int J = ifrac(X);
double XX = X - J;
return A[J - 1] +
XX * ((A[J] - A[J - 1] - R[J - 1] / 3.0 - R[J] / 6.0) +
XX * (R[J - 1] / 2.0 +
XX * (R[J] - R[J - 1]) / 6.0));
}
private double splineHC(double X)
{
int J = ifrac(X);
double XX = X - J;
return HC[J - 1] +
XX * ((HC[J] - HC[J - 1] - R[J - 1] / 3.0 - R[J] / 6.0) +
XX * (R[J - 1] / 2.0 +
XX * (R[J] - R[J - 1]) / 6.0));
}
public static int ifrac(double R)
{
return (int)Math.Floor(R);
}
}
}
補間用のジオイドモデルのデータとしてArrayHというインターフェースを実装した2種類のクラスを用意しています。
using System;
using System.Collections.Generic;
using System.Text;
namespace GeoidInterpolateLib
{
public interface ArrayH
{
public void LoadData(string path);
public void Dispose();
public float GetH(int i, int j);
}
}
using System;
using System.Collections.Generic;
using System.Text;
using System.IO.MemoryMappedFiles;
namespace GeoidInterpolateLib
{
public class ArrayImpl : ArrayH
{
private float[] H = new float[GeoidInterpolateEGM96.NLAT * GeoidInterpolateEGM96.NLON];
public void Dispose()
{
H = null;
}
public float GetH(int i, int j)
{
return H[j + i * GeoidInterpolateEGM96.NLON];
}
public void LoadData(string path)
{
using (var mmf = MemoryMappedFile.CreateFromFile(path))
{
using (var accessor = mmf.CreateViewAccessor(0, H.Length * 4))
{
for (int i = 0; i < H.Length; i++)
{
H[i] = accessor.ReadSingle(i * 4);
}
}
}
}
}
}
using System;
using System.Collections.Generic;
using System.Text;
using System.IO.MemoryMappedFiles;
namespace GeoidInterpolateLib
{
public class DictImpl : ArrayH
{
private MemoryMappedFile mmf;
private MemoryMappedViewAccessor accessor;
private Dictionary<int, float> hDic = new Dictionary<int, float>(100);
public void Dispose()
{
mmf.Dispose();
accessor.Dispose();
}
public float GetH(int i, int j)
{
int index = j + i * GeoidInterpolateEGM96.NLON;
float f;
if (!hDic.TryGetValue(index, out f))
{
f = accessor.ReadSingle(index * 4);
hDic.Add(index, f);
}
return f;
}
public void LoadData(string path)
{
mmf = MemoryMappedFile.CreateFromFile(path);
accessor = mmf.CreateViewAccessor(0, GeoidInterpolateEGM96.NLAT * GeoidInterpolateEGM96.NLON * 4);
}
}
}
内部のデータの持ち方として、ArrayとDictionaryで作り分けています。
これは、自分のいる場所のジオイド高を取得するなどの用途だと、地球全体のデータは必要ないので必要な部分だけ読み込むDictで、地球全域の座標データを変換する用途などの時は、あらかじめ全データを読み込んでおいた方が効率が良いのではということで、Arrayの方を使うとよいのではないかということで作り分けています。
また、ジオイドモデルのデータは、あらかじめ以下のプログラムで変換しておいて使います。
using System;
using System.Collections.Generic;
using System.Text;
using System.IO;
using GeoidInterpolateLib;
namespace DataConvert
{
class DataConvert
{
private float[] H = new float[GeoidInterpolateEGM96.NLAT * GeoidInterpolateEGM96.NLON];
private void LoadData()
{
StreamReader sr01 = new StreamReader(@"WW15MGH.GRD");
string headerLine = sr01.ReadLine();
string line;
double[] data = new double[GeoidInterpolateEGM96.NLAT * GeoidInterpolateEGM96.NLON];
int ii = 0;
while ((line = sr01.ReadLine()) != null)
{
string[] tokens = line.Split(' ', StringSplitOptions.RemoveEmptyEntries);
foreach (string token in tokens)
{
data[ii++] = double.Parse(token.Trim());
}
}
for (int i = 0; i < GeoidInterpolateEGM96.NLAT; i++)
{
for (int j = 0; j < GeoidInterpolateEGM96.NLON - GeoidInterpolateEGM96.NBDR; j++)
{
H[j + GeoidInterpolateEGM96.NBDR / 2 + (GeoidInterpolateEGM96.NLAT - i - 1) * GeoidInterpolateEGM96.NLON] = (float)data[j + i * (GeoidInterpolateEGM96.NLON - GeoidInterpolateEGM96.NBDR)];
}
for (int k = 0; k < GeoidInterpolateEGM96.NBDR / 2; k++)
{
H[k + (GeoidInterpolateEGM96.NLAT - i - 1) * GeoidInterpolateEGM96.NLON] = (float)data[GeoidInterpolateEGM96.NLON - GeoidInterpolateEGM96.NBDR - GeoidInterpolateEGM96.NBDR / 2 + k + i * (GeoidInterpolateEGM96.NLON - GeoidInterpolateEGM96.NBDR)];
H[k + GeoidInterpolateEGM96.NLON - GeoidInterpolateEGM96.NBDR / 2 + (GeoidInterpolateEGM96.NLAT - i - 1) * GeoidInterpolateEGM96.NLON] = (float)data[k + i * (GeoidInterpolateEGM96.NLON - GeoidInterpolateEGM96.NBDR)];
}
}
}
public void WriteData()
{
BinaryWriter bw = new BinaryWriter(new FileStream(@"ww15mgh.bin", FileMode.OpenOrCreate, FileAccess.Write));
foreach (float f in H)
{
bw.Write(f);
}
bw.Close();
}
static void Main(string[] args)
{
var dc = new DataConvert();
dc.LoadData();
dc.WriteData();
}
}
}
これで、iOSでは、生のセンサ値に近い楕円体高を計算できますし、Androidで標高を計算することもできるようになります。
おわりに
なぜこんなことをやっているかなのですが、ARを街中で使うときに、この辺りの計算ができると色々便利じゃないかなというところが、最初の動機になります。
さまざまな情報をより正確に扱えることは悪いことではないと思いますので、皆さんも機会があれば参考にしてみてください。
