Adversarial Examples を作るいくつかの手法についてちょっと試してみた。
Chainer 初心者なので勉強がてら、
Adversarial examples in the physical world( https://arxiv.org/abs/1607.02533 )
に記載されている Adversarial Examples を作るいくつかの手法を実装してみました。
Adversarial Examples については、下記の記事が非常に分かりやすいので、詳細な説明は省きますが、
http://sotetsuk.hatenablog.com/entry/2015/12/16/185102
http://fireflower.hatenablog.com/entry/2016/12/13/111016
予測器に対して、微小な摂動(誤認識をしやすいように作成した微少なノイズ)を加えたデータを与えて予測を行うと、ものの見事に誤認識してくれるといったものです。
Szegedy et al., Intriguing properties of neural networks. (2014) ICLR. ( https://arxiv.org/abs/1312.6199 )
Ian J. Goodfellow et al., Explaining and Harnessing Adversarial Examples ( https://arxiv.org/abs/1412.6572 )
Goodfellow "Adversarial example." (2015) Deep Learning Summer School.( http://www.iro.umontreal.ca/~memisevr/dlss2015/goodfellow_adv.pdf )
上記の例では、人間も予測器もパンダと認識できている画像(左)に対して、微少な摂動(真ん中)を加えた画像(右)をテナガザルと予測器は認識しています。人間にはパンダに見えます。
この例だと、微少な摂動で非常に確信を持った誤認識をしていますが、以前に自分が試した際は誤認識はするものの、誤認識したクラスの確率は低い状態でした。そもそも、この摂動の作り方は、対象の画像と正解のラベルを Deep Neural Network に与えて、back propagate して得られた勾配の符号(-1 or 0 or 1) にある定数を掛けたものを加えるだけ(機械学習の学習処理の際は、勾配方向と逆方向にパラメータを更新)なので、誤認識しやすくなるのは分かるのですが、誤認識するクラスの確率が高くなるというのはどうも納得できませんでした。
そんな時、Adversarial examples in the physical world をたまたま見つけ読んだところ、
上記の文献では、
It is important to note that none of the described methods guarantees that generated
image will be misclassified. Nevertheless we call all of the generated images “adversarial images”.
の通り、誤認識しやすいように摂動を加えても必ず誤認するわけでないと言っています。誤認識を保証するわけではないので、当然、誤認識したクラスの確率が高いものを保証するわけではないと思われます。
この文献では、Adversarial image を作る3つの手法が紹介されていますので、それぞれ実装して結果を比較してみたいと思います。
Adversarial image を作成する手法
- Fast Method
上記で紹介した論文で提案されている手法です。 Adversarial examples in the physical world と著書もかぶっています。
$$ \boldsymbol{X}^{adv} = \boldsymbol{X} + \epsilon sign(\nabla_{X}J(\boldsymbol{X}, y_{true}))$$
となっており、正解ラベルに対する勾配の符号を摂動として元画像に加えて、adversarial image を作っています。
def fast_gradient(chainer_model, chainer_array, eps):
target_array = Variable(chainer_array)
predict_result = F.softmax(chainer_model(chainer_array)).data
orig_ind = np.argmax(predict_result)
# create adv array
loss = F.softmax_cross_entropy(chainer_model(target_array), Variable(np.array([orig_ind.astype(np.int32)])))
loss.backward()
adv_part = np.sign(target_array.grad)
adv_array = target_array.data + eps * adv_part
return adv_array.astype(np.float32), adv_part, predict_result
2.Basic iterative method
Fast method を複数回適用する手法です。
$$ \boldsymbol{X}^{adv}_0 = \boldsymbol{X} $$
\boldsymbol{X}^{adv}_{N+1} = Clip_{\boldsymbol{X},\epsilon}\{\boldsymbol{X}^{adv}_N + \alpha sign(\nabla_{X}J(\boldsymbol{X}^{adv}_{N}, y_{true}))\}
Clip_{\boldsymbol{X}, \epsilon}\{ \boldsymbol{X}'\}(x,y,z) = min\{ 255,\boldsymbol{X}(x,y,z)+\epsilon,max\{0, \boldsymbol{
X}(x,y,z)-\epsilon,\boldsymbol{X'}(x,y,z) \} \}
iteration 毎に clip 処理を入れて、結果として各ピクセルへ加える摂動の範囲は、$-\epsilon$ から $\epsilon$ に抑えています。また、論文内では、$\alpha=1$ 、iteration の回数は、$ min(\epsilon + 4, 1.25 \epsilon)$ としています。
def iterative_gradient(chainer_model, chainer_array, eps, alpha):
adv_images = np.copy(chainer_array)
predict_result = F.softmax(chainer_model(chainer_array)).data
orig_ind = np.argmax(predict_result)
iter_num = int(min(eps + 4, 1.25 * eps))
print("iteration_number {}".format(iter_num))
for _ in range(iter_num):
adv_images = Variable(adv_images)
loss = F.softmax_cross_entropy(chainer_model(adv_images), Variable(np.array([orig_ind.astype(np.int32)])))
loss.backward()
adv_part = np.sign(adv_images.grad)
adv_images = adv_images.data + alpha * adv_part
adv_images = np.clip(adv_images, chainer_array - eps, chainer_array + eps)
return adv_images.astype(np.float32), adv_part, predict_result
3.Iterative least likely class method
上記2つの手法は、間違ったクラスの情報を使用せず、正しいクラスに対するコストを増加させるような手法です。これらは、みんな大好き MNIST や CIFAR10 など、分類対象のクラスの数が高々 10 と少なく、各クラスの特徴が明らかに異なっているような場合は効果的だが、ImageNet など分類対象のクラスが多いような問題だと、誤認識の仕方がいまいちな場合がある。例えば、あるソリ犬(breed of sled dog)を別のソリ犬と認識するなど。と論文では述べられている。
パンダをテナガザルというような間違いではなく、見た目が似ている別のクラスと認識したり、出力する確率は低いが正解クラスと認識するようなことが起こりやすいということだと理解しています。
このような問題に対応するために、正解クラスを与えた際の勾配を加えるのではなく、予測器が最も低い確率を出力するクラスを与えた際の勾配を引く、要するにそのクラスの方に予測されやすくなるように摂動を与える手法になります。
y_{LL} = \arg\min_{y}\{p(y|\boldsymbol{X})\}
$$\boldsymbol{X}^{adv}_0 = \boldsymbol{X}$$
\boldsymbol{X}^{adv}_{N+1} = Clip_{\boldsymbol{X},\epsilon}\{\boldsymbol{X}^{adv}_N - \alpha sign(\nabla_{X}J(\boldsymbol{X}^{adv}_{N}, y_{LL}))\}
$\alpha$, iteration 回数は、上記の iterative method と同じ値を論文中では設定しています。
def iterative_least_likely(chainer_model, chainer_array, eps, alpha):
adv_images = np.copy(chainer_array)
predict_result = F.softmax(chainer_model(chainer_array)).data
least_ind = np.argmin(predict_result)
iter_num = int(min(eps+4, 1.25*eps))
print("iteration_number {}".format(iter_num))
for _ in range(iter_num):
adv_images = Variable(adv_images)
loss = F.softmax_cross_entropy(chainer_model(adv_images), Variable(np.array([least_ind.astype(np.int32)])))
loss.backward()
adv_part = np.sign(adv_images.grad)
adv_images = adv_images.data - alpha * adv_part
adv_images = np.clip(adv_images, chainer_array - eps, chainer_array + eps)
return adv_images.astype(np.float32), adv_part, predict_result
実験
今回は、caffe で学習済みの Alexnet を chainer 用に変換して利用しています。
Alexnet は、ImageNet 用に学習されているもので、400 クラスの分類を対象としています。
$\epsilon$ の値については $\epsilon=8$ としています。かなり大きな値のように思えますが、後述しますが論文中でも $\epsilon$ の値は大きいです。
とりあえず、パンダを認識させてみる。
predict_original_image: 'giant panda, panda, panda bear, coon bear, Ailuropoda melanoleuca', predict_prob: 0.614875078201294
ちゃんとパンダと認識しています。
それでは3つの手法の結果をみてみましょう。
- Fast method
predict_adversarial_examples: 'giant panda, panda, panda bear, coon bear, Ailuropoda melanoleuca', predict_prob: 0.027273619547486305
パンダの白い部分がなんとなくもやっとしています。パンダと認識はしていますが、確度はかなり低いです。論文通り。
- Iterative method
predict_adversarial_examples: 'Shih-Tzu', predict_prob: 0.3308559060096741
見た目は Fast method とほとんど変わらないですね。
犬のシーズーと認識しています。パンダではないですが、まぁパーツの色合いは似てるってとこですね。これも論文通り。
- Iterative least likely class method
least likely category 'hot pot, hotpot'
predict_adversarial_examples: 'hot pot, hotpot', predict_prob: 0.3041199743747711
見た目は、他に比べてオリジナル画像(clean image)に近い?
結果は、見事に最も確率の低い火鍋と予測してますね。当然パンダとは全く異なるものです。中国と関連がありそうってコンテンツって意味では似ているかもしれない(適当)。
見事に論文通りの結果となってめでたしめでたしです!
コードはこちらにあります。https://github.com/ohnabe/adversarial_examples
RGB を GBR にしたり、CWH を HWC にしたり逆にしたり、chainer と caffe の仕様の違いやらがめんどくさかったです。
caffe のモデルを chainer に変換する部分は、こちらを参考にしました。ありがたや。
https://qiita.com/tabe2314/items/6c0c1b769e12ab1e2614
ε について
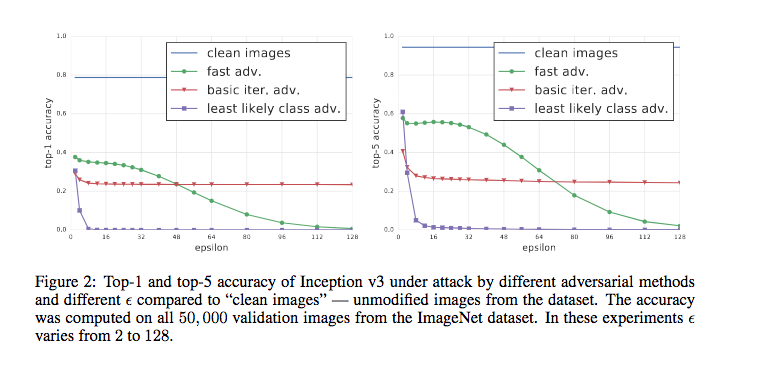
実験で設定した $\epsilon$ の値については、Ian J. Goodfellow et al., Explaining and Harnessing Adversarial Examples で出されているような、0.07 などではないです。論文中では、$\epsilon$ の値と認識性能についての評価を行っていて、そのときの値がこんな感じだったので今回は論文のスケールに合わせています。
$\epsilon >= 8$ で 、least likely class method が急激に認識精度が低下しています。$\epsilon$ の値を小さくすると、iteration や $\alpha$ の値も変わりそうですが、この辺はまた調査したいと思います。