IBM Quantum Challenge 2020 にチャレンジしてみた ～量子プログラミング入門～

目次

0. まえがき
1. はじめに
2. IBM Quantum Challenge 2020
3. 環境構築
4. Qiskitライブラリのイロハ
5. Week 1-a: 全加算器を作る
6. Week 1-b: グローバーのアルゴリズムの基礎
7. Week 2-a: ライツアウトパズルを解く
8. Week 2-b: 複数のライツアウトパズルを一気に解く
9. Week 3: 最終問題
-1. おわりに

##0. まえがき

この記事は量子計算に興味のある方に向けて書かれています。
特に、コンペの過去問としてIBM Quantum Challenge 2020 を解いてみたい方に、私の体験を共有することでよりハードルを低くできれば本望です。

なお、

• 量子ビットやXゲート、Hゲートなどの量子演算などの概念(下記参考文献を参照)
• pythonの書き方

の基本的な知識は前提として進めます。

##1. はじめに

こんにちは。
ohkenです。

量子コンピュータ、最近よく話に聞くという方も多いかと思います。

よく「量子コンピュータ」と呼ばれるものには

• アニーリング方式
• ゲート方式

と大きく二つの種類があります。
アニーリング方式は特に組み合わせ最適化への応用の有効性が期待されており、D-Wave社により商用化された計算機で採用されたことで大きな話題となりました。
アニーリング方式のコンピュータは最適化問題を解くことに特化した計算機である一方、ゲート方式は「古典コンピュータにおける計算を原理的にすべて実現可能」という意味で汎用コンピュータと呼ばれています。
ゲート型の量子計算機はIBMが積極的に開発・商用化したことで知られています。

こうした広がりを受けて、量子計算に興味を持つ方も増え、様々な良い教材へのアクセスもそれなりに充実してきています。
例えば、入門サイトとして有名なものに

• Quantum Native Dojo

があります。
また、量子計算による機械学習の実現も多くの人の興味を引く分野であり、

• 量子コンピュータによる機械学習

が(おそらく初めて)まとまった教科書として昨年発売されました。

一方、これらの読み物を通して量子計算の理論を勉強しても、なかなか実際に量子プログラミングをする機会がありません。
そのため、学んだアルゴリズムを実装レベルで理解することはいまだややハードルが高いとも言えます¹。

そこでこの記事では、特にゲート方式の量子コンピュータにおけるアルゴリズムの実装方法、およびその周辺のライブラリ(Qiskit)の使い方を、以前のコンペの問題の解法を通して学んでいく過程を紹介したいと思います。

##2. IBM Quantum Challenge 2020

今回扱った題材は、表題のコンペです。
IBMは自社でゲート型量子コンピュータの開発をしていることから、これをより広めていく活動の一環として量子プログラミングのコンテストを2019年から行っています。
2019年の第1回の後、2020年には5月、11月の二回行われました。
2021年5月には第4回のコンペが行われました。

今回取り組んだのは、第3回のコンペです。

ここで扱う量子アルゴリズムの範囲を先に書いてしまうと

• グローバーのアルゴリズム
• QRAM

です。
この記事では主に実装周りに関して調べたことなどを書いていくので、理論についての説明は特にしません。
理論的な部分は実際の問題文中での解説や前述のQuantum Native Dojo (量子探索アルゴリズム)を読むのがよいと思います。
(コンテスト問題文の解説だけでもコンパクトにわかりやすく書かれています)

課題は全部で4つの週(Week 0 ~ 3)から成り、各週で1~2個の問いが用意されています。

それでは、実際に解いてみたときにやったことを順番に書いていきたいと思います。
なお、基本的にはコンテストの問題文だけでほとんど必要な情報が十分に得られるようになっていますので、本記事では重複する内容はあまり書かず、内容を補完するものとして学習をサポートすることを目指します。

##3. 環境構築

早速やっていきたいのですが、まずは環境構築をしなければなりません。
環境構築、最初の壁ですよね…
何も知識がないと、一文字もコードを書けずにここで挫折してしまうという初心者殺し感。

でも今回使うQiskitはとても簡単な方です。
Qiskit(キスキットと読むようです)は、IBMが自社で開発する量子コンピュータで使うために開発しているライブラリです。
古典コンピュータでも全く同じインターフェースでシミュレータを走らせることができるため、IBMのシステムを動かすのと同じコードで開発していくことができます。

それでは、公式サイトの案内に従ってpipでインストールしてみましょう。
Anaconda上でのインストールが推奨されています。
pipをAnacondaを使うのは不安…という方は仮想環境を立てるのがよいです。
また、演習内で量子回路の描画を行うため、visualizationオプションをつけてインストールするのがよいでしょう。

pip install qiskit[visualization]

(Macではクォーテーションをつけて'qiskit[visualization]')
で完了です。

ちなみに、Week0ではコードを書くことなく、より直感的に量子プログラミングを行うデモができるようです。
量子回路に全く触れたことがない方はこちらを見てみるのもよいでしょう。

##4. Qiskitライブラリのイロハ

コンペの問題に入っていく前に、これから使うライブラリの仕様を少し眺めてみます。

Qiskitを使ったプログラミングは大きく二つのフェーズから成ります。

1. 回路の構成
2. 回路の実行(シミュレーション)

1の回路構成は、量子ゲートを組み合わせて構築していきます。
量子プログラミングの本丸であり、ここにアルゴリズムを組み込んでいくことになります。

2の回路の実行は書いて字のごとく、シミュレータ(or 量子計算機実機)を回路通りに走らせます。
ここはやることはだいたい決まってるので変更することはほとんどないです。

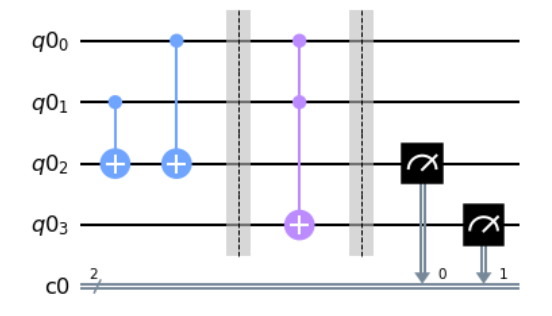
Week 1で出てくる半加算器のサンプルコードを見てみましょう。

from qiskit import QuantumRegister, ClassicalRegister, QuantumCircuit
from qiskit import Aer, execute

#各レジスター、量子回路を宣言
q = QuantumRegister(4)
c = ClassicalRegister(2)
qc = QuantumCircuit(q,c)

#XOR
qc.cx(q[1], q[2])
qc.cx(q[0], q[2])
qc.barrier()

#AND
qc.ccx(q[0], q[1], q[3])
qc.barrier()

#Sum
qc.measure(q[2], c[0])
#Carry out
qc.measure(q[3], c[1])

backend = Aer.get_backend('qasm_simulator')
job = execute(qc, backend, shots=1000)
result = job.result()
count = result.get_counts()
print(count)
qc.draw(output='mpl')

一つ一つの命令はおいておき、主なクラスとメソッドをここでまとめておきます。
詳しい使い方は問題を解きながら見ていきましょう。

回路の構成

• QuantumRegister、ClassicalRegister クラス
  • それぞれ量子ビット、古典ビットに対応する。
  • 初期化の引数はビット数
  • $|0\rangle$で初期化されている
  • q[0], c[:3]のようにスライスで指定できる
• QuantumCircuit クラス
  • 量子回路を表す
  • 初期化はQuantumRegister及びClassicalRegisterを引数に取る
  • 量子ゲートや観測(measure)はこのクラスのメソッドとして実装されている

回路の実行

• Aer (BasicAer, IBMQ)パッケージ
  • 実行するシミュレータ(IBMQは実機)
  • 引数で詳細なシミュレータの条件を決める(このあたりはよくわかってないです)
• execute
  • 量子回路をコンパイルして実行する
  • 回路、バックエンド、実行回数を引数に取る
  • 実行条件と結果をもったjobオブジェクトを返し、それぞれjob.status、job.resultで取得できる

ちなみに最後のqc.drawで構成した量子回路を可視化することができます。

以上で、なんとなく量子計算機を扱うインターフェースのイメージがつかめたでしょうか。
より詳しくはこちらを読むとよいかと思います。

##5. Week 1-a: 全加算器を作る

注意：以降では、解答およびそのヒントなどのネタバレを各節の最後に書きます。これから問題を解かれる方はまず問題のページをみて取り組まれることを推奨します。

それでは、ようやく演習に入っていきましょう。

week-1 exercise 1aでは、最も基本的な古典計算である加算器を実装していきます。

ぼく「加算器か…大学1年の情報の授業でよくわからないまま作ったな…」

という思い出に浸りつつ、まぁ楽勝やろ、と取り組んでみます。

まずはいろんなゲートに触りつつ…

…

…ふむ、アルファベットが多すぎてどれが何だか覚えられん。
(ちなみにこのときの私の量子コンピュータに関する知識レベルは「量子状態はユニタリ行列で操作できるらしい(どうやるのかは全く知らん)」という感じで、パウリ行列、アダマールゲートと言われてもパッと浮かばないくらいです)

終わった後から考えると、X、H、CXだけきちんと覚えればだいたい事足ります。

• Xゲート(NOTゲート)
  • ビットの01を反転します。

X=
\begin{pmatrix}
0 & 1 \\
1 & 0
\end{pmatrix}

• Hゲート(アダマールゲート)
  • ビットの重ね合わせ状態を作ります。重ね合わせを制するものは量子計算を制す。

H=
\frac{1}{\sqrt 2}
\begin{pmatrix}
1 & 1 \\
1 & -1
\end{pmatrix}

• CXゲート(Control NOTゲート)
  • 制御ビットとターゲットビット上のゲート。制御ビットが1のときターゲットビットの01を反転(=Xゲート)する。
  • 要はif文を表現する

CX=
\begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 \\
0 & 0 & 1 & 0
\end{pmatrix}

(2×2のブロックで見たときに左上が制御ビット、右下がターゲットビットへの作用)

CXの拡張としてCCXも重要です。

• CCXゲート(Toffoliゲート)
  • 2つの制御ビットを持つ制御NOTゲート (両方が1のときに反転を行う)

CCX=
\begin{pmatrix}
1 & 0 & 0 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 1 \\
0 & 0 & 0 & 0 & 1 & 0
\end{pmatrix}

CCXゲートはその定義から、単体でANDゲートを表現できます。
古典計算はすべてNOTゲートとANDゲートの組み合わせに帰着できることは良く知られています。
なので、これで古典計算が量子計算機でもできることがわかりました。

問題文で解説されている半加算器の説明を読んで、全加算器を作りにいきます。

まずは解答コードを検証できるよう、テストコードを作りましょう。
というのも、コンテストの本番では運営側の用意した検証用コード(ここではgrade_ex1a)がおそらくコンテスト用の環境にしか実装されておらず使えないためです。

テストコードを書いてみるのも勉強になりました。
以下に(あまり綺麗とは言えませんが)作ったものを載せておきます。

def grade_ex1a(qc):
    """
    Input: QuantumCircuit qc
    Output: boolean
    8通り全てで正しい答えを返す場合True, それ以外False
    """
    num_qubits = len(qc.qubits)
    num_clbits = len(qc.clbits)
    answer = {
        '000': {'00': 1000},
        '001': {'01': 1000},
        '010': {'01': 1000},
        '100': {'01': 1000},
        '011': {'10': 1000},
        '110': {'10': 1000},
        '101': {'10': 1000},
        '111': {'11': 1000}
    }
    for query, ans in answer.items():  
        q_init = QuantumRegister(num_qubits)
        init_circ = QuantumCircuit(q_init, ClassicalRegister(num_clbits))
        for i in range(3):
            if query[i]=='1':
                init_circ.x(q_init[i])
        test_qc = QuantumCircuit.compose(init_circ, qc)
        backend = Aer.get_backend('qasm_simulator')
        job = execute(test_qc, backend, shots=1000)
        result = job.result()
        count =result.get_counts()
        if count != ans:
            return False
    return True

print(grade_ex1a(qc))

• 古典計算⇒決定的なアルゴリズムなので、実行回数(1000)が正解の観測回数({'00': 1000}など)と等しくなるようにしました
• 初期状態(デフォルト'000')を変更してテストするため、Xゲートで各ビットを反転したものを実行しました
  • その際、「前にゲートを追加する」方法として「初期化用の回路を作って.composeで結合する」方法をとりました(もっと素直にやる方法あるのだろうか)

解答

この問題は完全に古典計算の範疇ではありますが、普通に苦戦してしまったのでちゃんと書いておこうと思います…笑
しばらくゲートをごちゃごちゃやって混乱して、数日寝かせてから考えたらすっきりわかりました。

3ビットの入力から2ビットの出力を返すので理想的には5ビットでできると良いです。

方法1: 半加算器を使う

q = QuantumRegister(5)
c = ClassicalRegister(2)
qc = QuantumCircuit(q,c)

# 半加算器
#XOR
qc.cx(q[1], q[3])
qc.cx(q[0], q[3])  # q[3]が半加算器の出力S
#AND
qc.ccx(q[0], q[1], q[4]) # q[4]が半加算器の桁上げ出力C
qc.barrier()
# ここまで半加算器

# 半加算器の出力S = X = 1 なら半加算器の桁上げ出力Cを反転 → q[4]が桁上げ出力
qc.ccx(q[2], q[3], q[4])

# Xが1ならSを反転 → q[3]が出力
qc.cx(q[2], q[3])

qc.measure(q[3],c[0])
qc.measure(q[4],c[1])

ここでccxというのは、二つのコントロールビットを持つ制御NOTゲートです。
ちなみにqc.barrier()は描画の際に区切り線ができてモジュールの単位がわかりやすくなるもので実質的な機能はたぶんないです。

方法2: 「足す1」を一般的に実装する

入力の3ビットは順番が結果に関係ありません。
ですのでそれを踏まえた統一的な書き方をしてみることもできます。

2ビットの数 $b_1b_2, b_1,b_2 \in \{0,1\}$ について、1を足すことは

1. $b_2$が1ならば$b_1$を反転する
2. $b_1$を反転する
   という操作で実現できるはず。

入力ビット$b$が1ならばこれを行い、0ならば何もしなくてよいのだから、これは制御NOTゲートを使えば実現できる！
これで作った全加算器を以下に示します。

q = QuantumRegister(3)
ans = QuantumRegister(2)
c = ClassicalRegister(2)
qc = QuantumCircuit(q,ans,c)

def add(s):
    # qubit s をansに足す
    qc.ccx(ans[0], s, ans[1])
    qc.cx(s, ans[0])

for i in range(3):
    add(q[i])

qc.measure(ans,c)

本質的にはさっきのコードと同じことをしていますが、統一的に書けて少し綺麗に見えます。

ゲート数を減らすことを考えれば一回目のccxは冗長ですが、そういった最適化はまず問題を解ききってから考えるのが鉄則です。

##6. Week 1-b: グローバーのアルゴリズムの基礎

Week 1-bではグローバーのアルゴリズムについて学びました。
(補足：IBM Challenge 2020ではグローバーがメイン課題でしたが、2021の回では量子フーリエ変換や量子誤り訂正なども扱われているようです。そちらもやってみたい)
演習問題では、グローバーのアルゴリズムの最適な反復回数を求めます。

グローバーのアルゴリズムは、データベースからクエリにヒットするデータを効率的に探索するアルゴリズムです。
実装のみに注目して、必要なのは次の2ステップだけです。

1. 「オラクル」を実装する
2. Diffusionを行う

この2ステップをデータの重ね合わせ状態に適当な回数適用することで、状態がいつの間にかほしいデータに変化しているという摩訶不思議なアルゴリズムです！

今、データ $\{|1\rangle,|2\rangle,\cdots, |N\rangle\}$ からあるクエリにヒットするものを見つけたいとします。
(初期化として重ね合わせ状態$\sum_{i=1}^N |i\rangle$を準備しておきます)

このとき、オラクルは追加の1量子ビット $|c\rangle$ を使って次のようなユニタリ変換として書かれます²。

|i\rangle |c\rangle \mapsto 
\left\{
\begin{array}{ll}
-|i\rangle |c\rangle & i \text{がクエリにヒット} \\
|i\rangle |c\rangle & \text{otherwise}
\end{array}
\right.

このような操作は、最初に $|c\rangle = |0\rangle$ にXゲートとHゲートを作用させておいて

|c\rangle = |-\rangle := \frac{1}{\sqrt 2} (|0\rangle - |1\rangle)

としておくことで実現できます。
$|-\rangle$ にXゲートを作用させると $|-\rangle \to -|-\rangle$ と変化するので、クエリにヒットしたことを示す補助ビットを用いて制御NOTゲートを$|c\rangle = |-\rangle$ にかけてあげれば先のユニタリ変換が実現できるわけです。
(言葉でいうと少しややこしいですし、実際この補助ビットをうまく構成するのが一番難しいところになります。詳しくはサンプルコードを見るのが良いでしょう)

二番目のdiffusionについては、以下を実行するだけで良いです。

data = QuantumRegister(n)  # データを表すビット(先の例ではN=2^nに対応) 
ancilla = QuantumRegister(d)  # mctで使う補助ビット
glover_iteration = 10  # グローバーの反復回数

...(初期化など)

for _ in range(glover_iteration):

    ...(oracle)

    # diffusion
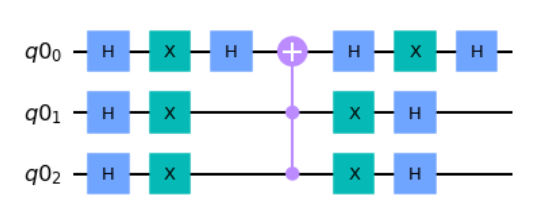
    qc.h(data)
    qc.x(data)
    qc.h(data[0])
    qc.mct(data[1:],data[0],ancilla)
    qc.h(data[0])
    qc.x(data)
    qc.h(data)

ここでmctは任意の長さの制御ビットによる制御NOTゲートです(data[1:]がすべて1ならdata[0]を反転する)。
ancillaはこの関数で必要とされる補助ビットで、mct前後で状態は変化しません。

この図では $n=3$ なのでmct(data[1:],data[0],ancilla)はccx(data[1],data[2], data[0])と同じです。

理論的にはこのdiffusionのステップがグローバーのアルゴリズムの肝で理解が大変なところですが、実装としては何も考えずにこれを実行してしまえばよいです。
(なぜこれでうまくいくかはコンペの解説文などを参照してください。)
オラクルがイメージしやすいけれど実装が大変なのと対照的ですね。

解答

と、ここまで理解すれば演習問題は簡単です。
(というより、ここまで理解しなくてもサンプルコードをいじるだけで答えを知るためのコードは書けてしまいます…！)

$n=4$ の場合に最適な反復回数を知るためのサンプルコードが与えられているので、これを $n=7$ の場合に書き換えてあげればよいです。
このときmctに使う補助ビット数を少し大きくしておくことを忘れないようにしましょう！

これでグローバーで解を高確率で得るための最適な反復回数がわかりました³。

##7. Week 2-a: ライツアウトパズルを解く

お次の演習はWeek 2-aです。

ライツアウトパズル、ご存じでしょうか？

この演習を一緒に行った友人は、半分以上知りませんでした⁴。
やったことのない人は例えばこのサイトでポチポチ遊んでみましょう

この課題では3×3のライツアウトをグローバーのアルゴリズムを使って解きます。

探索空間は3×3=9ビットあれば十分です。
(解き方はスイッチを押す順番によらないので、各スイッチを押したかどうかだけで解が決まります)

先の内容を踏まえれば、オラクルの組み方を頑張ってうまく作れれば解けることになります。

…それを考える前に、またテストコードを作っておきましょう！
本来用意されていたprepare_ex2a関数をできるだけ再現するようこんな感じにしてみました

'''
def week2a_ans_func(lights):
    ...
    return qc

を実行したあとに↓を実行
'''
from qiskit import Aer
def prepare_ex2a(func, lights=[0, 1, 1, 1, 0, 0, 1, 1, 1]):
    '''
    input :
        func : lights -> qc の関数(解答欄で作るやつ)
        lights : パズルの盤面
    output :
        qiskit.execute関数が返すjobのインスタンス
    '''
    backend = Aer.get_backend('qasm_simulator')
    qc = func(lights)
    return execute(qc, backend=backend, shots=1000, seed_simulator=12345, backend_options={"fusion_enable":True})

lights = [0, 1, 1, 1, 0, 0, 1, 1, 1] # 好きなパズルを設定する
job = prepare_ex2a(week2a_ans_func, lights)

result = job.result()
count = result.get_counts()
# ↓の一行は公式で用意している関数とのズレを合わせるため
count = sorted(count.items(), key=lambda x:x[1], reverse=True)

original_problem_set_counts = count[0]

# 最も観測回数の多いビット列が解として扱われます
# (解のビット列, 回数(1000回中))の形式
print(original_problem_set_counts)

ちなみに、問題文中で「使う量子ビットは28ビットまでに抑えること」とありますが、現在のqiskit(というかバックエンド)の仕様としてそれくらいのビット数しか扱えないようです。
ここでは一応30ビットまで使える(らしい)Aerバックエンドを用いています。

また、これで得られた解がちゃんと答えになっていることを確かめるためのコードも作りました。

def sol2light(solution):
    lights = [0] * 9
    for i in range(3):
        for j in range(3):
            if solution[3*i+j]='1':
                for (x,y) in [(-1,0), (0,-1), (0,0), (1,0), (0,1)]:
                    if i+x in range(3) and j+y in range(3):
                        lights[3*(i+x) + (j+y)] = 1 - lights[3*(i+x) + (j+y)]
    return lights

# この出力が元のパズルと一致していればok
print(sol2light(original_problem_set_counts[0]))

なお、普通に量子回路を組むと出てくる答えのビット順が想定の逆になっていることが非常に多くあります。
Week 1-aの問題文にもちょろっと書いてありますが、これは観測結果で表示されるビット列が宣言した QuantumRegister インスタンスのビット順と逆順になるからです。

例：q = QuantumRegister(3) -> 観測結果: 'q[2]q[1]q[0]'

これは答え合わせの時に混乱しがちなので十分気を付けてください。

解答

それでは解答に入りましょう。
ちなみに、ここで紹介する解答よりもずっと効率の良い解き方があります。
公式Githubのsolutionページから見られますので、自分で解いた後で読んでみることをぜひお勧めします。

ここでのオラクルには、盤面を表す9ビットを補助ビットとして使いましょう。
解の重ね合わせに対して解けるかどうかのオラクルを返すためには、解のビットで盤面を操作(制御)して、すべてのライトが消えていることをNOT + 制御NOTで確認してあげればよいことになります。
(と言いつつ、下の実装では盤面全体でのxorを計算しています⁵)

def week2a_ans_func(lights):    
    num_qubits = 28
    num_iter = 1
    
    q = QuantumRegister(num_qubits)
    c = ClassicalRegister(9)
    qc = QuantumCircuit(q, c)

    # 全てのスイッチの通りの重ね合わせを作る
    qc.h(q[:9])
    
    # oracle bit(クエリにヒットする場合に位相反転するビット)を初期化
    qc.x(q[27])
    qc.h(q[27])
        
    def switch(i,j):
        q_sub = QuantumRegister(num_qubits)
        c_sub = ClassicalRegister(9)
        qc_sub = QuantumCircuit(q,c)
        for (x,y) in [(-1,0), (0,-1), (0,0), (1,0), (0,1)]:
            if i+x in range(3) and j+y in range(3):
                qc_sub.cx(q[3*i + j], q[9 + 3*(i+x) + (j+y)])  # 補助ビット9個にスイッチ(i,j)に対応する盤面を書き込む
        return qc_sub
    
    for _ in range(num_iter):
        for i in range(3):
            for j in range(3):
                qc = QuantumCircuit.compose(qc, switch(i,j))

        # oracleを作る
        # 「盤面(補助ビット)が一致しているときだけ1を返すビット」を作る

        # 盤面の各ビットのxorをとる (一致しているときだけすべて0になる)
        for i in range(9):
            if lights[i]:
                qc.x(q[9 + i])
        # 盤面全体でorをとる
        qc.cx(q[9], q[18])
        qc.cx(q[10], q[18])
        qc.ccx(q[9], q[10], q[18])
        for i in range(1,9):
            qc.cx(q[10 + i], q[18 + i])
            qc.cx(q[17 + i], q[18 + i])
            qc.ccx(q[10 + i], q[17 + i], q[18 + i])
        qc.x(q[26]) # 盤面が一致したときだけq[26]に1が立つ

        # 28ビット目で位相反転
        qc.cx(q[26], [27])

        # 上の操作を全部戻す
        qc.x(q[26])
        for i in range(8,0,-1):
            qc.ccx(q[10 + i], q[17 + i], q[18 + i])
            qc.cx(q[17 + i], q[18 + i])
            qc.cx(q[10 + i], q[18 + i])
        qc.ccx(q[9], q[10], q[18])
        qc.cx(q[10], q[18])    
        qc.cx(q[9], q[18])
        for i in range(8,-1,-1):
            if lights[i]:
                qc.x(q[9 + i])

        for i in range(3):
            for j in range(3):
                qc = QuantumCircuit.compose(qc, switch(i,j))

        # diffusion
        qc.h(q[:9])
        qc.x(q[:9])
        qc.h(q[8])
        qc.mct(q[0:8], q[8], q[9:18], mode='basic')
        qc.h(q[8])
        qc.x(q[:9])
        qc.h(q[:9])
    
    # ビットを逆順で観測 
    qc = qc.reverse_bits() 
    qc.measure(q[-9:],c)

    return qc

注意として、オラクルのための補助ビット(=盤面のビット)はオラクルを呼び出した後もとに戻してください。
これはオラクルのユニタリ変換を忠実に表現するために必要なことです。

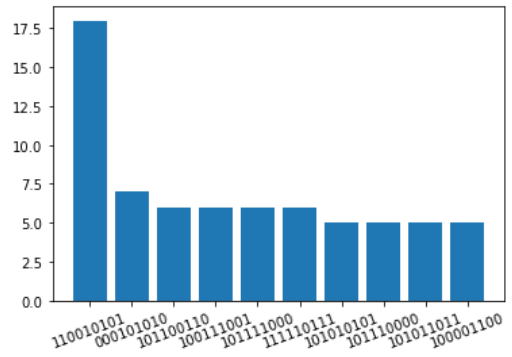
これをシミュレータで実行して、観測するビット列のヒストグラムをとってみるとこんな感じになります。
縦軸は1000回中観測された回数です。

ここでは反復回数を1回にしているので高確率というほどではありませんが正しい解が出る確率がちゃんと高くなっていることがわかります。
9ビットの場合17回が最適な反復回数です。
反復回数を17回にしてほぼ100%正しい解が観測できることをぜひ確かめてください。

##8. Week 2-b: 複数のライツアウトパズルを一気に解く

このあたりから、だんだん難易度が上がってきます。
本題とはそれますが、少ない問題数でこれだけ自然にステップアップできる問題構成を練り上げるのはさぞ大変だっただろうなぁと思います。
教育的なプログラムを作る方には心から畏敬の念を感じます。

閑話休題。

Week 2-bでは複数のパズルを一気に解くことが課題となります。
具体的には、押せるスイッチの個数に制限がある中で解けるパズルを見つけることがゴールです。

このように一気に複数の(大きなビットの)データを扱う方法として、qRAMというものがあります。
qRAMと通常のデータベースの違いを簡単に説明しておきます。

これまでグローバーで探索するときに対象となるデータベースでは、データは連続して配置されていました。
(例：$|1\rangle \sim |2^n\rangle$)
しかし、今扱いたい複数のデータはそれ自体が複数ビットから成るものであり、そのままグローバーで探索するのは大変です。
例えばデータが$|1\rangle \sim |2^n\rangle$の場合はHゲート一発で初期化ができますが、スパースなデータを初期化するのは少し面倒です。

そこで、それらのデータを連続するアドレスで管理しようというのがqRAMです。

今回の問題では、4枚の盤面が与えられます。
なので2ビットのアドレスを用いて
$|00\rangle \to $(1つ目の盤面)、$|01\rangle \to $(2つ目の盤面)...
というように設定して、このアドレスの重ね合わせから条件を満たすものをグローバーで探索すればよいです。

解答が少し込みいった実装になるため、前回の課題の解答を少しリファクタリングしておきましょう。

def week2a_ans_func(lights):
    num_iter = 17
    data = QuantumRegister(9)     # 盤面
    solution = QuantumRegister(9) # スイッチ
    ancilla = QuantumRegister(5)  # mct用の補助ビット
    oracle = QuantumRegister(1)   # オラクル
    c = ClassicalRegister(9)
    qc = QuantumCircuit(data, solution, ancilla, oracle, c)

    qc.x(oracle)
    qc.h(oracle)
    qc.h(solution)
    for i in range(9):
        if lights[i]:
            qc.x(data[i])    

    def switch_superpose():
        for i in range(3):
            for j in range(3):
                for (x,y) in [(-1,0), (0,-1), (0,0), (1,0), (0,1)]:
                    if i+x in range(3) and j+y in range(3):
                        qc.cx(solution[3*i + j], data[3*(i+x) + (j+y)])
    
    def diffusion(qbit):
        qc.h(qbit)
        qc.x(qbit)
        qc.h(qbit[0])
        qc.mct(qbit[1:],qbit[0],ancilla)
        qc.h(qbit[0])
        qc.x(qbit)
        qc.h(qbit)
        
    for _ in range(num_iter):
        switch_superpose()
        qc.x(data)
        qc.mct(data, oracle, ancilla)
        qc.x(data)
        switch_superpose()
        diffusion(solution)
    
    # Change the endian 
    qc = qc.reverse_bits() 
    qc.measure(solution,c)

    return qc

だいぶすっきりしました。
主な変更点は以下の通りです。

• 量子ビットを用途別に定義した
• オラクルの直前までを一つの関数にした
  • 自己逆なので、もとに戻す際も同じ関数でよい
• ライトが消えている判定(オラクルの最後)をxorのべた書きからx+mctに変更
• diffusionも関数にした

あと、テストコードもまた作りました。
とはいっても前回のものとほぼ同じです。

from qiskit import Aer

lightsout4=[[1, 1, 1, 0, 0, 0, 1, 0, 0],[1, 0, 1, 0, 0, 0, 1, 1, 0],[1, 0, 1, 1, 1, 1, 0, 0, 1],[1, 0, 0, 0, 0, 0, 1, 0, 0]]

# 他のパズルを試すときは引数lightsout4に指定する
def prepare_ex2b(func, lightsout4=lightsout4):
    backend = Aer.get_backend('qasm_simulator')
    qc = func(lightsout4)
    return execute(qc, backend=backend, shots=100, seed_simulator=12345, backend_options={"fusion_enable":True})

job  =  prepare_ex2b(week2b_ans_func)

result = job.result()
count = result.get_counts()
count = sorted(count.items(), key=lambda x:x[1], reverse=True)
print(count[0])
# 最も観測回数が多いビット列が解として扱われます。

解答

アドレスでグローバーをするだけ…
とはいえ、アドレスに対するオラクルを考えるのが少し難しいです。

難しいというか、この方針でいいのか？という感情を抱きながら実装しました。
(結果的にはそれで正しいようです)

以下その方法を説明します。

まずはナイーブに考えてみます。
例題の、「1回のスイッチで解ける場合」ならまだ簡単にできそうな感じがするんですよね。
「9個のスイッチをそれぞれ一つだけ押した場合にライトが消えたものがあればオラクルを返す」という感じに実装すればよいので。
しかし3個のスイッチを使うとなると、9C3通りでこれを考えることになるので微妙…

少し整理しましょう。
3つのスイッチで解ける、というオラクルを表現しようとすると、少なくとも各盤面の解にアクセスできる必要があるように思えます。

それはまさに前回の課題であり、私たちはグローバーを使って各盤面に対する解を見つけることができます。

その解のスイッチの個数が3個であることはどうやってわかるでしょうか？

これは、…

ここまで考えたとき、私は結構驚きました。
なんとweek 1-aの全加算器が使えます！

ナイーブに9ビットの和を表現してあげて、その結果が3であるときにオラクルが返ってくるような実装をしてあげればよい…！

というわけでオラクルの作り方が見えてきました。
少し戻って、問題は「(アドレスの)グローバーの中で(盤面の)グローバーなんてやって大丈夫なのか…？」という心配です。
高確率とはいえ決定的アルゴリズムじゃないので、多段にしたら精度が落ちるのでは…
もっと悪いのは、二重のグローバーなんて反復回数がバカみたいに多くなるんじゃないのか…

といろいろ不安になりました。

まぁしかし、そんなものはやってみてから考えればよいのです。

レッツ実装、実装。
(注：実際には結構めんどくさいと思って躊躇しました)

def week2b_ans_func(lightout4):
    
    num_bit = 2    
    inner_iter = 17
    outer_iter = 1
    
    address = QuantumRegister(num_bit)  # アドレス
    data = QuantumRegister(9)           # 盤面
    solution = QuantumRegister(9)       # どのスイッチを押すか
    ancilla = QuantumRegister(5)        # mct用の補助ビット
    counter = QuantumRegister(3)        # スイッチの個数を表す(全部で9つだが3ビットあれば十分であることに注意)
    oracle = QuantumRegister(2)         # oracle (今回は二つある)
    c = ClassicalRegister(num_bit)
    qc = QuantumCircuit(address, data, solution, counter, ancilla, oracle, c)
    
    # Initialization
    qc.h(address)
    qc.x(oracle)
    qc.h(oracle)
    qc.h(solution)
    
    def qram():
        '''
        address 00 -> board 0
        address 10 -> board 1 (bitの順番に注意, 観測するときには勝手に逆に戻る)
        address 01 -> board 2
        address 11 -> board 3
        '''
        for i in range(2**num_bit):
            for l in range(num_bit):
                if (i>>l)&1==0:
                    qc.x(address[l])
            for j in range(3):
                for k in range(3):
                    if lightout4[i][3*j + k]:
                        qc.ccx(address[0], address[1], data[3*j + k])
            for l in range(num_bit):
                if (i>>l)&1==0:
                    qc.x(address[l])
    
    def switch_superpose():
        for i in range(3):
            for j in range(3):
                for (x,y) in [(-1,0), (0,-1), (0,0), (1,0), (0,1)]:
                    if i+x in range(3) and j+y in range(3):
                        qc.cx(solution[3*i + j], data[3*(i+x) + (j+y)])
    
    def diffusion(qbit):
        qc.h(qbit)
        qc.x(qbit)
        qc.h(qbit[0])
        qc.mct(qbit[1:],qbit[0],ancilla)
        qc.h(qbit[0])
        qc.x(qbit)
        qc.h(qbit)
    
    def add(s):
        # qubit s をcounterに足す
        qc.mct([counter[1], counter[2], s], counter[0], ancilla)
        qc.ccx(counter[2], s, counter[1])
        qc.cx(s, counter[2])
    
    def add_rev(s):
        qc.cx(s, counter[2])
        qc.ccx(counter[2], s, counter[1])
        qc.mct([counter[1], counter[2], s], counter[0], ancilla)
    
    # Outer Grover
    for o_iter in range(outer_iter):
        qram()

        # Inner Grover
        for i_iter in range(inner_iter):
            switch_superpose()
            # 盤面のorをとってoracleの1ビット目に
            qc.x(data)
            qc.mct(data, oracle[0], ancilla)
            qc.x(data)
            switch_superpose()
            diffusion(solution)

        # solutionの全ビットの和をとる
        for i in range(9):
            add(solution[i])

        # counter=011 のとき oracle[1] を反転
        qc.x(counter[0])
        qc.mct(counter, oracle[1], ancilla)
        qc.x(counter[0])

        for i in range(9):
            add_rev(solution[i])

        # Reverse inner grover
        for i_iter in range(inner_iter):
            diffusion(solution)
            switch_superpose()
            qc.x(data)
            qc.mct(data, oracle[0], ancilla)
            qc.x(data)        
            switch_superpose()

        # qramへの書きこみを戻す
        qram()

        # diffusion
        diffusion(address)

    qc.measure(address, c)
    return qc

というわけで、グローバーの中に見事グローバーが入りました。
気を付けないといけないのは、「中のグローバー」も「qRAM」も外のグローバーのオラクルの補助ビットなので、オラクルを返した後にどちらももう一度逆に実行して元に戻します。

これでやってみたところ、少し実行に時間はかかりましたが100%の精度で求解することができました。
二段グローバーってできるものなんですね。

めでたしめでたし…

##9. Week 3: 最終問題

と個人的にエンディングムードが漂っていた中、ラスボス登場。

…

…

むずすぎます。

問題の内容はWeek 3のページをご覧ください。

いかにも今までのテクニック(多段グローバー。qRAM)を駆使して解けそうな課題ですが…
問題はビット数です。

前回までのように、オラクルを作るためにレーザーと盤面をすべてビットで表現すると、それだけで28ビットを越えてしまいます。

(アドレス 4 bit + ノイズクラスタ 16 bit + レーザー 8 bit = 28 bit にオラクルや補助ビットを加えた場合)

う～ん、どうしよう…

とりあえずテストコードはいつも通り作っておきましょう。
(実はこの問題については、ろくに実装することもままならなかったため、このテストコードはほぼ使われなかったのでした…でも作り方は前回までと完全に同じ)

problem_set = \
    [[['0', '2'], ['1', '0'], ['1', '2'], ['1', '3'], ['2', '0'], ['3', '3']],
    [['0', '0'], ['0', '1'], ['1', '2'], ['2', '2'], ['3', '0'], ['3', '3']],
    [['0', '0'], ['1', '1'], ['1', '3'], ['2', '0'], ['3', '2'], ['3', '3']],
    [['0', '0'], ['0', '1'], ['1', '1'], ['1', '3'], ['3', '2'], ['3', '3']],
    [['0', '2'], ['1', '0'], ['1', '3'], ['2', '0'], ['3', '2'], ['3', '3']],
    [['1', '1'], ['1', '2'], ['2', '0'], ['2', '1'], ['3', '1'], ['3', '3']],
    [['0', '2'], ['0', '3'], ['1', '2'], ['2', '0'], ['2', '1'], ['3', '3']],
    [['0', '0'], ['0', '3'], ['1', '2'], ['2', '2'], ['2', '3'], ['3', '0']],
    [['0', '3'], ['1', '1'], ['1', '2'], ['2', '0'], ['2', '1'], ['3', '3']],
    [['0', '0'], ['0', '1'], ['1', '3'], ['2', '1'], ['2', '3'], ['3', '0']],
    [['0', '1'], ['0', '3'], ['1', '2'], ['1', '3'], ['2', '0'], ['3', '2']],
    [['0', '0'], ['1', '3'], ['2', '0'], ['2', '1'], ['2', '3'], ['3', '1']],
    [['0', '1'], ['0', '2'], ['1', '0'], ['1', '2'], ['2', '2'], ['2', '3']],
    [['0', '3'], ['1', '0'], ['1', '3'], ['2', '1'], ['2', '2'], ['3', '0']],
    [['0', '2'], ['0', '3'], ['1', '2'], ['2', '3'], ['3', '0'], ['3', '1']],
    [['0', '1'], ['1', '0'], ['1', '2'], ['2', '2'], ['3', '0'], ['3', '1']]]

# 他のパズルを試すときは引数problem_setに指定する
def prepare_ex3(func, problem_set=problem_set):
    backend = Aer.get_backend('qasm_simulator')
    qc = func(problem_set)
    return execute(qc, backend=backend, shots=100, seed_simulator=12345, backend_options={"fusion_enable":True})

job = prepare_ex3(week3_ans_func)

result = job.result()
count = result.get_counts()
count = sorted(count.items(), key=lambda x:x[1], reverse=True)
print(count[0])
# 最も観測回数が多いビット列が解として扱われます。

さて、解き方についてですが、
なんとか少ないビットで表現する方法をいろいろ考えて、面白いアイデアをいくつか出しました。

• ノイズクラスタの座標を縦横2bitずつで表現して、重ね合わせで複数個を表す
  • ナイーブにノイズクラスタを持つと16ビットのところを4ビットに削減する
  • レーザがノイズクラスタに当たる判定はもう一段グローバーをかませることで原理的には実現できる
  • しかし「解けない盤面」を見つけるのには微妙に向いていなくて、実装はしてみたものの撃沈
• 「3回のレーザーで消えない場所」を少ないビット数で表現する(残りのマスは1×4か2×3の長方形になる)
  • これはどうやって実装したらいいかよくわからなかったのでボツ
• 「解けない盤面」を直接表すために、1～4 vs 1～4のすべての組み合わせのマス目を含むようなノイズクラスタの配置を探す
  • これも具体的な表現の仕方がわからずボツ…
  • (解説を読んで知りましたが、実はこのアイデアは非常によくかすっていたのでした…あまりヒントにならないように上はあえてわかりにくい日本語で書いています)

という感じで、考えつつ手を動かしつつ、むなしく時は流れ…

結局ギブアップし、一緒に取り組んでいた友人と一緒に解説を読みました。

解答

この問題については考え方も実装も丁寧に解説されている公式解答ページを見るのが良いと思います。

ちなみに、演習問題と一緒に置いてあったヒントのページの存在を後で知りました。
ヒントに頼らずとも、この手の問題が二部グラフの被覆問題に落とせるというのは界隈では常識とのうわさも聞きました…
最終問題までほとんどアルゴリズムの工夫の話が出てきてなかったので虚を突かれた感じがしましたが、まぁ競プロみたいな問題は普段からちゃんと触れておこうねということで…

というわけで最終問題は簡素ですがこれくらいで終わりにします！

#-1. おわりに

今回は、IBM Quantum Challenge 2020 に過去問チャレンジしてみました！
難易度もちょうどよく、非常に楽しめた数週間でした。

Qiskitに初めて触れてみるという目的で取り組んでみましたが、これは他の方にも強くお勧めできる教材と言えると思います！

全体を通して、量子/古典ともにアルゴリズムの知識が少しあるとより学習効果が高そうだなと感じました。
もちろん全く知識がなくても、サンプルコードを触ったり前半の問題を解くことで量子プログラミングに親しむきっかけに十分なると思います。

それでは、今回はこのへんで！

1. 実際、私が他数人と上述のQuantum Native Dojoと書籍「量子コンピュータによる機械学習」を読む勉強会をして得られた「理屈はわかったような気はするけど何もわかってない気もする」という満場一致の感想が、本記事のチャレンジのきっかけになったのでした ↩

2. 所望のユニタリ変換自体は$|c\rangle$なしで定義できますし、普通は書かずに説明されると思います。しかし実装する上でも$|c\rangle$を明示した方が理解しやすいためここでは付けた形で書きました。 ↩

3. なお、本記事およびコンペの目的として実装に触れるために実際の実行を通して最適な反復回数を求めましたが、解析的に $\pi \sqrt N /4$ (に最も近い整数)回の反復が最適であることが知られています。 ↩

4. 私は大昔にYahooのグリーティングカードで「花粉症になったモアイ像を助けるために花粉をつぶすゲーム」としてよくやっていたのでした。作者のページを見つけましたがグリーティングカードサービスは5年ほど前に終わってしまっていたようです…面白かったのに残念… ↩

5. 行っていることは等価ですが、回路のコスト(Week 1-a参照)としてはxorの方が2~3倍小さくできるようです。一方で回路を実行するまで(=回路を生成する？)時間が少なくとも私の環境ではかなり長くなってしまう(~数分)のでいいのか悪いのかよくわからない… ↩