chainerの作法 その２

概要

chainerの作法、調べてみた。
回帰。

インポート

import numpy as np
import matplotlib.pyplot as plt
import chainer
from chainer import Function, gradient_check, Variable, optimizers, serializers, utils
from chainer import Link, Chain, ChainList
import chainer.functions as F
import chainer.links as L

訓練データセットのイテレーション

-3.0から+3.0の100点
sinが教師データ
dataset、iteratorは、使わん。

	X = np.linspace(-3.0, 3.0, num = 100, dtype = np.float32)
	T = np.sin(X)

ミニバッチに対する前処理

エポックは、300
ミニバッチは、100

	n_epoch = 300
	n_batch = 100

ニューラルネットワークのForward/backward計算

回帰なので、活性化関数は、tanh
lossは、mean_squared

class MLP(Chain):
	def __init__(self):
		super(MLP, self).__init__(l1 = L.Linear(1, 20), l2 = L.Linear(20, 1), )
	def __call__(self, x):
		h = F.tanh(self.l1(x))
		out = self.l2(h)
		return out

class M_fit(Chain):
	def __init__(self, predictor):
		super(M_fit, self).__init__(predictor = predictor)
	def __call__(self, x, t):
		y = self.predictor(x)
		loss = F.mean_squared_error(y, t) * 0.5
		return loss
	def predict(self, x):
		y = self.predictor(x)
		return y

パラメータの更新

オプチマイザーは、Adam

optimizer = optimizers.Adam()
	optimizer.setup(model)

評価データセットにおける現在のパラメータの評価

Variableに、データを流し込む。

	for epoch in range(n_epoch):
		indexes = np.random.permutation(np.size(X))
		for i in range(n_batch):
			model.zerograds()
			x = Variable(np.array([[X[indexes[i]]]], dtype = np.float32))
			t = Variable(np.array([[T[indexes[i]]]], dtype = np.float32))
			loss = model(x, t)
			loss.backward()
			optimizer.update()

中間結果をログに残す

エポックとloss。

		print ('epoch : ', epoch, 'loss : ', loss.data)

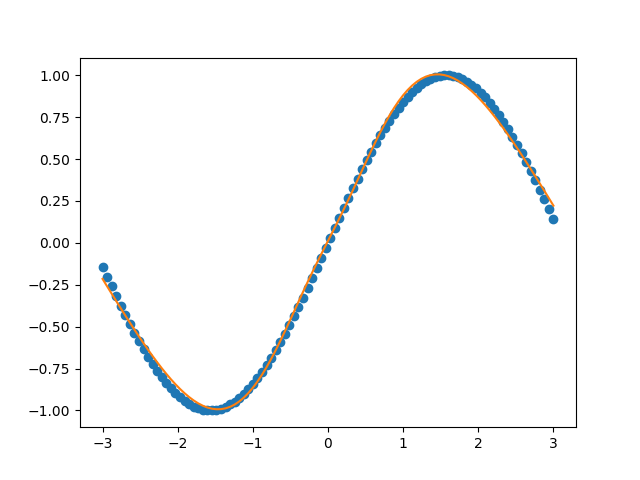
結果

いい感じ。

以上。