これはなに
社内の勉強会で発表するときに使った資料です
1.3 ニューラルネットワークの学習
1.3.1 損失関数
ニューラルネットワークで"良い推論"をするためには、最適なパラメータを設定しなければならない
ニューラルネットワークの学習には、学習がどれだけ上手くいっているかを知るための指標が必要
→損失という
ニューラルネットワークの損失を求めるために使うのが損失関数
- 損失関数
- 2乗誤差(ゼロから始めるDeep Learning 1 にあった)
- @ohakutsu 回帰に使うのかな?
- 交差エントロピー誤差
- 多クラス分類に用いられることが多い
- 2乗誤差(ゼロから始めるDeep Learning 1 にあった)
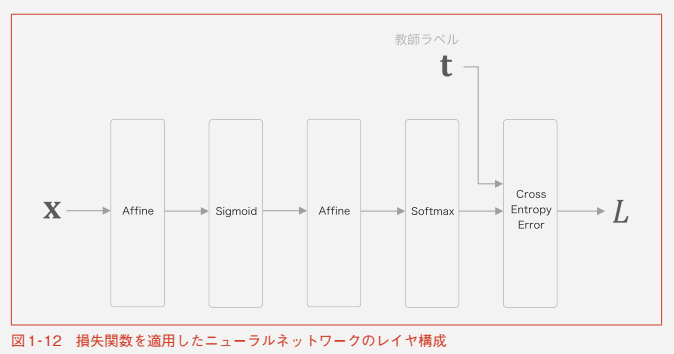
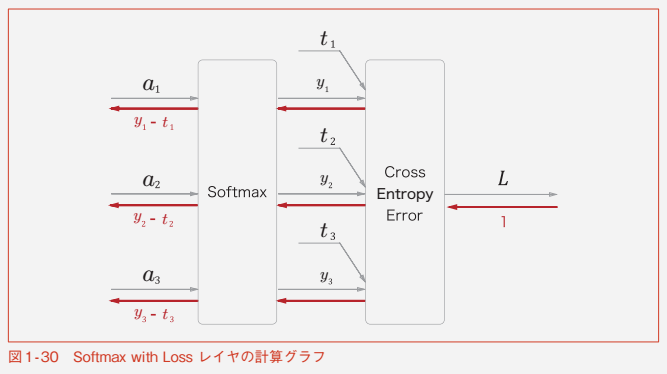
今節では、損失を求めるのに以下のようなレイヤ構成にする
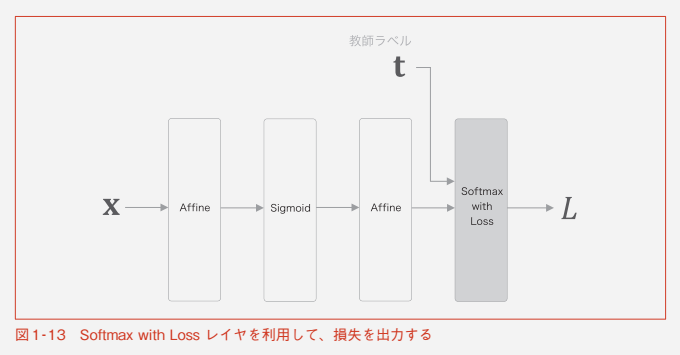
Softmax と Cross Entropy Error のレイヤをまとめて、
Softmax with Loss とする
Softmaxとはなんぞや
→ソフトマックス関数
y_k = \frac {exp(s_k)}{\displaystyle \sum _{i=1}^{n} exp(s_i)}
- 特徴
- 出力が0.0〜1.0の実数
- 出力をすべて足すと1.0になる
- 確率として解釈することができる
Cross Entropy Errorとはなんぞや
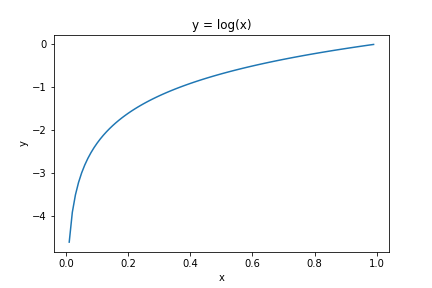
→交差エントロピー誤差
L = - \sum_{k}t_k\space log\space y_k
- 特徴
- t は
one_hot表現(0か1)の教師ラベルなので、ラベルが1のときの自然対数を返すだけ - yが0に近いほど小さくなり、1に近いほど0に収束する
- t は
ミニバッチ処理を考慮して、
L = - \frac{1}{N} \sum_{n}\sum_{k}t_{nk}\space log\space y_{nk}
を使う
1.3.2 微分と勾配
ニューラルネットワークの学習の目標は、損失をできるだけ小さくするパラメータを見つけること
ここで重要になるのが微分、勾配である
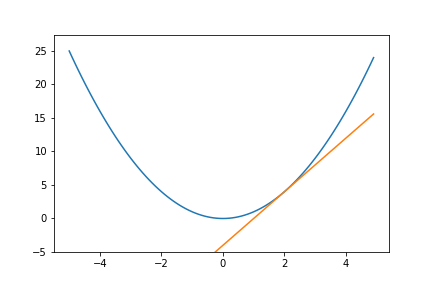
微分
→ある瞬間の変化の量
@ohakutsu 中学数学からはじめるAI(人工知能)のための数学入門 - YouTube でわかります
y = f(x)
の x に関する y の微分は
\frac{dy}{dx}
と表せる
変数が複数あっても微分を求めることができる
x をベクトルとして、
L = f(x)
\frac{\partial L}{\partial x} = \left( \frac{\partial L}{\partial x_1}, \frac{\partial L}{\partial x_2}, ..., \frac{\partial L}{\partial x_n} \right)
ベクトルの各要素の微分をまとめたものを勾配と呼ぶ
行列の場合も同様に勾配を考えることができる
W を m×n 行列として、
L = g(W)
\frac{\partial L}{\partial W} = \left(
\begin{array}{ccc}
\frac{\partial L}{\partial w_{11}} & \cdots & \frac{\partial L}{\partial w_{1n}} \\
\vdots & \ddots & \\
\frac{\partial L}{\partial w_{m1}} & & \frac{\partial L}{\partial w_{mn}}
\end{array}
\right)
1.3.3 チェインルール
学習時におけるニューラルネットワークは、学習データを与えると損失を出力する
各パラメータに関する損失の勾配が得られると、それを使ってパラメータの更新をすることができる
ニューラルネットワークの勾配をどのように求めるか
→誤差逆伝播法
誤差逆伝播法を理解する上でキーとなるのがチェインルール(連鎖律)
- チェインルール
- 合成関数に関する微分の法則
↓こんなやつ
y = f(x) \\
z = g(y) \\
書き換えて
z = g(f(x)) \\
x に関する z の微分は
\frac{\partial z}{\partial x} = \frac{\partial z}{\partial y}\frac{\partial y}{\partial x}
どれだけ複雑な関数を扱うとしても、その微分は個別の関数の微分で求めることができる
1.3.4 計算グラフ
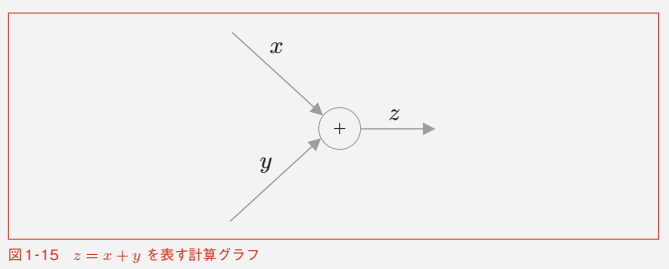
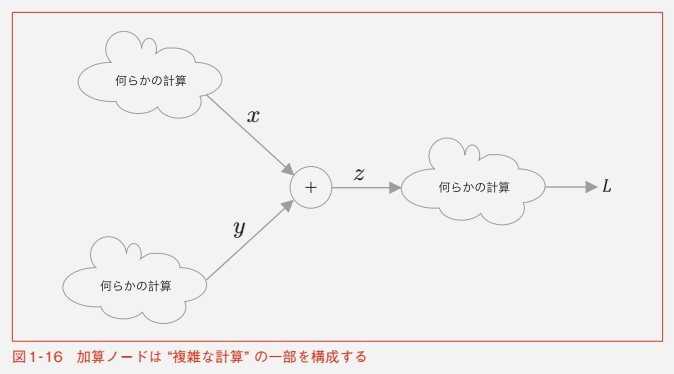
計算を視覚的に表すもの
例)
z = x + y
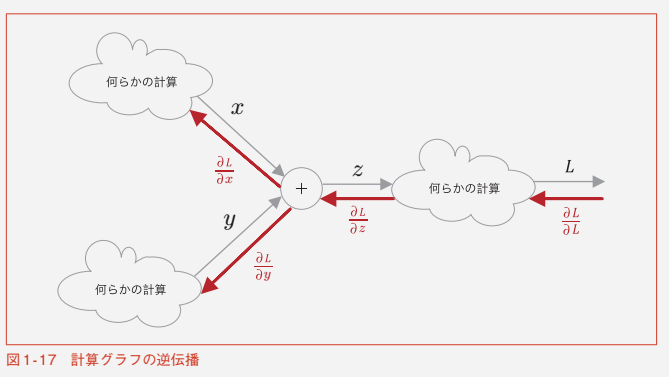
逆方向の伝搬が「逆伝搬」
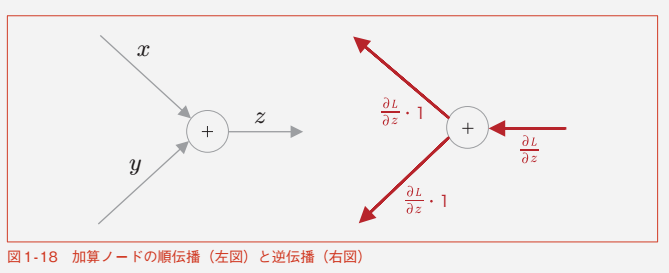
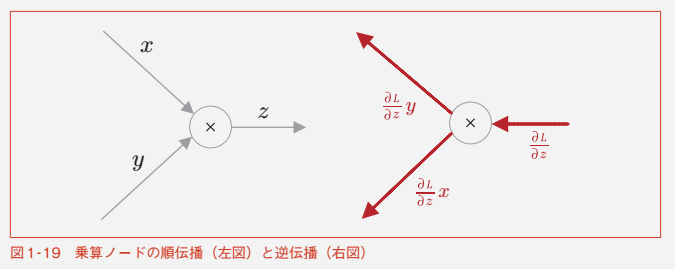
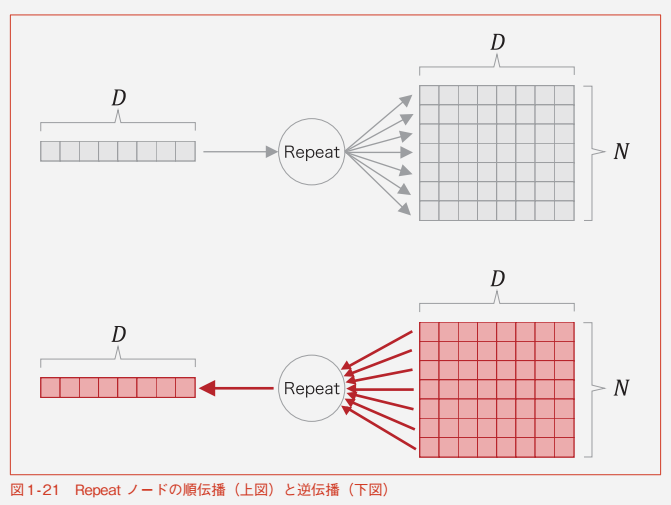
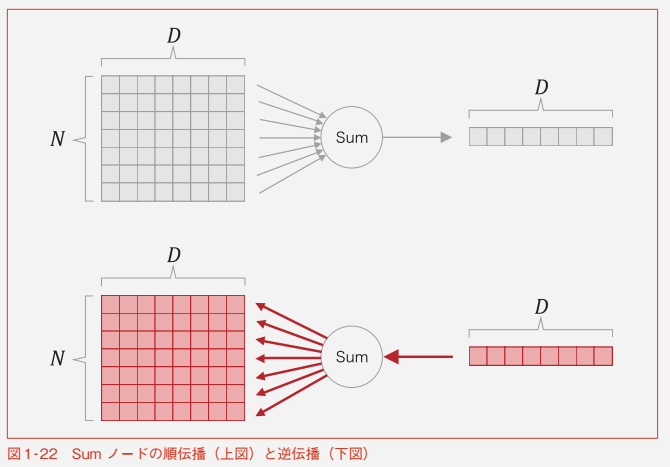
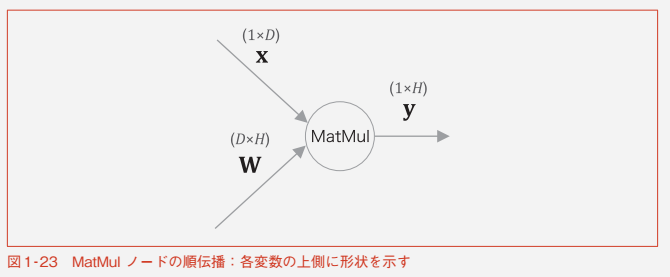
以下、代表的な演算ノード
1.3.5 勾配の導出と逆伝搬の実装
各レイヤを実装していく
Sigmoidレイヤ
シグモイド関数は
y = \frac {1}{1 + exp(-x)}
シグモイド関数の微分は
\frac{\partial y}{\partial x} = y(1 - y)
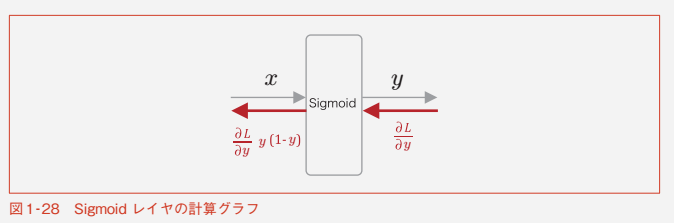
Sigmoidレイヤの計算グラフは
Pythonで実装すると
class Sigmoid:
def __init__(self):
self.params, self.grads = [], []
self.out = None
def forward(self, x):
out = 1 / (1 + np.exp(-x))
self.out = out
return out
def backward(self, dout):
dx = dout * (1.0 - self.out) * self.out
return dx
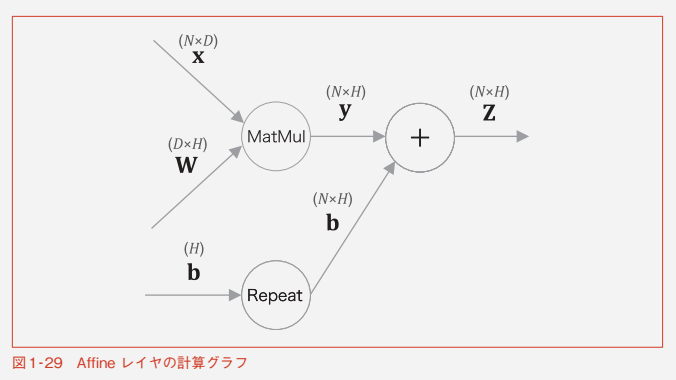
Affineレイヤ
Affineレイヤの順伝搬は
y = np.dot(x, W) + b
バイアスの加算がブロードキャストされている
Pythonで実装すると
class Affine:
def __init__(self, W, b):
self.params = [W, b]
self.grads = [np.zeros_like(W), np.zeros_like(b)]
self.x = None
def forward(self, x):
W, b = self.params
out = np.dot(x, W) + b
self.x = x
return out
def backward(self, dout):
W, b = self.params
dx = np.dot(dout, W.T)
dW = np.dot(self.x.T, dout)
db = np.sum(dout, axis=0)
self.grads[0][...] = dW
self.grads[1][...] = db
return dx
Softmax with Lossレイヤ
class SoftmaxWithLoss:
def __init__(self):
self.params, self.grads = [], []
self.y = None # softmaxの出力
self.t = None # 教師ラベル
def forward(self, x, t):
self.t = t
self.y = softmax(x)
# 教師ラベルがone-hotベクトルの場合、正解のインデックスに変換
if self.t.size == self.y.size:
self.t = self.t.argmax(axis=1)
loss = cross_entropy_error(self.y, self.t)
return loss
def backward(self, dout=1):
batch_size = self.t.shape[0]
dx = self.y.copy()
dx[np.arange(batch_size), self.t] -= 1
dx *= dout
dx = dx / batch_size
return dx
1.3.6 重みの更新
誤差逆伝播法によって求めた勾配を使ってニューラルネットワークのパラメータを更新する
ニューラルネットワークの学習は以下の手順で行う
- ミニバッチ
- データが多いと、時間がかかってしまうため、データの一部を全体の近似として使う(ゼロから始めるDeep Learning 1 より)
- 勾配の算出
- 誤差逆伝播法で、各重みパラメータに関する損失関数の勾配を求める
- パラメータの更新
- 1~3を繰り返す
3. パラメータの更新
2. 勾配の算出で求めた勾配を使い、パラメータを勾配の逆方向(損失を減らす方向)に更新をする
→勾配降下法
ここでは、重みの更新方法で最も単純なSGDを使う(他にも何種類かゼロから始めるDeep Learning 1に書いてた)
W \leftarrow W - \eta \frac{\partial L}{\partial W} \\
\eta : 学習係数
Pythonで実装すると
class SGD:
def __init__(self, lr=0.01):
self.lr = lr
def update(self, params, grads):
for i in range(len(params)):
params[i] -= self.lr * grads[i]
実際のニューラルネットワークのパラメータの更新は以下のようになる
model = TwoLayerNet( ... )
optimizer = SGD()
for i in range(10000):
...
x_batch, t_batch = get_mini_batch( ... ) # ミニバッチの取得
loss = model.forward(x_batch, t_batch)
model.backward()
optimizer.update(model.params, model.grads)
...
1.4で実際にニューラルネットワークの学習を行う