LoginSignup
0
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 3 years have passed since last update.

@ohagikureta(れあ く)

1day 実装 深層学習レポート　ラビット☆チャレンジ 提出レポート

Posted at

1day 実装 深層学習レポート

識別モデル・生成モデル

  • 識別モデル
    - 識別モデルには、決定着、ロジスティック回帰分析、サポートベクターマシンなどがある
    - 特徴として、高次元から低次元に変換したり、必要な学習データが少量で済む
    - 画像認識によく使われる
    - 例：犬の画像の判別など
    - 生成モデル
    - 生成モデルには、隠れマルコフモデル、ベイジアンネットワーク、変分オートエンコーダなどがある
    - 特徴として、低次元から高次元に変換したり、必要なデータは大量に必要である
    - 例：画像の解像度の工場や、テキスト生成

Section1: 入力層～中間層

  • 入力に対して、ニューラルネットワークでは重み（ウェイト）という値を分け与える
    • 重みがかけ合わさった値が中間層に入力されノードが生成される
    • 重みだけでは、値の調整ができないため、バイアスを書けることによって適切な結果をアウトプットすることができる
    • 上記ででた中間層に入力された値をμと記載する
    • μは活性化関数を用いて算出する

Section2: 活性化関数

  • モデルの表現力を増すために活性化関数を用いる
  • 具体的な活性化関数とは
    • 中間層に用いられる活性化関数
      • シグモイド関数、ステップ関数、ソフトマックス関数
        • ステップ関数：歴史的に用いられてきた活性化関数
          • シグモイド関数に比べ直角なグラフで表される
    • 非線形な活性化関数
      • なだらかなグラフの出力ができる
        • O-1の数値で出力がかのう、微分が使えるため複雑なけいさんから、幅広い学習ができるようになった
    • シグモイド関数の活用により勾配消失問題が発生（絶対値が大きくなると、勾配が小さくなってしまう）
      • RELU関数である程度解消できる
    • 活性化関数を使うことにより、有効な説明変数を見つけることができる（特徴量）

Section3: 出力層

  • 出力層の役割
    • NNを学習させるために必要なデータ：訓練データ
    • 入力データと訓練データ（正解値）を用意する必要がある
    • NNのフローは下記の通りとなり、出力値と正解値の差（答え合わせ）を行う
      • ①入力データをNNに居れる
      • ②説明変数から判別の確率を出力する
      • ③訓練データとの評価を行う
    • ③の結果と正解値との差を誤差関数で出力する
      • 答えがどれくらい間違っているか？を式で表す
        • 二乗和誤差：12∑(yi−di)2
    • 二乗和誤差のコード
      • functions.mean_squared_error(d, y)
    • 出力層の活性化関数
      • 中間層と出力数で活性化関数を利用する目的が異なる。
      • 中間層で学習されたデータを、人間が使いやすいように加工してくれる関数を用いる
        • 中間層で出さた信号の大きさの比率をそのままに変換する
        • 確率で抽出するために0~1の範囲に指定し、全体を１とするように確率で会わらせるようにする
    • 出力層の活性化関数は自分で解きたい問題に合わせて使い分けできる
      • 回帰の場合：恒等写像関数 y=x / 誤差関数は二乗誤差※ 平均二乗和誤差を使う事のが多い（クロスエントロピー）
      • 分類の問題： シグモイド関数 y=11+exp−x / 誤差関数は交差エントロピー（クロスエントロピー）
      • タクラス分類：ソフトマックス関数 y(i,u)=eui∑Kk=1euk / 誤差関数は交差エントロピー（クロスエントロピー）
        • 犬猫を見分けるとか
    • シグモイド関数コード
      • def sigmoid(x):return 1/(1 + np.exp(-x))
    • ソフトマックス関数コード
      • すべてのクラスを足し合わせると1になる（確率を出せる）
      • def softmax(x):if x.ndim == 2:x = x.Tx = x -np.max(x, axis=0)y = np.exp(x) /np.sum(np.exp(x), axis=0)return y.Tx = x -np.max(x) # オーバーフロー対策return np.exp(x) / np.sum(np.exp(x))
    • 平均二乗誤差のコード
      • def mean_squared_error(d, y):return np.mean(np.square(d - y)) / 2数式S3_2) 出力層_活性化関数Python数式とコード日本語
    • 交差エントロピー（何でも使う）

Section4: 勾配降下法

  • 勾配降下法とは、NNを学習させるための手法
    • 学習を問うして誤差を最小にするネットワークを作成すること
    • 前回の学習で間違えた結果を活かすための手法
      • 誤差が減るように重みを加える
    • 学習率が高くなると最小値にいつまでもたどり着かず発散してしまう現象がおきる
    • 学習率が小さすぎても最適な解にたどり着くまでに時間がかかる
  • 勾配降下法のアルゴリズム論文
    • Adam
  • 学習ステップ
    • 誤差関数から次の学習の重みを反映更新を行う。この一回のサイクルをエポックと呼ぶ
  • 確率的勾配降下法
    • 別名SGDと呼ぶ
    • 学習に使う全データから一部ランダムに画像を選び学習を進める手法
    • 毎回異なるデータを使うため、局所極小解に収束するリスクの軽減
    • オンライン学習ができる
      • オンライン学習はモデルに都度都度データを与えて学習ができる
        • POSデータとか天候データとかに使える
  • ミニバッチ勾配降下法
    • ランダムに分割したデータの集合に属するサンプルの平均誤差
      • 例をあげると10万枚の画像を200枚ごとに小分けにして機械学習する。小分けのことをミニバッチという
      • 一般的に使われる手法
      • 一つの命令を同時並行して学習することができる
  • 誤差勾配の計算
    • 疑似的に微分を計算する手法
    • 順伝播の計算を繰り返し行うため負荷が大きい

sesstion5 誤差逆伝播法

  • 算出された誤差を、出力層側から順に微分し、前の層前の層へと伝播。
  • 最小限の計算で各パラメータでの微分値を解析的に計算する手法
  • 誤差から微分を逆算することで、不要な再帰的計算を咲けて微分を算出できる

確認テストの考察

  • 【P11】ディープラーニングは、結局何をやろうとしているか2行以内で述べよ。

  • また、次の中のどの値の最適化が最終目的か。 全て選べ。

  • ①入力値[ X] ②出力値[ Y] ③重み[W]④バイアス[b] ⑤総入力[u] ⑥中間層入力[ z] ⑦学習率[ρ]

    • 考察
      • ③の重み④のバイアスだと考えられる。ニューラルネットワークは多数の中間層を持っており、出力値に達するまでに、各出力値に対する確率を出すために、重みやバイアスを掛けて調整し最適化する必要があると考えられる。

  • 【P13】次のネットワークを紙にかけ。

    • 入力層：2ノード1層
    • 中間層：３ノード2層
    • 出力層：1ノード1層
    • 考察
      • 下記写真

  • 【P20】この図式に動物分類の実例を入れてみよう。

    • 考察
      • 動物の例を入れる
        • x1:身体の面積
        • x2:足の本数
        • x3:毛の長さ
        • x4:歯の本数
        • b:バイアス

  • 【P22】この数式をPythonで書け。

    • 考察

      • u1 = np.dot(x, W1) + b1S1)

      • np.dot(x, W1)...行列式を表す

      • 順伝播単層単ユニット

      • 下記コードでも同様の処理を行っている
        W = np.array([1,2,3,4])
        x = np.array([4,3,2,1])
        b = 10
        print (compute_u(W,x,b))
        30

  • 【P24】1-1のファイルから 中間層の出力を定義しているソースを抜き出せ。

    • 考察
      • 中間層出力
        z = functions.relu(u)
        print_vec("中間層出力", z)
      • 中間層の出力と記載があったっため選択したが間違っていた
      • 回答

        • 2層の総出力

        • z2 = functions.relu(u2)

        • 出力層の総入力

        • u3 = np.dot(z2, W3) + b3

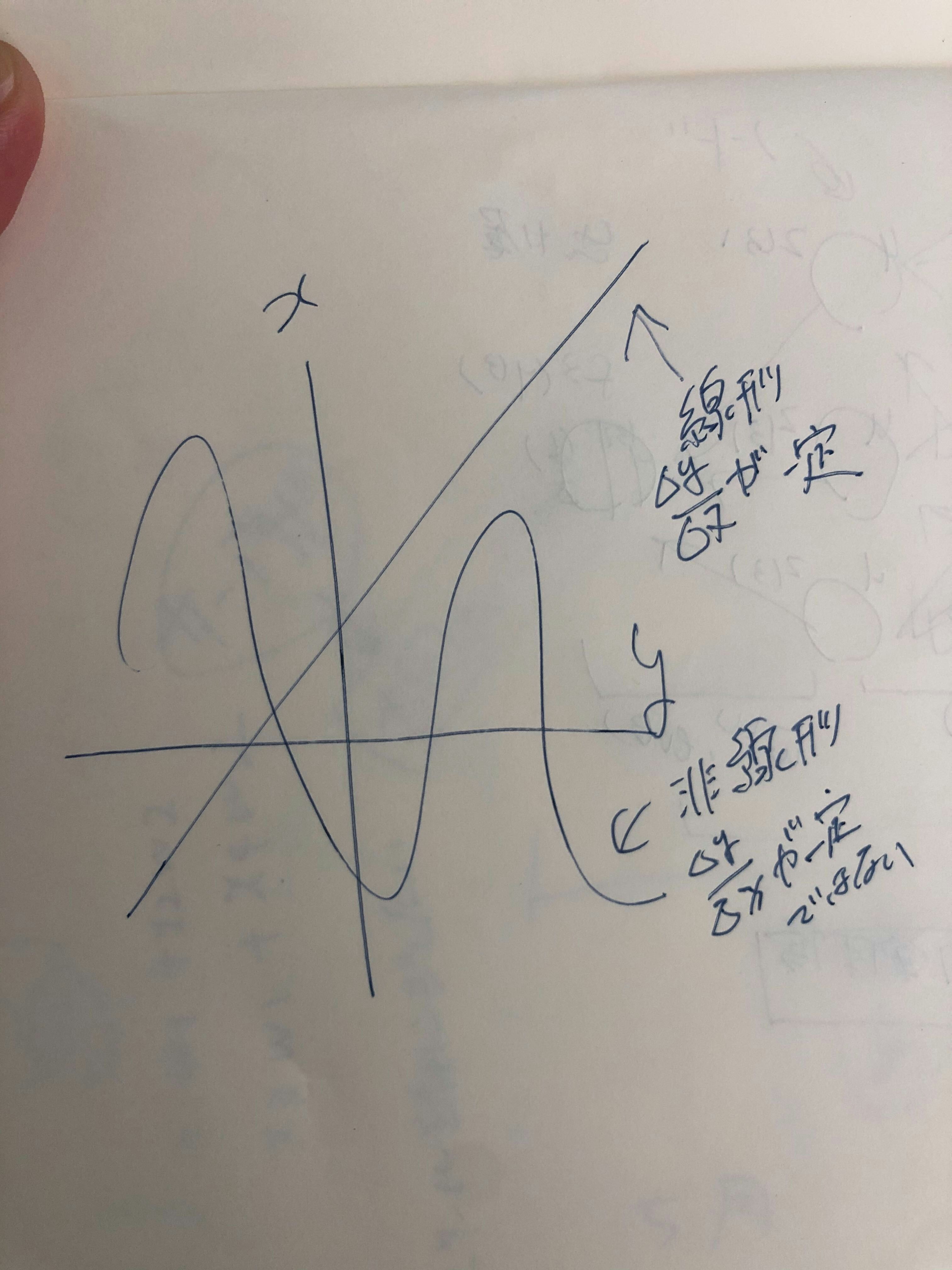
  • 【P27】線形と非線形の違いを図にかいて簡易に説明せよ。

    • 考察
      • グラフが直線形になる関数が線形関数で、そうでない関数が非線形関数となる
        -線形な関数の例 加法性
      • f(x)=x2xAx
      • 非線形な関数の例
      • f(x)=x2,sinx,ex,logx
      • 写真を添付

  • 【P34】配布されたソースコードより該当する箇所を抜き出せ。

    • 考察(活性化関数を表すコード)
      # 1層の総出力 z1 = functions.relu(u1)
      - relu関数をよびだしているため

  • 【P45】

    • なぜ、引き算でなく二乗するか述べよ
    • 下式の1/2はどういう意味を持つか述べよ
      • 考察
        • なぜ、引き算でなく二乗するか述べよ
          • 誤差を引き算して足し算をすると0になってしまう
          • すべての値を正の値にする
        • 下式の1/2はどういう意味を持つか述べよ
          • 微分を実施するため

  • 【P52】①~③の数式に該当するソースコードを示し、一行づつ処理の説明をせよ。

  • 考察

ソフトマックス関数
    def softmax(x)://f(u) をリストとして返す関数
         if x.ndim == 2:・//プログラムを安定させるための一行
           x = x.T
          x = x - np.max(x, axis=0)
          y = np.exp(x) / np.sum(np.exp(x), axis=0)//exp 関数のすべての要素のに関して、 exp を底として指数の合計
              return y.T
        x = x - np.max(x) オーバーフロー対策
         return np.exp(x) / np.sum(np.exp(x))//exp 関数のすべての要素のに関して、 exp を底として指数の合計
    - softmaxを取って
    - minibatchとしてデータを取りあつかうために、同じことを二回羅列している
  • 【P53】①~②の数式に該当するソースコードを示し、一行づつ処理の説明をせよ。
    考察

クロスエントロピー
def cross_entropy_error(d, y): //平均二乗和誤差を定義
if y.ndim == 1://次元の配列を変更
d = d.reshape(1, d.size)//行列の中身のデータを変更せずに、行列の形状を変更
y = y.reshape(1, y.size)
教師データがone-hot-vectorの場合、正解ラベルのインデックスに変換
if d.size == y.size:
d = d.argmax(axis=1)//関数がその最大値をとる定義域
batch_size = y.shape[0]
※return -np.sum(np.log(y[np.arange(batch_size), d] + 1e-7)) / batch_size
- logの計算をnnp.sumで足し合わせて、いる
- 1e-7 をプラスしているのは対数関数が0に落ちないような処理をしている
- y,d は正規化されている0,1

  • 【P56】勾配降下法に該当するソースコードを探してみよう。
  • 考察
delta1 = delta1[np.newaxis, :]
b1の勾配
grad['b1'] = np.sum(delta1, axis=0)
x = x[np.newaxis, :]
W1の勾配
grad['W1'] = np.dot(x.T, delta1)
network[key]  -= learning_rate * grad[key]
- 回答
network[key]  -= learning_rate* grad[key]
grad = backward(x, d, z1, y)

  • 【P66】オンライン学習とは何か2行でまとめよ

    • 考察
    • ログデータやPOSデータなどのリアルタイムで取得されるデータに対して、そのデータを用いて確率的勾配降下法を行い、
      　随時重みとバイアスをパラメータを更新できる
    • 一方バッチ学習はすべてのデータを使って学習する手法

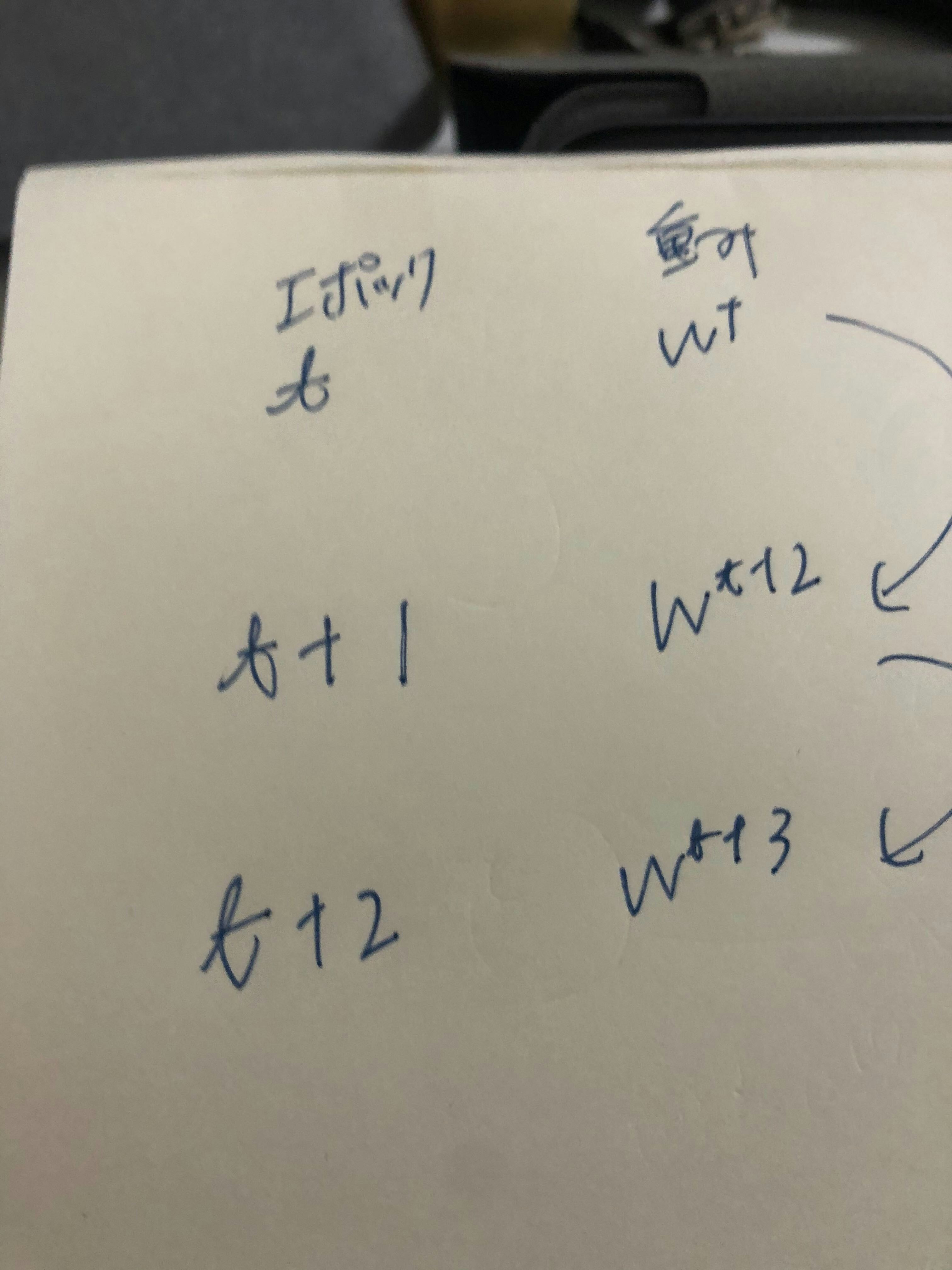
  • 【P69】ミニバッチ勾配降下法の数式の意味を図に書いて説明せよ。

    • 考察
    • 写真添付
  • 【P79】誤差逆伝播法では不要な再帰的処理を避ける事が出来る。 既に行った計算結果を保持しているソースコードを抽出せよ。
-  考察
- デルタがポイントとなる

functions.d_mean_squared_error：誤差関数を微分したもの
誤差逆伝播
def backward(x, d, z1, y):
print("\n##### 誤差逆伝播開始 #####")    

grad = {}

W1, W2 = network['W1'], network['W2']
b1, b2 = network['b1'], network['b2']

出力層でのデルタ
delta2 = functions.d_mean_squared_error(d, y)
b2の勾配
grad['b2'] = np.sum(delta2, axis=0)
W2の勾配
grad['W2'] = np.dot(z1.T, delta2)
中間層でのデルタ
delta1 = np.dot(delta2, W2.T) * functions.d_relu(z1)
delta1 = np.dot(delta2, W2.T) * functions.d_sigmoid(z1)

delta1 = delta1[np.newaxis, :]
 b1の勾配
grad['b1'] = np.sum(delta1, axis=0)
x = x[np.newaxis, :]
 W1の勾配
grad['W1'] = np.dot(x.T, delta1)

 print_vec("偏微分_重み1", grad["W1"])
 print_vec("偏微分_重み2", grad["W2"])
 print_vec("偏微分_バイアス1", grad["b1"])
 print_vec("偏微分_バイアス2", grad["b2"])|
return grad
  • 【P84】2つの空欄に該当するソースコードを探せ
    • 考察
    • ∂E∂y∂y∂u
    • b2の勾配
    • delta2 = functions.d_mean_squared_error(d, y)
    • ∂E∂y∂y∂u∂u∂w(2)ji
    • W2の勾配
    • grad['W2'] = np.dot(z1.T, delta2)
0
0
1

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
0
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?