『ベイズ推論による機械学習入門』Pythonのnumpyだけで実装するポアソン混合モデルの近似推論

先月読破した『ベイズ推論による機械学習入門』をPythonで実装してみました。

内容は、Chapter 4 の「4.3 ポアソン混合モデルにおける推論」です。

お花柄の緑本。これで入門って…機械学習深すぎ。笑

データの作成

今回は多峰性の１次元データとして、二峰性ポアソン分布を作成していきます。

import numpy as np
from matplotlib import pyplot as plt
%matplotlib inline

plt.figure(figsize=(12, 5))
plt.title('Poisson distribution', fontsize=20)

# サンプルデータの作成
Lambda_x1 = 30
Lambda_x2 = 50
samples_x1 = 300
samples_x2 = 200
x1 = np.random.poisson(Lambda_x1, samples_x1)
x2 = np.random.poisson(Lambda_x2, samples_x2)

# データの結合
X = np.concatenate([x1, x2])

plt.hist(X, 30, density=True, label='all data')
plt.legend()
plt.show()

結果は以下のようになります。
※ ポアソン分布のランダム性からグラフの形状が若干変化すると思います。

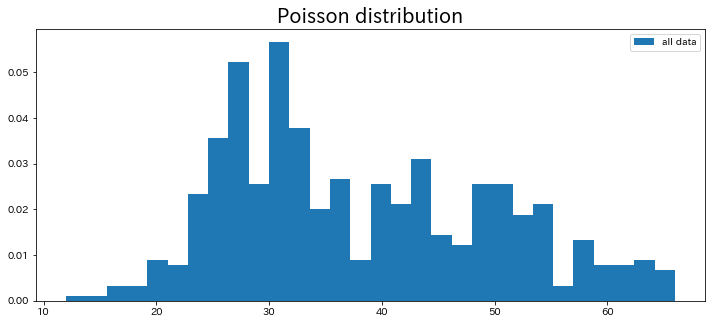
軽く解説すると、
平均値: 30, データ数: 300
平均値: 50, データ数: 200
の２つのポアソン分布が混ざった分布になっています。

これは完全な偶然ですが、今回のグラフは直感的には二峰性ではなさそうに見えるので、ベイズ推論の効果証明にぴったりではないでしょうか！

logsumexpの関数を作成

ではまず準備として、logsumexpを計算する関数を作成しておきます。

…とここで、「logsumexp」なんて本に出てきてなくね？と思ったそこのあなた！
その通りです。出てきません。笑

ですが今回のアルゴリズムでこの「logsumexp」が重要な役割を果たすんですよ！

まずこの関数は、書籍内の式(4.38)で使用します。

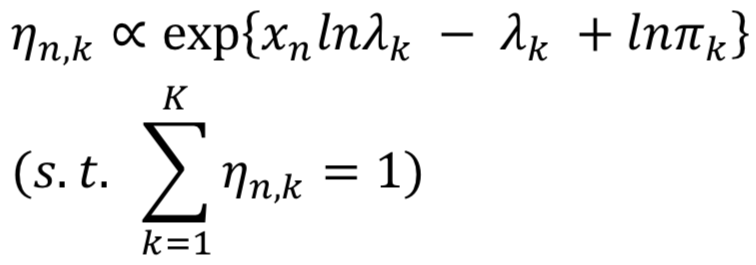
下段にηの条件式がある故に、logsumexpが必要になってきます。

実は普通に上段の式に沿ってηを計算した場合、ηは下段の条件式を満たさないので「正規化」する必要があります。
また今回の正規化では「合計値を1に揃える」操作なので、「各値を合計値で割る」必要があります。
よって上記に記載した式は、以下のように変形されます。

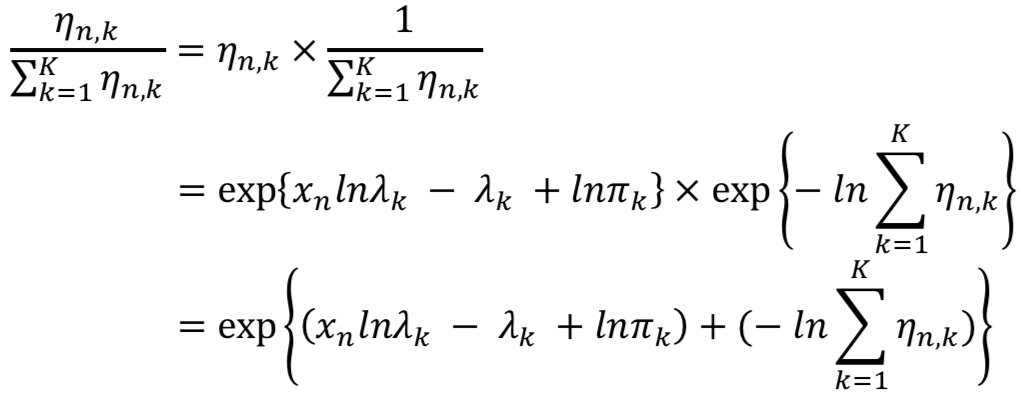
二段目の式は、
exp⁡(logx) = x
exp⁡(-logx) = -x
の公式から変形が可能です。

また三段目は指数法則を使えば容易ですね。
※ exp(n)は「eのn乗」を表します。

結果として、三段目の最後に正規化するための項が追加されています。
この正規化項をよく見ると、「log」「sum [=Σ]」「exp [=η]」が含まれていますよね！

そしてこの「logsumexp」を扱う場合、オーバーフローまたはアンダーフローを生じる可能性があるそうです…

よってオーバーフローやアンダーフローを事前に防ぐために、これから実装するlogsumexpの関数が必要になるのです！

長くなりましたが、関数自体は簡単なので早速実装しましょう。

def log_sum_exp(X):
    max_x = np.max(X, axis=1).reshape(-1, 1)
    return np.log(np.sum(np.exp(X - max_x), axis=1).reshape(-1, 1)) + max_x

私の実力ではこれ以上の説明ができないので、詳しくは「混合ガウス分布とlogsumexp」の記事などを確認してください。

ポアソン混合モデルをギブスサンプリングで近似推論

いよいよここからアルゴリズムを実装していきます！

今回は、『ベイズ推論による機械学習入門』に記載されている「アルゴリズム4.2 ポアソン混合モデルのためのギブスサンプリング」をPythonのnumpyベースで実装します。

# サンプリング用のリストを用意
sample_s = []
sample_lambda = []
sample_pi = []

# 定数の設定(繰り返し数, サンプル数, クラスタ数)
MAXITER = 100
N = len(X)
K = 2

# パラメータ初期値
init_Gam_param_a = 1
init_Gam_param_b = 1
init_Dir_alpha = np.ones(K)

# λ, πの初期値設定
Lambda = np.ones(K)
Pi = np.ones(K)

# πの条件に従って正規化(各値を合計値で割る)
if np.sum(Pi) != 1:
    Pi = Pi / np.sum(Pi)

# MAXITERの数だけ繰り返しサンプリング
for i in range(MAXITER):

    # sのデータ下地を準備
    s = np.zeros((N, K))

    # sをサンプルするためにηを算出
    log_eta = np.dot(X.reshape(N, 1), np.log(Lambda.reshape(1, K))) - Lambda.reshape(1, K) + np.log(Pi.reshape(1, K))

    # ηを正規化(logsumexp使ってオーバーフロー・アンダーフロー防ぐ)
    logsumexp_eta = -1 * log_sum_exp(log_eta)
    eta = np.exp(log_eta + logsumexp_eta)

    # ηをパラメータとしてカテゴリ分布からsをサンプル
    for n in range(N):
        s[n] = np.random.multinomial(1, eta[n])   
    # サンプルリストに追加
    sample_s.append(np.copy(s))


    # λをサンプルするためにa, bを算出
    Gam_param_a = (np.dot(s.T, X.reshape(N, 1)) + init_Gam_param_a).T[0]
    Gam_param_b = np.sum(s, axis=0).T + init_Gam_param_b

    # a, 1/bをパラメータとしてガンマ分布からλをサンプル
    Lambda = np.random.gamma(Gam_param_a, 1/Gam_param_b)
    # サンプルリストに追加
    sample_lambda.append(np.copy(Lambda))


    # πをサンプルするためにαを算出
    Dir_alpha = np.sum(s, axis=0) + init_Dir_alpha

    # αをパラメータとしてディリクレ分布からπをサンプル
    Pi = np.random.dirichlet(Dir_alpha)
    # サンプルリストに追加
    sample_pi.append(np.copy(Pi))

# クラスタは順不同(順番を定義していないため)
sample_s_ndarray = np.array(sample_s)
sample_lambda_ndarray = np.array(sample_lambda)
sample_pi_ndarray = np.array(sample_pi)

基本的に書籍通りに実装していますが、以下の点に注意が必要です。

・s, λ, πそれぞれをサンプリングする前に、各パラメータであるη, a, b, αを更新
・πは初期値の時に正規化が必要 (合計値で各値を割るだけ)
・ηはnp.exp()の中でlogsumexpと結合して正規化
・書籍ではNとKのfor文で回していますが、行列計算をすればfor文が必要なのはsのサンプリングの時だけ
・サンプルした値は対応する各リストに毎回追加

また、各パラメータの初期値は1とかで大丈夫です。(πだけ正規化に注意！)

サンプリング結果の確認

それでは順に結果を確認してみましょう！

…とその前に、クラスタが順不同であることに注意してください。
今回は偶然クラスタの設定順に結果が得られましたが、設定する順番と得られたクラスタ結果の順番は一致しないこともあります。ですがその場合も特に問題ありませんのでご安心を。

それではまず、λから確認します！

# 各クラスタの平均値
ave_Lambda = list(np.average(sample_lambda_ndarray, axis=0))

print(f'prediction: {ave_Lambda}')

結果は、以下のようになりました。
prediction: [29.921538459827033, 49.185569726045905]

λは各クラスタの平均値に該当します。
データの作成時、
Lambda_x1 = 30
Lambda_x2 = 50
と設定したので、かなりいい精度ではないでしょうか！

次にπを見てみましょう。

# 全データにおけるクラスタサンプル数の割合
ave_Pi = list(np.average(sample_pi_ndarray, axis=0))

all_samples = samples_x1 + samples_x2

print(f'prediction: {ave_Pi}')

結果は、以下の通りです。
prediction: [0.5801320180878531, 0.4198679819121469]

データ数に関しては、
samples_x1 = 300
samples_x2 = 200
と設定しました。
各値を全体のデータ数である500で割ると[0.6, 0.4]なので、ほぼ一致しています！

最後にsを確認して終わります！お疲れ様でした。

# 各クラスタ内のサンプル数
sum_s = np.sum(np.sum(sample_s_ndarray, axis=0), axis=0) / MAXITER

print(f'prediction: {sum_s}')

結果は、
prediction: [291.18 208.82]
となりました。

MAXITERの回数分だけ倍のサンプルが得られているため、MAXITERで各クラスタのサンプル合計を割れば得られます。

参考文献・参考リンク

『ベイズ推論による機械学習入門』
「混合ガウス分布とlogsumexp」