待ち行列理論 その3

前回の予告通りM/M/N/Nを考える。今回は待ち行列理論(著 大石 進一)を参考としています。

M/M/N/Nモデルとは

M/M/N/Nモデルはクライアントがポアソン分布に従って到着してサービスにかかる時間が指数分布に従うような、サーバーが1つのモデルである。行列の長さは最大で0です。これは行列ができないということを意味しています。サービスの規律は省略されてはいますがFCFSです。この系はアーランの呼損率システムとも呼ばれます。このモデルはこういった待ち行列ができないモデルにおいて基本的な考え方となりますので理解しておいた方がいいです。またこのモデルでは利用率が定義から$\rho=\frac{\lambda}{N\mu}$となるので注意してください。

系内にn人いる確率

まずポアソン過程に従ってクライアントが来ると仮定します。つまり十分短い時間間隔$\Delta t$には高々クライアントは1人しか来ないと仮定します。このとき平均到着率を$\lambda$とするとクライアントが1人来る確率は$\lambda \Delta t$と表すことができます。ここで時刻tに系内でクライアントがk人いる確率を$P_k(t)$とします。この確率の$\Delta t$後の変化を記述していきます。同様に平均サービス率が$\mu$のサーバーからクライアントが出ていく確率も$\mu \Delta t$となります。
ここまでは前回の仮定と同じです。今回はさらに状態kが$1\leq k \leq n$のときの平均サービス率を$k\mu$とします。これは平均サービス率$\mu$のサーバーがk台動いているときを意味しています。以降で系内のクライアントの数の変化を表す方程式（状態方程式）を考えます。しかし前回と同様に場合分けをして境界である$k=0,N$に注意して考えます。十分時間が経ち定常状態になったとして計算していくと
$P_k=\frac{\frac{a^k}{k!}}{\sum_{i=0}^{N}\frac{a^i}{i!}}$
ただし$(i=0,...,N), a=\frac{\lambda}{\mu}$となります。
これで系内にk人クライアントがいる確率がわかりました。
この後は待ち行列の初期の話で頻発する公式を求めてみます。

系内の平均客数 L

Lは平均値つまり期待値なので$L=\sum_{k=0}^{N}kP_k$から求めてやればいいことになります。よって$L=\sum_{k=0}^{N}kP_k$
$=a\frac{\sum_{k=0}^{N}\frac{a^k}{k!}-\frac{a^N}{N!}}{\sum_{k=0}^{N}\frac{a^k}{k!}}$
$=a(1-P_N)$

系内の平均待ち時間 W

リトルの公式から$W=\frac{L}{\lambda}=\frac{1-P_N}{\mu}$

待ち行列での平均客数 L_q

待ち行列ができないので0となります。

待ち行列の平均待ち時間 W_q

待ち行列に並べないので0となります。

#呼損率
呼損率とは待ち行列に並ぶことができなくて退去させられる人の割合を示します。普通$P_b$や$E_N(a)$と表記しますがここでは$E_N(a)$とします。呼損率はサーバが埋まっている確率と等しいので$E_N(a)=P_N$となります。これをアーラさんが見つけたためアーランB式と呼ばれています。余談ですがC式まであるそうです。
さらに面白いことに漸化式として
$E_0(a)=1$
$E_N=\frac{a E_{N-1}(a)}{s+a E_{N-1}(a)}$
が成り立ち、$F_N(a)=\frac{1}{E_N(a)}$と置くと
$F_0(a)=1$
$F_N(a)=1+\frac{N}{a}F_{N-1}(a)$
が成り立ちます。ともにNは１以上の整数です。

#通過した量Yと失われた量a_l
通過した量はつまり系内の平均客数です。つまり$Y=a(1-P_N)=a(1-E_N(a))$となります。このことから全体の平均aから通過した量を引いて失われた量を計算すると$a_l=a-Y=a E_N(a)$となります。

#aとNの関係
Bを0以上1以下の一定値として$E_N(a)=B$とする。このとき$E_N(a)$のaに関する偏微分方程式
$\frac{\partial E_N(a)}{\partial a}=(\frac{N}{a}-1+E_N(a))E_N(a)$
を$E_N(a)=B$という条件下で解いてあげることでaとNのを求めることができます。さらにNとaとBから利用率$\rho_N(B)=\frac{a(1-B)}{N}$が成り立つらしいです。
今回この二つをPythonでグラフを書いてみます。
これがプログラムとなります。

M_M_N_N.py

# -*- coding: utf-8 -*-
import matplotlib.pyplot as plt

# 無駄が多いプログラム

def E_B(N, a):
    # アーランB式を計算する。
    # Nはサーバー数
    # aはトラフィック密度
    p=1
    i=1
    while i < N+1:
       b = a * p
       p = b / (i + b)
       i += 1
    return p



def make_list(n, b):
    # nはサーバー数の最大値
    # bはニュートン法で解く為の目的関数E_B(N, a)-BのBを表していて呼損率を表す。
    p = [0 for i in range(n+1)]  # n+1番目がE_B(N, a)となる
    p[0] = 0  # a=s=0は明らかに成り立つ為
    c = 1  # a_0として初期値cを決める。
    for i in range(1, len(p)):
        a = c
        # E(N,a)=Bとなる値を20回程度の繰り返しで求める。
        for j in range(20):
            t = E_B(i, a)
            a = a - (t-b) / ((i/a-1+t)*t)
        p[i] = a
        c=a # 次回用に妥当な初期値に更新しておく

    return p


# ここからは描画と実行
n=50
b=0.01
p = make_list(n, b)

plt.figure()
plt.plot(range(n+1), p)
plt.xlabel("N")
plt.ylabel("a")
plt.title("E_N(a)=%.3f" % b)

plt.figure()
rho = [0]

for n, a in enumerate(p):
    if n == 0:
        continue
    rho.append(a*(1-b)/n)

plt.plot(range(n+1), rho)
plt.xlabel("N")
plt.ylabel("rho_N(B)")
plt.title("E_N(a)=%.3f" % b)

plt.show()

このプログラムによるとトラフィック密度aとサーバー数Nの関係は

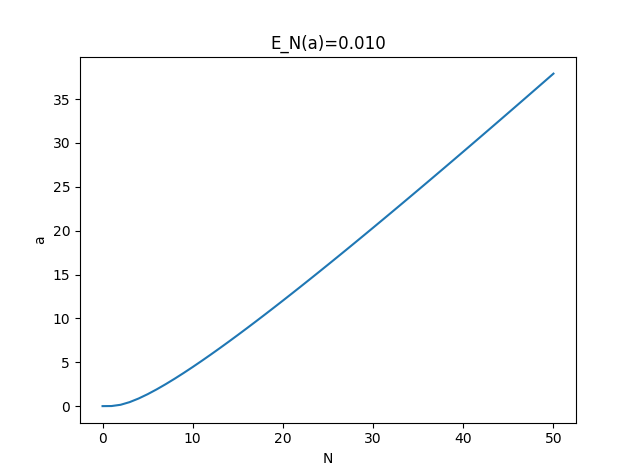
となり、Bを呼損率としたときの利用率$\rho_N(B)$は

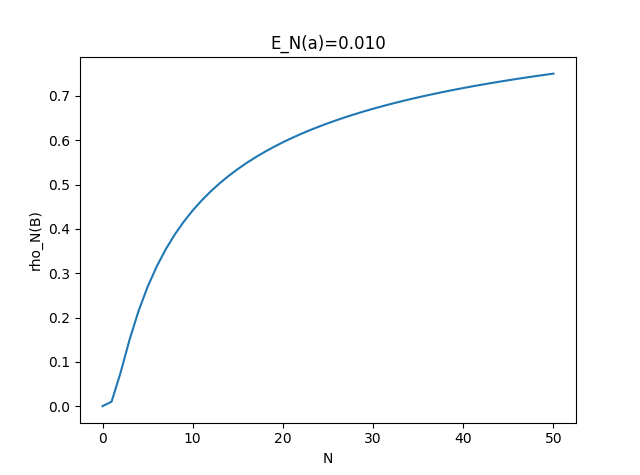
まとめ

今までこのシリーズではqiitaなのにプログラミングがなかったので入れてみました。
注意したいのは$0<\rho<1$の時で計算をしているのでそれ以外の値で計算をしてしまうと変な値になること。そしていまだ入門書を使って勉強中なので間違っている可能性があることです。
次回はどうしよう。