初めに
人と友好関係、交差点と道路、抵抗と電線などのように点と線で結び付いた網。つまりグラフがこの世にはあふれています。今回のフローネットワークはその中でも下水道網や回路などの何かを流すような用途のグラフが対象となります。ほかにも輸送路や交通網と、こちらも世の中にあふれかえっています。
また、簡略化のためにここでいうグラフは自己ループ(始点と終点が同じ頂点の有向辺)を許すが多重辺(同じ始点と終点を持つ有向辺)を持たない有向グラフとします。
フローネットワーク
まず詳しく話し始める前に定義をきちんとしておきましょう。
dfn: フローネットワーク
集合$V$、 集合$A$、 非負整数値をとる関数$l$、$u$ :: $A$->$\mathbb{Z}_{\gt 0}$、 実数値関数$c$ :: $A$ -> $\mathbb{R}$からなる組$N = (V, A, l, u, c)$を(整数)フローネットワークと呼ぶ。(つまり、フローネットワークは辺重み付き有向グラフの拡張としてとらえることができる。)
このとき$V$を$N$の頂点、$A$を$N$のエッジと呼び、エッジ$v \in A$に対して$l(v)$を$N$の$v$におけるフローの下限、$u(v)$を$N$の$v$におけるフローの上限、$c(v)$を$N$の$v$におけるフローのコストと呼ぶ。コストはエッジ上でフローが$1$単位分ながれた時の値です。つまり$v$上での最大のコストは$c(v)*u(v)$となります。$l$が常に$0$を返す定数関数の場合は$l$が省略される。そして、関数$l$と$u$を合わせて$N$の容量と呼ぶ。こちらも$l$が常に$0$を返す定数関数の場合は省略されて$u$のことを容量と呼ぶ。
さて数学的に定義できたのでこのフローネットワークをHaskellで実装していきます。実装すると次のようになります。
{-- 頂点数 --}
type VertexSize = Int
{-- 行列の内部型 --}
{-- フローに使う場合は非負整数として強制的に変換する --}
type Value = Int
{-- 正方行列 --}
type SquareMatrix = Matrix Value
{-- 隣接関係 --}
type Index = Int
type Adjacency = (Index, Index) -> Bool
{-- その他補助 --}
boolAsValue :: Bool -> Value
boolAsValue True = 1
boolAsValue False = 0
{-- フロー(補助) --}
asEdgeFlow :: Adjacency -> ((Index, Index) -> Value) -> (Index, Index) -> Value
asEdgeFlow adj flowFunc indices
= let v = (flowFunc indices) * (boolAsValue $ adj indices) in if v < 0 then 0 else v
flowMatrix :: VertexSize -> Adjacency -> ((Index, Index) -> Value) -> SquareMatrix
flowMatrix vSize adj flowFunc = matrix vSize vSize (asEdgeFlow adj flowFunc)
{-- ネットワーク --}
{-- 対象とする有向グラフは自己ループは許すが多重辺は許さない --}
data NetWork = NetWork {
vertexSize :: VertexSize,
adjacency :: Adjacency,
lower :: (Index, Index) -> Value,
upper :: (Index, Index) -> Value,
cost :: (Index, Index) -> Value
}
まずどのネットワーク内の関数でも対象としている頂点の個数と辺の隣接関係は固定なので最初に別々で保持しています。頂点はVertexSizeで1\ldots vertexSizeの個数の頂点を、エッジはAdjacency型として隣接している関係だけを定義しています。つまりエッジの関係の関数をadjacencyと置くと、頂点$i$から頂点$j$へ向かうエッジがあるときにadjacency (i, j) = Trueとなります。これは今回考えているのが多重辺を持たない有向グラフとしてのフローネットワークであるからできる方法で、多重辺を持つ場合はこの方法が使えないので注意してください。
フロー
さて流す土台となるフローネットワークは定義できたので、これから流す対象を定義していきます。まずは数学的な定義からです。
dfn: (整数)フロー
非負整数値関数$f$ :: $A$->$\mathbb{Z}_{\gt 0}$のことをフローと呼ぶ。
そしてフロー$f$がフローネットワーク$N$で流れる、つまり$\forall v \in A$で$l(v) \leq f(v) \leq u(v)$が成り立つとき$f$を許容フロー(feasible flow)と呼ぶ。
また、フローネットワーク$N$における許容フロー$f$のコストは$N$のコスト関数$c$を用いて
$\sum_{v \in A}{c(v)*f(v)}$
と定義される。
これらのHaskellでの実装はフローは関数、許容フローの判定はすべてのエッジで条件を満たすことを確認するだけなので省略する。
例
上のように定義してきたフローネットワークとフローの例として次のフローネットワークを考える。
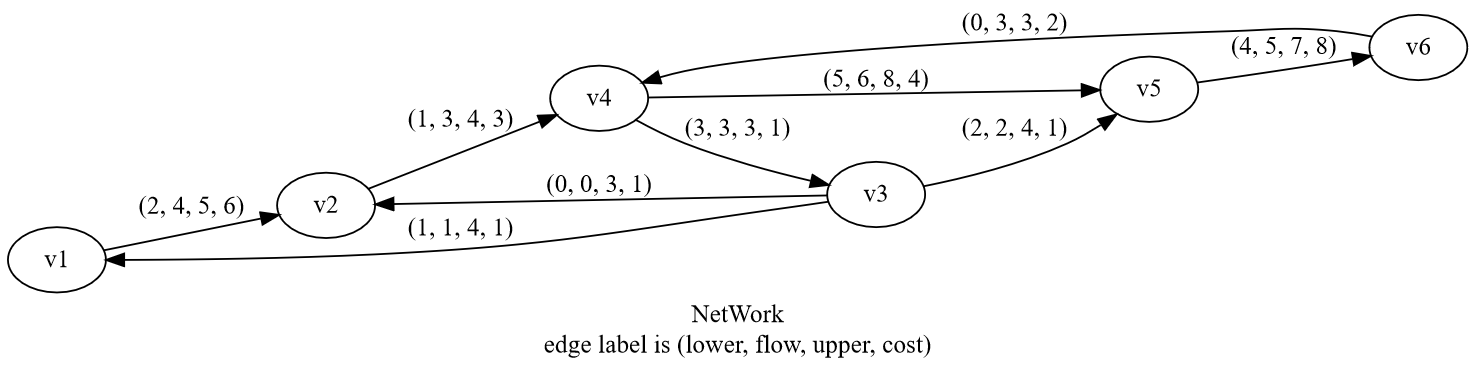
各辺のラベルは(lower flow, flow, upper flow, cost)を表している。
関数$g$に対して頂点$i$から頂点$j$にエッジがあるとき第$(i, j)$成分が$g(i, j)$となる行列(辺の場合は隣接行列のこと)で表すと次のようになる。
隣接行列(エッジの対応):
┌ ┐
│ 0 1 0 0 0 0 │
│ 0 0 0 1 0 0 │
│ 1 1 0 0 1 0 │
│ 0 0 1 0 1 0 │
│ 0 0 0 0 0 1 │
│ 0 0 0 1 0 0 │
└ ┘
下限フロー関数の行列:
┌ ┐
│ 0 2 0 0 0 0 │
│ 0 0 0 1 0 0 │
│ 1 0 0 0 2 0 │
│ 0 0 3 0 5 0 │
│ 0 0 0 0 0 4 │
│ 0 0 0 0 0 0 │
└ ┘
上限フロー関数の行列:
┌ ┐
│ 0 5 0 0 0 0 │
│ 0 0 0 4 0 0 │
│ 4 3 0 0 4 0 │
│ 0 0 3 0 8 0 │
│ 0 0 0 0 0 7 │
│ 0 0 0 3 0 0 │
└ ┘
コスト関数の行列:
┌ ┐
│ 0 6 0 0 0 0 │
│ 0 0 0 3 0 0 │
│ 1 1 0 0 1 0 │
│ 0 0 1 0 4 0 │
│ 0 0 0 0 0 8 │
│ 0 0 0 2 0 0 │
└ ┘
フロー関数の行列:
┌ ┐
│ 0 4 0 0 0 0 │
│ 0 0 0 3 0 0 │
│ 1 0 0 0 2 0 │
│ 0 0 3 0 6 0 │
│ 0 0 0 0 0 5 │
│ 0 0 0 3 0 0 │
└ ┘
許容フローか: True
フローのコスト: 109
ちなみに、フローはコストのほかにも各頂点に対して流出量と流入量の差を求めることもあります。これを各頂点ごとに計算した値を返す関数をバランスベクタと呼びます。なぜ関数なのにバランスベクタと呼ぶかというと、個人的には今回の例のように頂点をソートしてベクトル形式にできるときそのソート通りに並べてインデックスの指定で取得するのと関数にインデックスを指定して取得することが同値だからだと思います。
今回は、以下のようになりました。
バランスベクタ:
┌ ┐
│ 3 -1 0 3 -3 -2 │
└ ┘
バランスベクタの定義から推測できるように値が負の頂点は流出量より流入量が多く、このままいくと(物理的な問題だが)その頂点が耐え切れなくなったり、流れが滞ったりしてしまいます。つまり改善の余地がそこにあるわけですね。
応用例
フローネットワークとフローの代表的な応用例をここで紹介していきます。
まず一番有名なフロー最大化によるフローネットワークの限界量測定があります。これは下水道などでこのネットワーク(網)には最大どれくらいまで流せるかを測定せずに計算によって導くことに使われていたりします。最大がわかることで余力も簡単にですがわかったりするので広い目的で利用されている応用例ですね。
次に有名なのがフローのコスト最小化による費用最適化です。これは輸送経路網で経路によるコストを最小限に抑えるためなどで使われています。コストをガソリンと置き換えて道路交通網における渋滞時の燃料最小化として考えることもできます。
最後はあまり有名でないかもしれませんが、バランスベクタによるボトルネック予測です。例の最後にあったようにバランスベクタは流入量が多い頂点を推測するための指標になることができます。
終わりに
今回コード自体はあまり紹介できなかったのですが、コードはGitHubogata-k/network-introにすべて置いてあります。
フローネットワーク理論はインターネットのネットワークのトラフィック監視やオペレーションズ・リサーチの様々な分野で使われる横断的に利用可能な手法です。皆さんもぜひ遊んでみたらいかがでしょうか。
最後までお読みいただきありがとうございました。