はじめに
自分がROC曲線とAUCを理解できておらず、なかなか分かりやすい記事がなかったので自分で書きました。
先にまとめ
今回の話の要点をまとめると、以下のようになります。
- ROC曲線・AUCは分類問題に使用されるモデル評価指標である。
- ROC曲線・AUCは「正しく陽性と判断(=陽性率)できている」かつ「誤って陽性と判断(=偽陽性率)していない」モデルを良いモデルとして考えている。
- ROC曲線・AUCは不均衡データには特に不向きである。
ROC曲線の概要
ROC曲線とは、分類問題(「陽性/陰性」の判定、「犬/犬でない」の判定、など)でモデルを評価するためのグラフのことです。
以下のように、ROC曲線では横軸に偽陽性率、縦軸に陽性率をプロットしています。

↑これだけでは意味不明かと思いますので、以下でもっと丁寧に説明していきます~。
分類問題で"良いモデル"とは?→バランスの取れたモデル!
背景
分類問題を解くモデルを組んだとします。
例えば、ある疾病に罹っているか(陽性)・罹っていないか(陰性)を判断する機械学習モデルを作成したとします。
(例があった方が分かりやすいと思いますので、本記事ではこのような疾病の陽性判定の例を用いていきます。)
このとき、この陽性判定をする機械学習モデルが"良いモデル"かどうか判定したいです。
どのようなモデルが"良いモデル"と言えるのでしょうか?
"良いモデル"の定義
ここでは、
「正しく判定できる」と「誤って判定しない」をバランスしたモデル
を良いモデルと考えます。
一見、「正しく判定できる」と「誤って判定しない」はイコールな事象(正しく判定できれば、誤った判定は減る)ように思えますが、実際はそうでもなく、トレードオフの関係(正しく判定できるほど、誤って判定が増える)になりえます。
先ほどの疾病の陽性判定の事例で考えてみましょう。
ある疾病があります。この疾病は非常にリスクの高い疾病で、陽性の場合は早急な処置が必要です。処置が少しでも遅れると死にます。
ですので、(少なくとも1次的な検査としては)間違っても良いから、なるべく陽性と判定しやすいようにしたいです(なぜなら、本当は陽性なのに陰性と判定してしまったら、処置が遅れるからです)。
このように陽性と判定しやすいようにすると、少なくとも「正しく判定(=陽性の患者に対して、正しく陽性と判定)」できます。
しかし、このように陽性と判定しやすくしてしまうと、ただの風邪の人でも陽性と判定してしまうような「誤った判定(=本当は陰性なのに、陽性と判定)」をしてしまうケースが起こりやすくなります。
このように、「正しく判定できる」ことと「誤って判定しない」ことはトレードオフの関係にあるのです。
このようなトレードオフの中で、両方をバランスしたモデルが"良いモデル"であると考えます。
正しい判定=陽性率、誤った判定=偽陽性率である!
「正しい判定」と「誤った判定」をもう少し具体化する
さきほどの例でもあったように、「正しい判定」と「誤った判定」を以下のように定義します。
- 正しい判定:陽性率(=実際は陽性である患者に対して、どれだけ正しく陽性と判定できたか)
- 誤った判定:偽陽性率(=実際は陰性である患者に対して、どれだけ誤って陽性と判定しまったか)
ROC曲線では縦軸に陽性率、横軸に偽陽性率を描くことで、このトレードオフをグラフ上で表現します。
ちなみに、
"陽性率"は陽性患者をどれほど陽性とみなすかを示す「病気の人を検出する力」で感度とも呼ばれ、
"1-偽陰性率"は陰性患者をどれほど陰性とみなすかを示す「病気でない人を検出する力」で特異度とも呼んだりします。
偽陽性率と陽性率を理解しやすくしよう!→混同行列
先ほど陽性率と偽陽性率という言葉が出てきましたが、言葉だけだと少し考えづらいです。
そこで、「混同行列」という表を用いると理解しやすくなります。
混同行列は以下のようなもので、横軸に予測値、縦軸に正解値(真の値)で表現され、各象限の件数を表形式で示したものです。

混同行列でも同様に、陽性率と偽陽性率を以下のように定義できます。
- $陽性率=\cfrac{「実際に陽性」であり、「正しく陽性」と判定できた件数}{「実際に陽性」である件数}$
- $偽陽性率=\cfrac{「実際に陰性」であるのに、「誤って陽性」と判定した件数}{「実際に陰性」である件数}$
混同行列を考えると、陽性率・偽陽性率でどこを見ているか分かりやすくなります。
実際にROC曲線を描画してみる
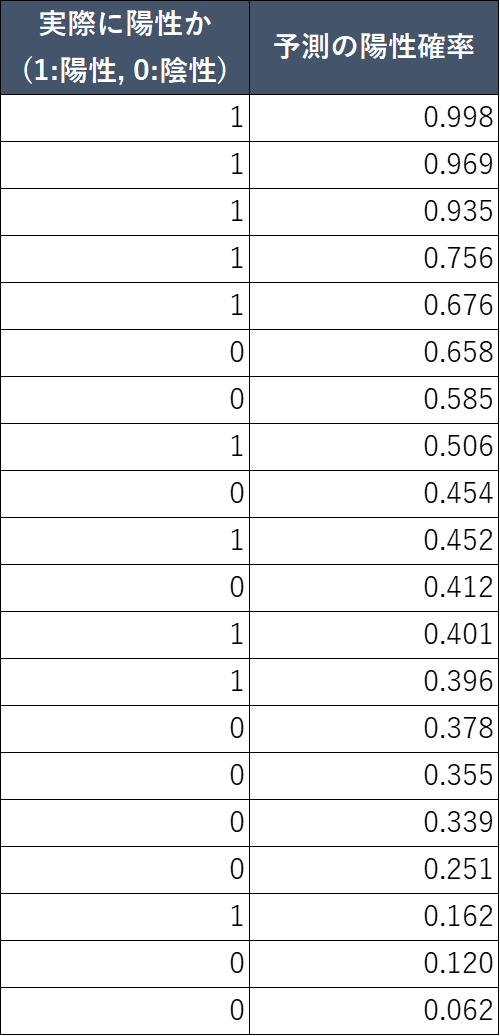
与えらえているデータ→陽性"確率"のデータ!
実際に陽性判定をする機械学習モデルを組んだ場合、以下のように陽性確率がアウトプットデータとして出力されます。
このアウトプットデータを用いて、ROC曲線を描いていきましょう。
陽性率・偽陽性率を出すには、閾値を設定する必要がある
さっそくROC曲線を描いていきたいのですが、以下でROC曲線を描く際の思想を説明します。
さきほど「ROC曲線では縦軸に陽性率、横軸に偽陽性率を描く」と言いましたが、
このようなアウトプットデータで陽性率と偽陽性率を描くには、(混同行列にもあったように)予測も陽性と陰性を分けないといけません。つまり、「予測の陽性確率がXX%以上は陽性とする」みたいな、陽性の判定基準(閾値)が必要です。
しかし、閾値は一意に定まるわけではないので、陽性判定の閾値を0-100%の間で変化させることで、ROC曲線を描きます。
このように陽性と陰性の閾値を変化させることで、様々な状況でどのようにモデルが挙動するかを全体的に見ることができます。
↑とはいえ、まだ想像しづらいと思いますので、以下で実際に描いてみます。
実際に描いてみる
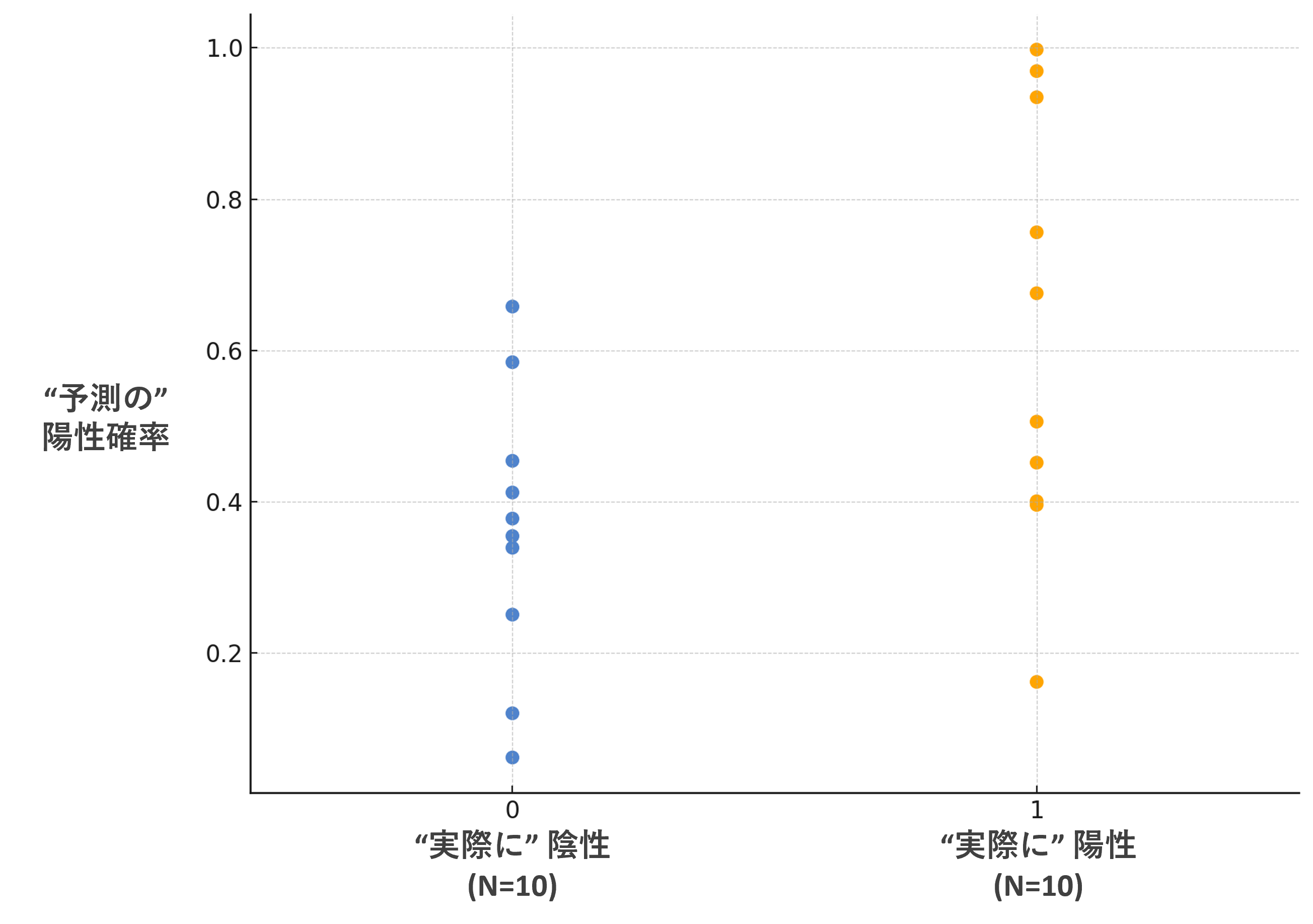
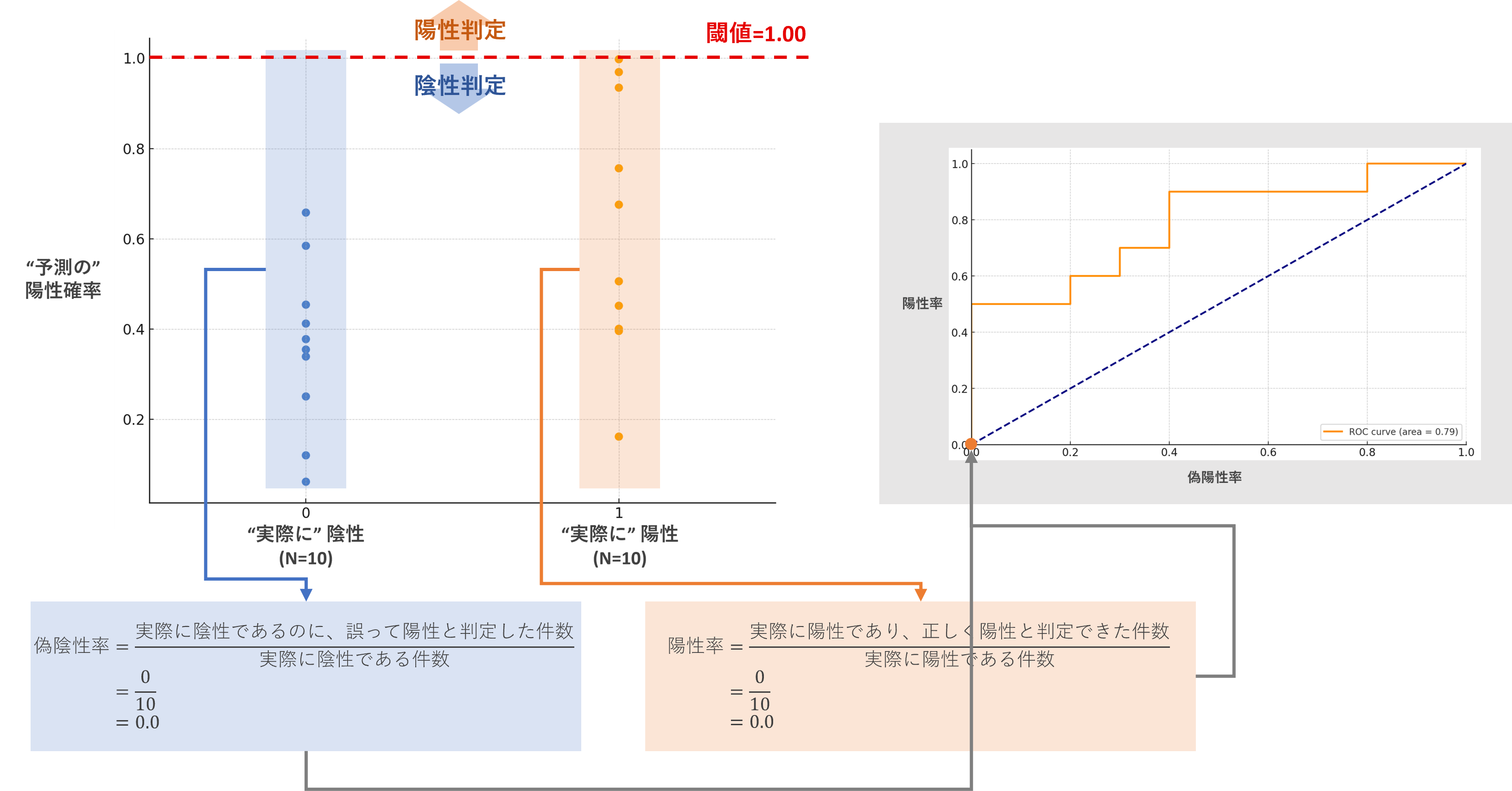
先ほど表で見せたデータをグラフ化すると、以下のようになります。
横軸には「実際に陽性だったか」、縦軸には「予測の陽性確率」をプロットしています。
実際に陽性だった患者/陰性だった患者はそれぞれ10名ずつです。
このとき、実際に閾値を変化させてROC曲線を描いていきましょう。
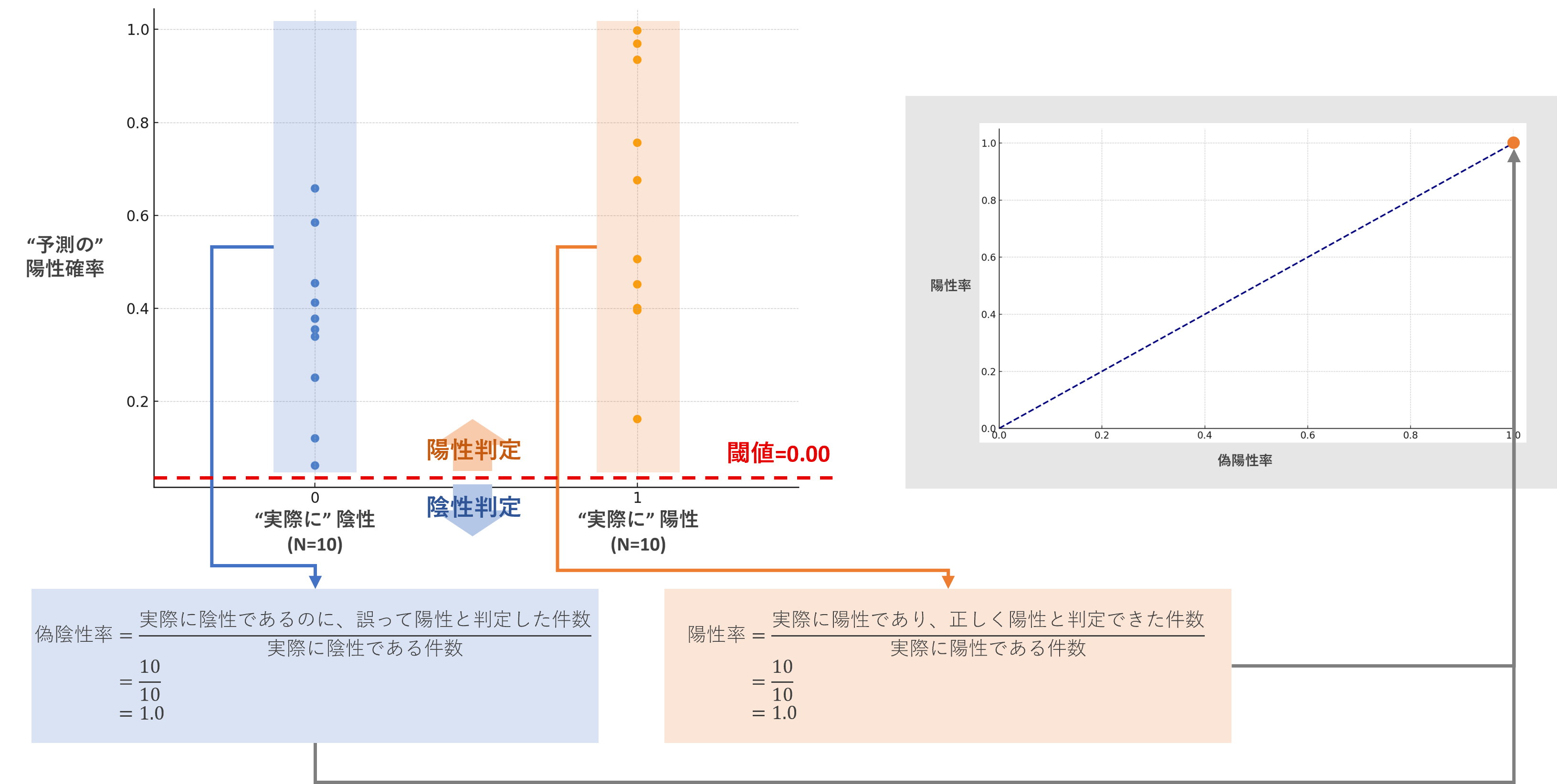
①閾値=0.00のとき
このとき、
- 陽性率:陽性の顧客は10件全て陽性と判断できているので、陽性率は1.0です。
- 偽陰性率:陰性の患者は10件全て誤って陽性と判断しているので、偽陰性率は1.0です。
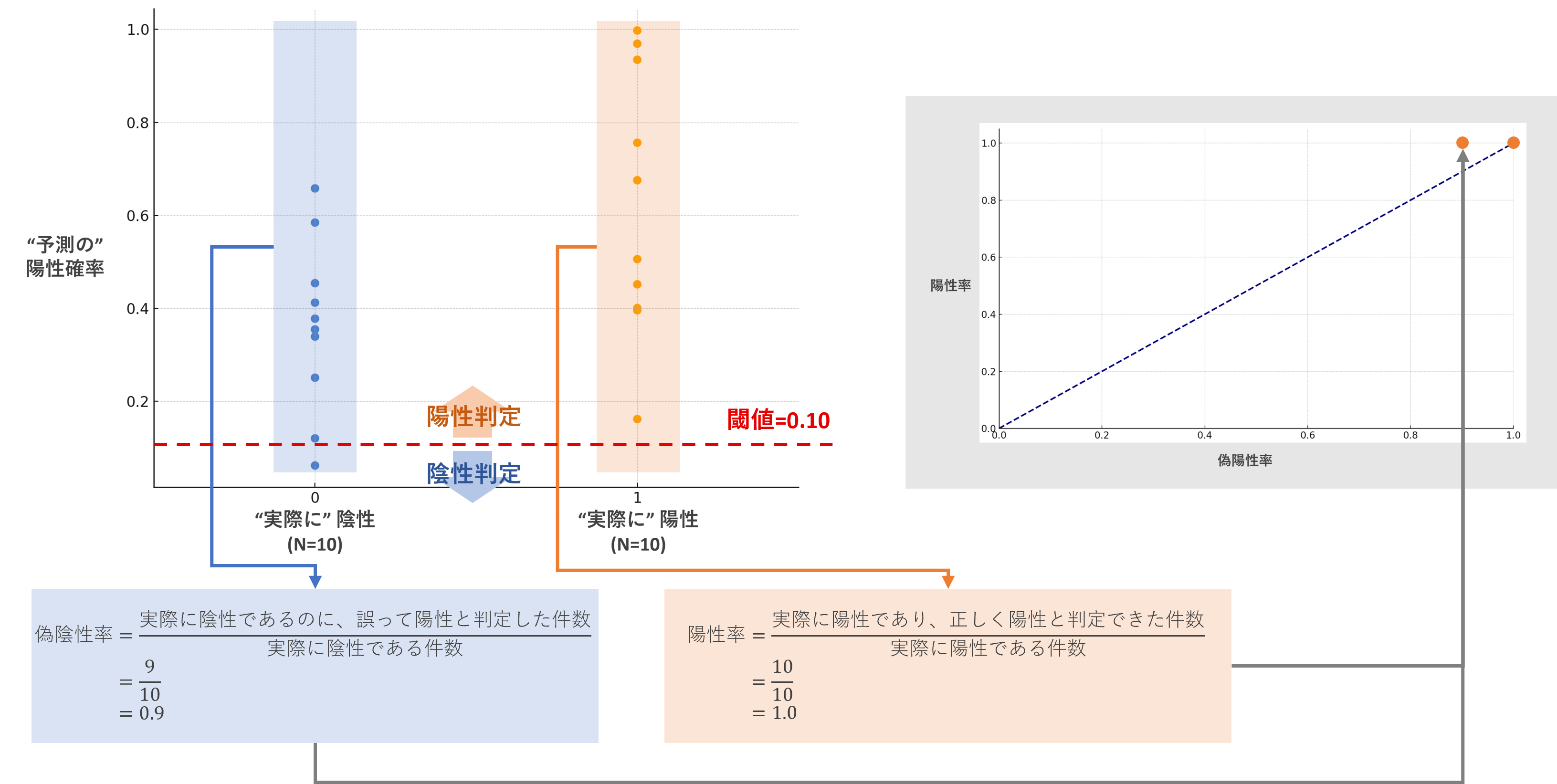
②閾値=0.10のとき
このとき、
- 陽性率:陽性の顧客は全て陽性と判断できているので、陽性率は1.0です。
- 偽陰性率:陰性の患者は9件誤って陽性と判断しているので、偽陰性率は0.9です。
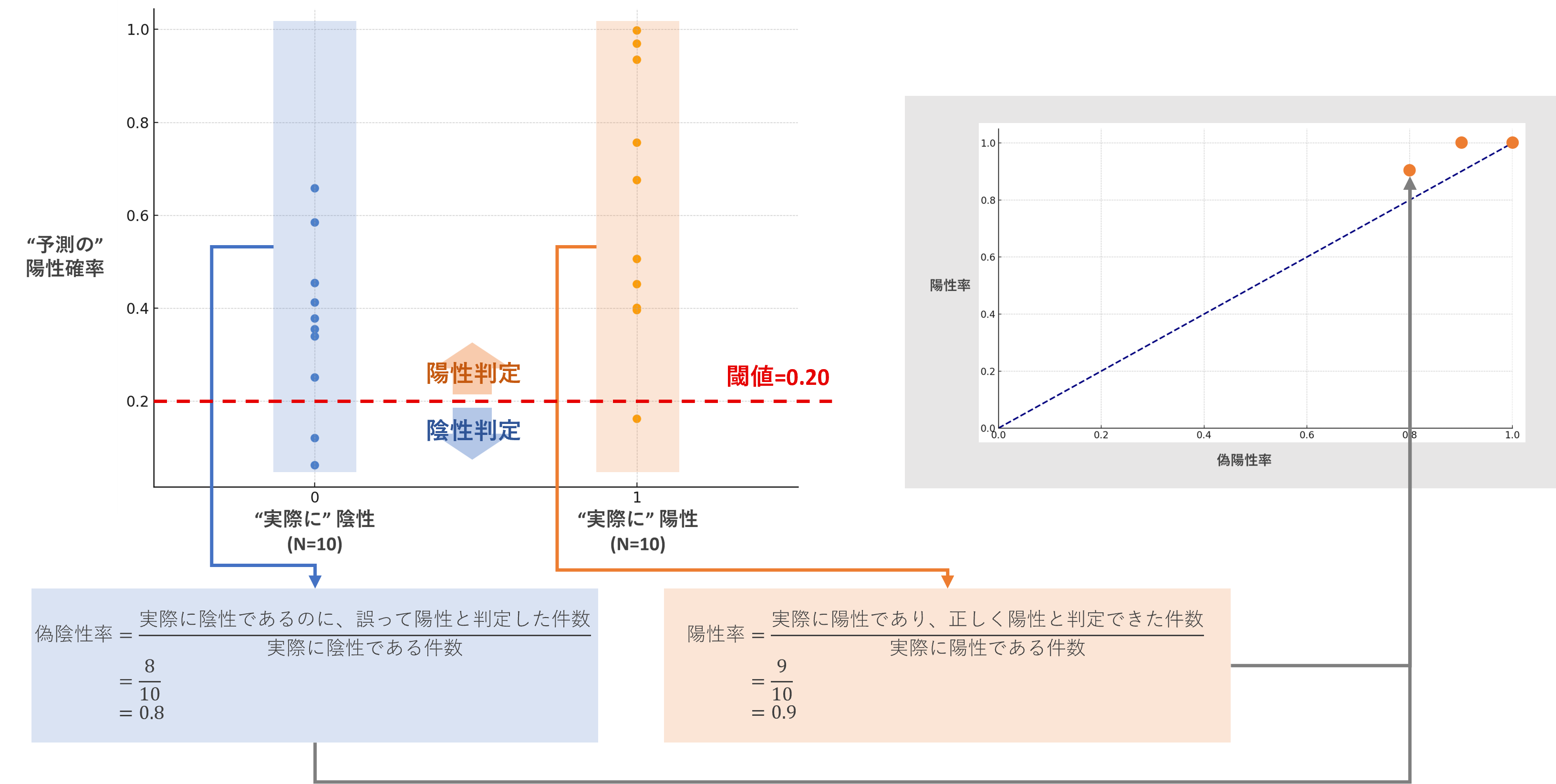
③閾値=0.20のとき
このとき、
- 陽性率:陽性の顧客は9件陽性と判断できているので、陽性率は0.9です。
- 偽陰性率:陰性の患者は8件誤って陽性と判断しているので、偽陰性率は0.8です。
...
このようにプロットしていくと、最後閾値1.00のとき、以下のように描けます。
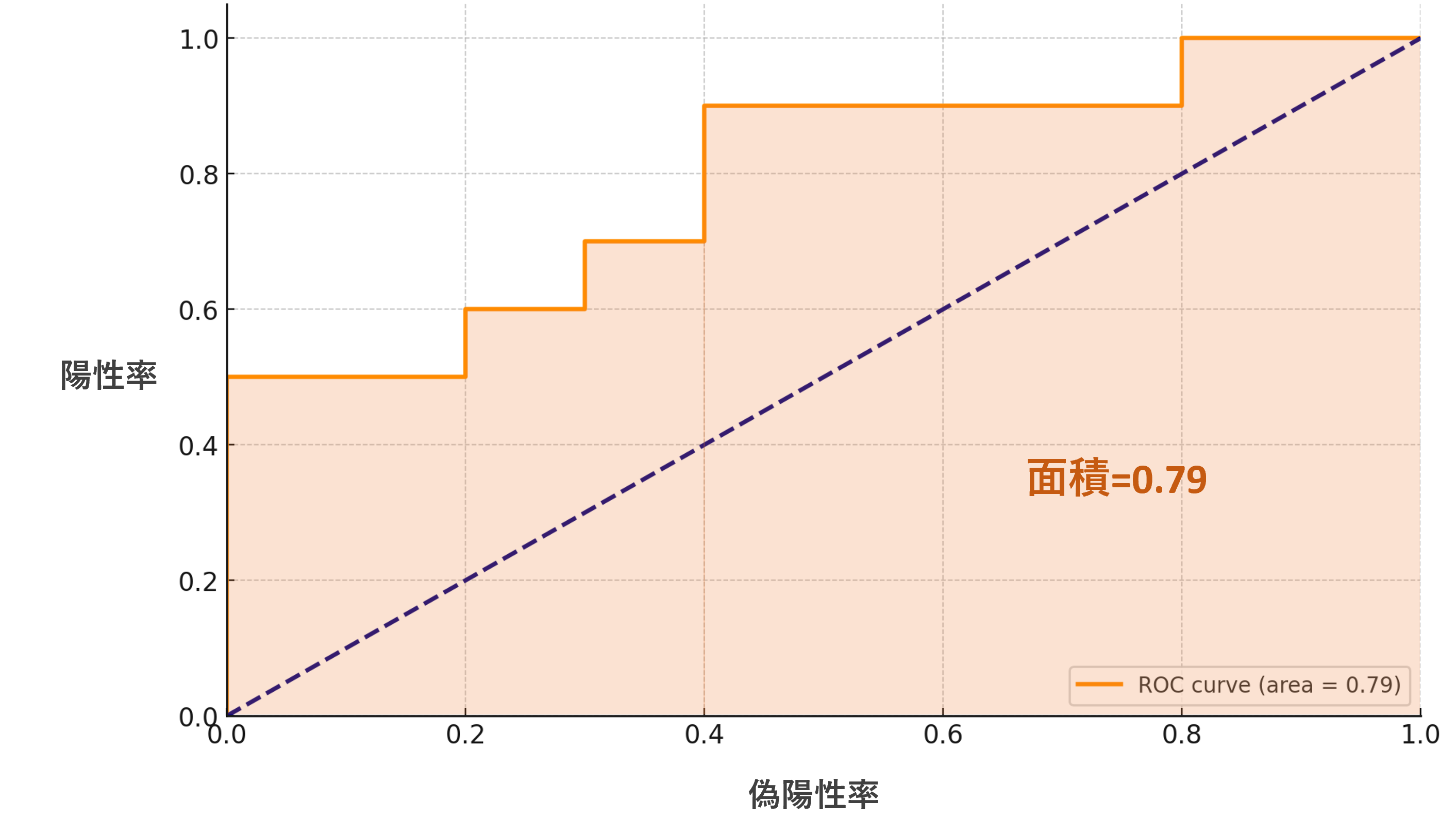
ROC曲線が描けました。
AUC
AUCとは、このROC曲線の下の部分の面積です。
0から1の間の値を取り、1に近いほど、陽性率と偽陽性率をバランスできている、すなわち精度が良いことになります。
精度の目安ですが、
- AUC≧0.80:精度が高い
- 0.70≦AUC<0.80:精度はまぁまぁ高い
- 0.60≦AUC<0.70:微妙
- AUC<0.60:ゴミ
- (AUC<0.50:もはや逆の予測をしてしまっている)
(データによりますので、あくまでも参考値です)
注意点
不均衡データには不向き
不均衡データ(実際に陽性の患者が極端に多い or 実際に陰性の患者が極端に多い)では、AUCが高く出る傾向にあります。
例えば、実際に陰性だった患者の割合が99%、実際に陽性だった患者の割合が1%のデータがあったとします。このとき、ほとんどの患者を陰性と判断するモデルを組めば、多数の陰性サンプルを正確に予測するモデルになるので、偽陽性率が下がり、グラフは左に張り付くことからAUCが高くなります。
このように、不均衡データではAUCが高く出るため、スコアとして不向きです。
不均衡データでは、AUCだけでなく、PR曲線やF1スコアを用いることが多いです。
他の評価指標と合わせて総合的に判断すべし!
これは分類問題だけではなくモデリング全体に言えることですが、
不均衡データでなくとも、モデルの精度を評価する際には他の指標と合わせて確認するのが良いです。
研究・ビジネス上の目的と合わせて評価指標は吟味しましょう。
まとめ(再掲)
今回の話の要点をまとめると、以下のようになります。
- ROC曲線・AUCは分類問題に使用されるモデル評価指標である。
- ROC曲線・AUCは「正しく陽性と判断(=陽性率)できている」かつ「誤って陽性と判断(=偽陽性率)していない」モデルを良いモデルとして考えている。
- ROC曲線・AUCは不均衡データには特に不向きである。