問題
既存投稿一覧ページへのリンク
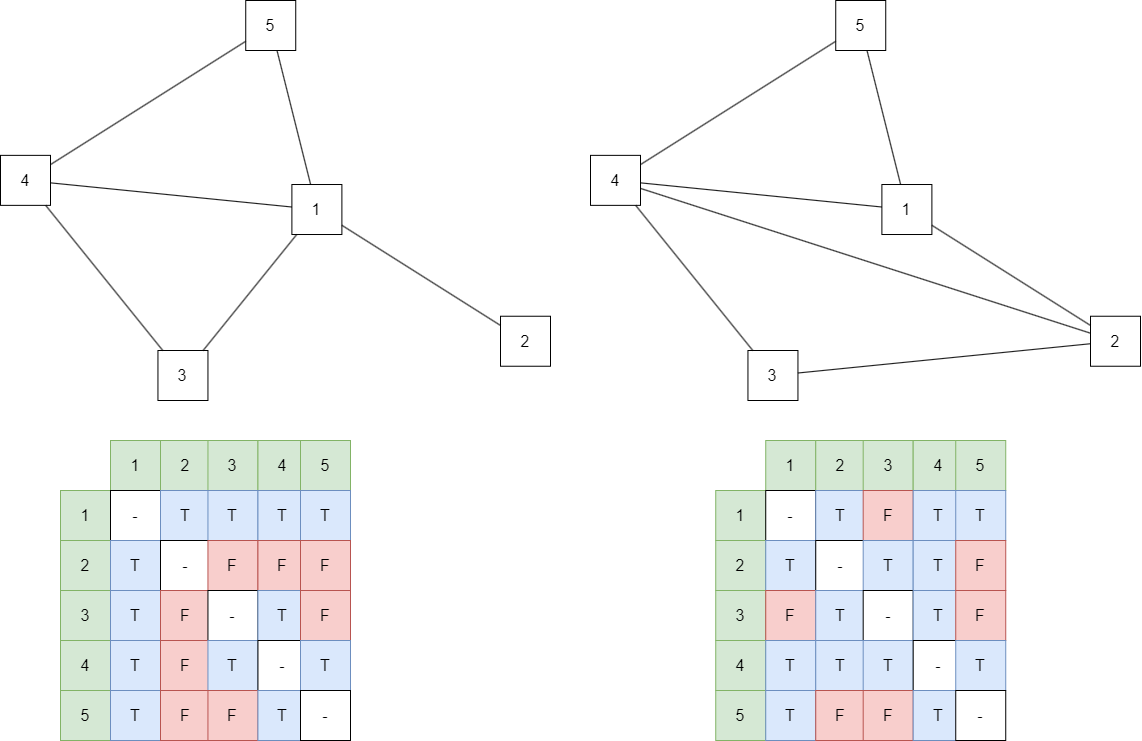
解法手順1
1. 入力データの処理
まず、入力から以下の情報を取得する
- グラフ $ G $ の辺情報 ($ edge_G $)。
- グラフ $ H $ の辺情報 ($ edge_H $)。
- 辺を追加または削除する際のコスト行列 ($ cost_{matrix} $)。
これらのデータは関数 io_func() によって処理される。
具体的には以下の形式でデータが格納される。
-
edge_Gおよびedge_Hは隣接行列として表現され、頂点間に辺がある場合はTrue、ない場合はFalse。 -
cost_matrix[i][j]は頂点 $ i $ と $ j $ の間で操作を行う際のコスト。
2. 全ての頂点順列を試す
次に、頂点の順列を試してグラフ $ H $ を変換する。
順列について
- 順列によって、グラフ $ H $ の頂点番号を対応させることで、グラフ $ G $ と比較します。
コスト計算
各順列について以下を行います：
- 順列に基づいてグラフ $ H $ を変換。
- 頂点ペア $ (i, j) $ ごとに、$ edge_G[p[i]][p[j]] \neq edge_H[i][j] $ の場合、コストを加算。
- つまり、グラフ構造が一致しない部分について操作コストを計算する。
- 現在の順列で得られたコストが最小値より小さい場合、それを更新する。
この処理によって、全ての可能な対応関係を考慮した上で最小コストが求められる。
解法の流れまとめ
-
入力処理:
- グラフ情報とコスト行列を読み取る。
-
全順列探索:
- 頂点番号の並べ替えによる全ての対応関係を試す。
-
コスト計算:
- グラフ構造が一致しない部分について操作コストを加算。
-
最小値更新:
- 各順列で得られたコストから最小値を選択する。
-
結果出力:
- 最小コストを出力する。
メモ
問題の解法を思いつくためのステップ。
1. 問題の本質
まず、問題文から、以下の点を読み取る
- 目標: グラフ $ G $ と $ H $ を同型にするための最小コストを求める。
- 操作: 頂点ペア $ (i, j) $ の辺を追加または削除し、そのコストが与えられる。
- 制約: グラフ同型とは、頂点の対応関係が存在し、辺の接続状態が一致すること。
この段階で、「頂点の対応関係を試行しながらコストを計算する必要がある」と理解する。
2. 解法の方向性を検討する
- 頂点の対応関係（順列）を試す。
- 対応関係に基づいて、グラフ $ H $ を変換して $ G $ と比較する。
- 不一致部分についてコストを計算し、最小値を求める。
このとき、「全ての頂点順列を試す」という発想は、グラフ同型性の定義から自然に導かれる。
また、「不一致部分のコスト計算」は問題文で与えられた操作条件に基づく。
3. 順列全探索という手法に気づく
グラフ同型性の問題では、頂点間の対応関係（順列）を試すことが基本的なアプローチ。
- 順列は $ N! $ 通り存在するため、小規模な $ N $ に対しては全探索が可能。
- 各順列について、辺の一致・不一致を確認し、不一致部分のコストを加算する。
このような「順列全探索 + コスト計算」という手法は、グラフ同型性や組合せ最適化問題で一般的なもの。
4. コスト計算方法を具体化する
次に、不一致部分について具体的なコスト計算方法を考えます：
- 順列 $ P $ に基づいて、グラフ $ H $ を変換。
- 辺 $ (i, j) $ ごとに、$ edge_G[P[i]][P[j]] \neq edge_H[i][j] $ を確認。
- 不一致の場合、コスト行列 $ cost_matrix[i][j] $ の値を加算。
まとめ
この解法は以下のような流れで思いつく
- 問題文から「頂点間対応関係（順列）の全探索」が必要と判断。
- グラフ同型性と操作条件から「不一致部分のコスト計算」を具体化。
- 計算量や実装可能性から「順列全探索 + コスト計算」が有効と判断。
ACコード1
ac.py
import itertools
import logging
# ロガーのセットアップ
def setup_logger(debug_mode):
logger = logging.getLogger(__name__)
if not logger.handlers: # ハンドラが存在しない場合のみ追加
logger.setLevel(logging.DEBUG if debug_mode else logging.INFO)
formatter = logging.Formatter('%(asctime)s - %(name)s - %(levelname)s - %(message)s')
file_handler = logging.FileHandler('program_trace.log', encoding="utf8")
file_handler.setFormatter(formatter)
logger.addHandler(file_handler)
logger.debug(f"ロガーのセットアップが完了しました。デバッグモード: {debug_mode}")
return logger
# 標準入力を処理する関数
def io_func():
n = int(input())
mg = int(input())
edge_G = [[False for _ in range(n)] for _ in range(n)]
for _ in range(mg):
u, v = map(int, input().split())
u -= 1
v -= 1
edge_G[u][v] = True
edge_G[v][u] = True
mh = int(input())
edge_H = [[False for _ in range(n)] for _ in range(n)]
for _ in range(mh):
a, b = map(int, input().split())
a -= 1
b -= 1
edge_H[a][b] = True
edge_H[b][a] = True
cost_matrix = [[0 for _ in range(n)] for _ in range(n)]
for i in range(n - 1):
row = list(map(int, input().split()))
for j, cost in enumerate(row):
cost_matrix[i][i + j + 1] = cost
cost_matrix[i + j + 1][i] = cost
return n, edge_G, edge_H, cost_matrix
# 問題を解く関数
def solve(n, edge_G, edge_H, cost_matrix, logger):
INF = 1 << 30
result = INF
# 全ての頂点の順列を試す
for permutation in itertools.permutations(range(n)):
cost = 0
logger.debug(f"現在の順列: {permutation}")
# 順列に基づいてコスト計算
for i in range(n):
for j in range(i + 1, n):
if edge_G[permutation[i]][permutation[j]] != edge_H[i][j]:
cost += cost_matrix[i][j]
logger.debug(f"辺 ({i}, {j}) の不一致: コスト {cost_matrix[i][j]} を加算 (累積コスト: {cost})")
result = min(result, cost)
logger.debug(f"現在の最小コスト: {result}")
print(result)
# メイン関数
def main():
debug_mode = False # 必要に応じてTrueに変更可能
logger = setup_logger(debug_mode)
# 入力処理
n, edge_G, edge_H, cost_matrix = io_func()
# 問題解決
solve(n, edge_G, edge_H, cost_matrix, logger)
if __name__ == "__main__":
main()