問題
要約
- N頂点の木が与えられる。
- 頂点には1からNまでの番号が付いている。
- 辺は頂点AiとBiを結んでいる。
- この木から辺と頂点を削除して新しい木を作る。
- 新しい木は指定されたK個の頂点(V1, ..., VK)を全て含む必要がある。
条件を満たす新しい木の中で、頂点数が最小のものを求める。
- N: 元の木の頂点数
- Ai, Bi: i番目の辺が結ぶ2つの頂点の番号
- K: 新しい木に必ず含める必要がある頂点の数
- V1, ..., VK: 新しい木に必ず含める必要がある頂点の番号
既存投稿一覧ページへのリンク
アプローチ
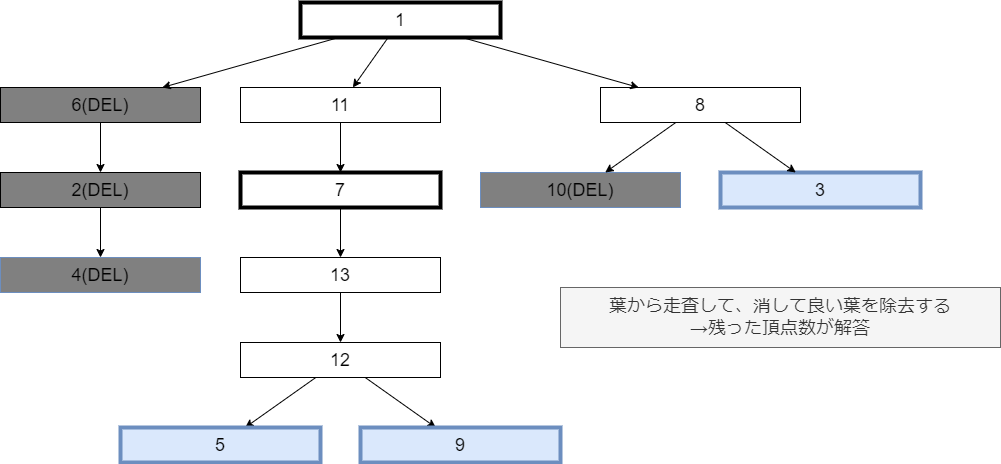
最小の部分木を見つけるために、元の木から不要な頂点を削除していく
解法手順
- 入力から木の構造を隣接リストとして構築する。
- 必要な頂点(V1, ..., VK)を記録する配列を作成する。
- 全ての頂点を初期状態で「残す」としてマークする。
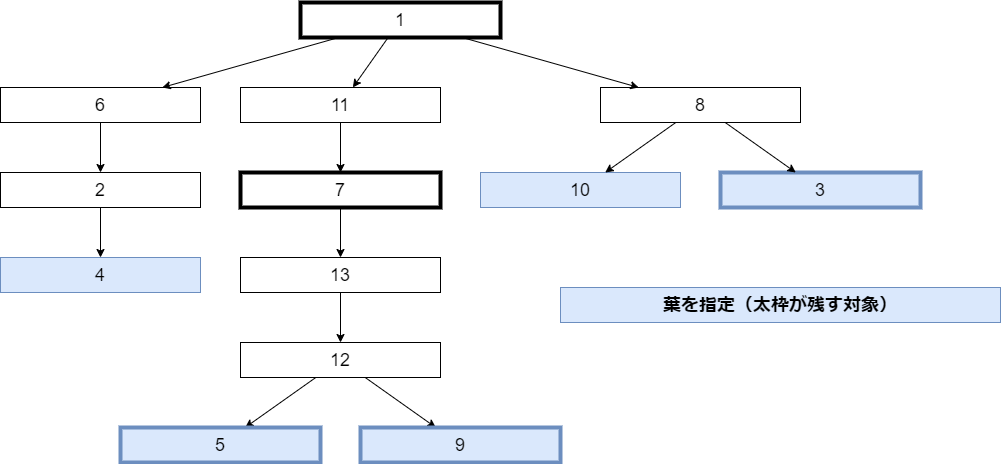
- 葉ノード(隣接する頂点が1つだけの頂点)を特定し、リストに追加する。
- 葉ノードのリストが空になるまで以下の処理を繰り返す:
a. リストから葉ノードを取り出す。
b. その葉ノードが必要な頂点でなければ、以下の処理を行う:- その頂点を「削除」としてマークする。
- その頂点と隣接する唯一の頂点との接続を解除する。
- 接続を解除した結果、新たに葉ノードになった頂点があれば、それをリストに追加する。
- 最後に、「残す」とマークされた頂点の数を数え上げ、それを答えとして出力する。
ACコード
ac.py
from collections import defaultdict
def io_func():
# 入力を受け取る
N, K = map(int, input().split()) # Nは頂点数、Kは必要な頂点の数
edges = [map(int, input().split()) for _ in range(N-1)] # 辺の情報
v = list(map(int, input().split())) # 必要な頂点のリスト
return N, K, edges, v
def solve(N, K, edges, v):
# 隣接リストを作成
d = defaultdict(set)
for a, b in edges:
d[a-1].add(b-1)
d[b-1].add(a-1)
# 必要な頂点を記録
V = [0] * N
for i in v:
V[i-1] = 1
# 全ての頂点を初期状態で「残す」としてマーク
ans = [1] * N
# 葉ノードを特定し、リストに追加
L = set()
for i in range(N):
if len(d[i]) == 1:
L.add(i)
# 葉ノードの処理
while L:
p = L.pop() # 葉ノードを取り出す
if V[p] == 1:
continue # 必要な頂点なら削除しない
else:
ans[p] = 0 # 不要な頂点を削除
q = d[p].pop() # 隣接する唯一の頂点
d[q].remove(p) # 接続を解除
if len(d[q]) == 1:
L.add(q) # 新たな葉ノードをリストに追加
# 残された頂点の数を返す
return sum(ans)
if __name__=="__main__":
# メイン処理
N, K, edges, v = io_func()
result = solve(N, K, edges, v)
print(result)
# ###
# N: 頂点の総数
# K: 必要な頂点の数
# edges: 辺の情報を格納したリスト
# v: 必要な頂点のリスト
# d: 隣接リスト(各頂点に隣接する頂点の集合)
# V: 各頂点が必要かどうかを示す配列(1:必要、0:不要)
# ans: 各頂点を残すかどうかを示す配列(1:残す、0:削除)
# L: 処理すべき葉ノードの集合
# 1. io_func関数で入力を受け取る。
# 2. solve関数で主な処理を行う。
# a. 隣接リストdを作成し、木の構造を表現する。
# b. 必要な頂点を配列Vに記録する。
# c. 全ての頂点を初期状態で「残す」としてマークする(ans配列)。
# d. 葉ノードを特定し、集合Lに追加する。
# e. 葉ノードの処理を行う:
# - 葉ノードが必要な頂点でなければ削除する。
# - 削除した結果、新たに葉ノードになった頂点があれば、それをLに追加する。
# f. 残された頂点の数(ansの合計)を返す。
# 3. メイン処理で入力を受け取り、solve関数を呼び出し、結果を出力する。
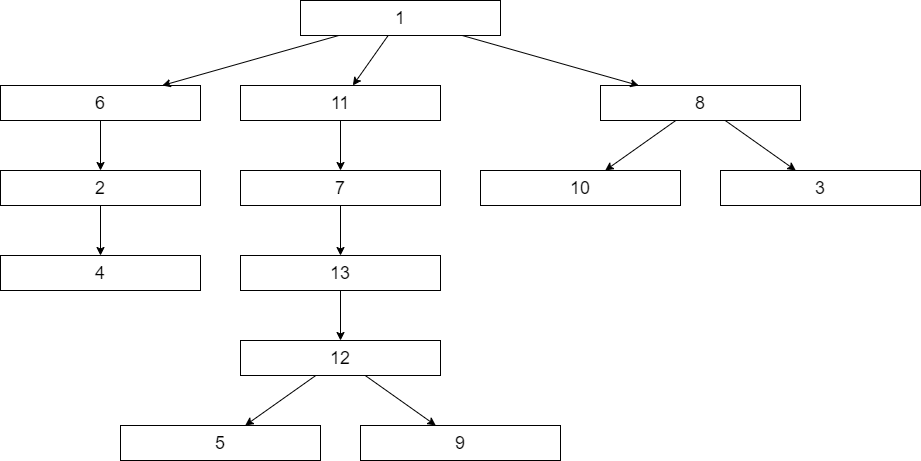
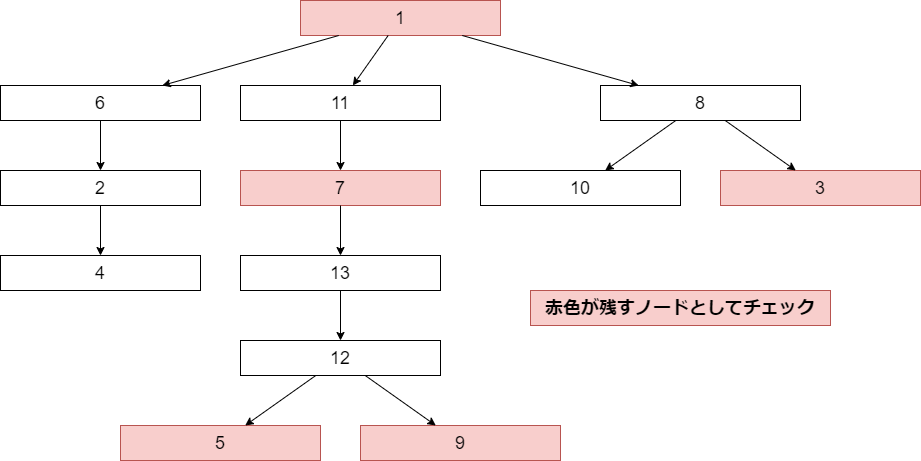
解法イメージ
N = 13
K = 5
edges = [(1, 6), (6, 2), (1, 11), (11, 7), (1, 8), (7, 13), (8, 10), (8, 3), (13, 12), (12, 5), (12, 9), (2, 4)]
v = [1, 3, 5, 7, 9]