問題
既存投稿一覧ページへのリンク
優先度付きキュー基本操作
sample.py
from heapq import heappush, heappop
def priority_queue_operations():
heap = []
heappush(heap, (5, 'A'))
heappush(heap, (3, 'B'))
heappush(heap, (7, 'C'))
result = []
while heap:
result.append(heappop(heap))
return result
print(priority_queue_operations()) # [(3, 'B'), (5, 'A'), (7, 'C')]
ダイクストラのメインループ
sample.py
from heapq import heappush, heappop
def dijkstra_step():
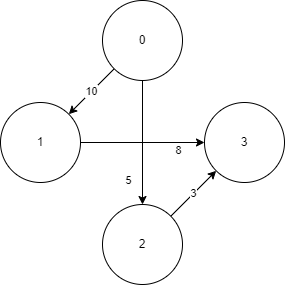
graph = [
[(1, 10), (2, 5)], # ノード0の隣接
[(3, 8)], # ノード1の隣接
[(3, 3)], # ノード2の隣接
[] # ノード3の隣接
]
dist = [0, 10**18, 10**18, 10**18]
heap = [(0, 0)]
while heap:
d, v = heappop(heap)
if d > dist[v]:
continue
for u, w in graph[v]:
if d + w < dist[u]:
dist[u] = d + w
heappush(heap, (dist[u], u))
return dist
print(dijkstra_step()) # [0, 10, 5, 8]
ノードの重み計算
sample.py
def calculate_node_weight():
A = [0, 3, 5, 2, 4] # 各ノードの追加重み
edges = [(1, 2, 10), (2, 3, 5), (1, 3, 8)]
weighted_edges = []
for u, v, b in edges:
weighted_edges.append((u, v, b + A[v]))
weighted_edges.append((v, u, b + A[u]))
return weighted_edges
if __name__=="__main__":
print(calculate_node_weight()) # [(1, 2, 13), (2, 1, 10), (2, 3, 10), (3, 2, 8), (1, 3, 13), (3, 1, 8)]
距離計算
sample.py
def final_distance_calculation():
A = [5, 3, 2, 4]
dist_from_dijkstra = [0, 8, 5, 10]
final_dist = [d + A[0] for d in dist_from_dijkstra]
return final_dist
print(final_distance_calculation()) # [5, 13, 10, 15]