LoginSignup
8
2
@nymwa(nymwa)

Kneser-NeyスムージングによるN-gram言語モデルを実装してミニマリズム言語トキポナを学習させる話

Last updated at Posted at 2022-06-02

最近ではニューラルネットを使った言語モデルがよく用いられていますが，N-gram言語モデルをいまさら実装し，いまどきKneser-Neyスムージングで遊んで知見を深めようという気持ちの記事です．せっかくなので，「Basic English」や「やさしい日本語」よりもかんたんで，単語が120語しかないミニマリズム言語トキポナの言語モデルを作成し，その挙動を観察します．

（この記事と同じ実装をgithubで公開しています　https://github.com/nymwa/knlm ）

N-gram 言語モデル

言語モデルとは，単語の列の出現確率を与える確率モデルです．単語列 $a_1, a_2, a_3, \cdots, a_n$ の確率を
$$p(a_1, a_2, a_3, \cdots, a_n)$$
として計算します．言語モデルは，「ことば」を確率で表したモデルと言うことができます．

言語モデルを用いて，単語列の確率を計算するとき，各単語ごとに確率を計算し，掛け合わせるということがよく行われます．この際，単語列の確率は，条件付き確率の積として表されます．

\begin{align*}
p(a_1, a_2, a_3, \cdots, a_n)
& = p(a_1) p(a_2, a_3, \cdots, a_n | a_1) (\because \text{確率の乗法定理}) \\
& = p(a_1) p(a_2 | a_1) p(a_3, \cdots, a_n | a_1, a_2) \\
& \vdots \\
& = \prod_{i = 1}^{n} p(a_i | a_1, \cdots, a_{i-1})
\end{align*}

N-gram 言語モデルは，上の式の条件付き確率の部分を，前に来る $N-1 $単語に限定して計算する言語モデルです．つまり，単語列 $a_{n-i+1}, \cdots, a_{i-1}$ を条件として，$a_i$を計算します．式にすると，
$$p(a_i | a_{i-N+1}, \cdots, a_{i-1})$$
となります．

2-gram 言語モデルだと直前の単語$a_i$のみを用いて
$$p(a_i | a_{i-1})$$
を計算し，長さ3の単語列 $a_1, a_2, a_3$ の確率は，
$$p(a_1) p(a_2 | a_1) p(a_3 | a_2)$$
と計算します．ただし，この際，単語列の開始と終了箇所に，特殊トークン<s>を置くことで，どこで開始し，どこで終了するかも確率として扱えるようにするのが，普通です．すると，
$$p(a_1, a_2, a_3) = p(a_1 | \text{<s>}) p(a_2 | a_1) p(a_3 | a_2) p(\text{<s>} | a_3)$$
という計算になります．

同様に，3-gram言語モデルの場合は，
$$p(a_1, a_2, a_3) = p(a_1 | \text{<s>}, \text{<s>}) p(a_2 | \text{<s>}, a_1) p(a_3 | a_1, a_2) p(\text{<s>} | a_3, a_2)$$
という計算になります．

Kneser-Ney スムージング

ゼロ頻度問題

N-gram言語モデルを用いて，単語列の確率を計算する場合，具体的にどのように計算すれば良いのでしょうか．

単に単語が現れる確率が多項分布に従っているということを仮定すると，単語 $b$ が単語列 $\boldsymbol{a} = a_1, a_2, \cdots, a_i$ の後に現れる確率は，学習データ中の単語列 $\boldsymbol{a}b$ の出現頻度を $C(\boldsymbol{a}b)$，単語列 $\boldsymbol{a}$ の直後に任意の単語が1つくる列の出現頻度を $C(\boldsymbol{a}\bullet)$ として，最尤推定により，
$$p(b|\boldsymbol{a}) = \frac{C(\boldsymbol{a}b)}{C(\boldsymbol{a}\bullet)}$$
として求められます．

しかし，この方法には問題があります．もしも，単語列 $\boldsymbol{a}x$ が学習コーパス中に一度も出現しない場合，$p(x|\boldsymbol{a}) = 0$となってしまうので，この確率の積により計算される単語列の確率も0と計算されてしまいます．出現頻度0というのは，その単語列は絶対に出現しないということを意味しますが，それは，偶然その学習データに出現しなかったということに過ぎず，別のデータにおいては出現する可能性もあります．

このような問題は，ゼロ頻度問題と呼ばれています．ゼロ頻度問題に対処するためには，なんらかの補正をかける方法を考える必要があります．この補正の方法にもいろいろあり，Kneser-Neyスムージングが提案されるまでの経緯もいろいろあるのですが，そういうのは全部なかったことにして，いきなり現れたものとして説明します．

割引法

ゼロ頻度問題に対処するために，頻度が1以上になっているN-gramの頻度を，そうじゃないN-gramに分けてあげるという考え方があります．この分けてあげる値のことを割引値といい，この方法を割引法といいます．また，このように学習データにないようなN-gramに対しても確率を割り当てる方法を，スムージング（平滑化）といいます．

割引法では，頻度から割引値 $D$ を引きます．なお，今後は，条件付き確率の条件の単語列を，$a\boldsymbol{b} = a, b_1, b_2, \cdots, b_i$ とします．
$$p(c|a\boldsymbol{b}) = \frac{C(a\boldsymbol{b}c)-D}{C(a\boldsymbol{b}\bullet)}$$
$D$ が引かれています．ただし，このままだと，$C(a\boldsymbol{b}c) = 0$のときに，確率が負を取ることになります．なので，必ず0以上になるようにします．
$$p(c|a\boldsymbol{b}) = \frac{\max(0, C(a\boldsymbol{b}c)-D)}{C(a\boldsymbol{b}\bullet)}$$
まだ問題があります．割引値$d$を他の単語列の確率に割り当てていないので，$\displaystyle\sum_{c\in V} p(c | a\boldsymbol{b}) < 1$ となってしまいます．N-gramでは頻度が0だった列にも確率を割り当てたいので，割り引かれた分の確率は，N-1gram確率の値 $p(c|\boldsymbol{b})$ に従って割り当てたいと思います．
$$p(c|a\boldsymbol{b}) = \frac{\max(0, C(a\boldsymbol{b}c)-D)}{C(a\boldsymbol{b}\bullet)} + \gamma p(c|\boldsymbol{b})$$
ここで，$\gamma$は正規化のための係数です．

こうすることで，無事ゼロ頻度問題を解決できます．ただ，$\gamma$をどう定義すればいいのでしょうか．

Kneser-Ney スムージング

Kneser-Neyスムージングを行ったN-gram言語モデルは次の式のようになります．

\begin{align*}
p_\text{最高次}(c | a \boldsymbol{b}) 
&=
\begin{cases}
\cfrac{
\max(0, C(a \boldsymbol{b} c) - D)
}{
C(a \boldsymbol{b} \bullet)
}
+
\cfrac{
D U(a \boldsymbol{b} \bullet)
}{
C(a \boldsymbol{b} \bullet)
}
p_\text{低次}(c | \boldsymbol{b})
& C(a \boldsymbol{b} \bullet) > 0 \text{のとき}
\\
p_\text{低次}(c | \boldsymbol{b})
& C(a \boldsymbol{b} \bullet) = 0 \text{のとき}
\end{cases}
\\

p_\text{低次}(c | a \boldsymbol{b})
&=
\begin{cases}
\cfrac{
\max(0, U(\bullet a \boldsymbol{b} c) - D)
}{
U(\bullet a \boldsymbol{b} \bullet)
}
+
\cfrac{
D R(\bullet a \boldsymbol{b} \bullet)
}{
U(\bullet a \boldsymbol{b} \bullet)
}
p_\text{低次}(c | \boldsymbol{b})
& U(\bullet a \boldsymbol{b} \bullet) > 0 \text{のとき}
\\
p_\text{低次}(c | \boldsymbol{b})
& U(\bullet a \boldsymbol{b} \bullet) = 0 \text{のとき}
\end{cases}
\\

p_\text{低次}(\varepsilon)
&=
\frac{1}{|V|}\ \ \ \ \ (\text{※ $V$は語彙(=単語の集合)})
\end{align*}

わけがわからないので，ひとつずつ説明します．

まず，Kneser-Neyスムージングは，割引法から派生した手法です．$\gamma$の部分が，$\frac{DU}{C}$みたいなやつになっています．割引法と違う点として，$p_\text{最高次}, p_\text{低次}$ の2つの確率があります．例えば，5-gram言語モデルであれば，5-gramの入力，つまり，$|a\boldsymbol{b}c| = 5$ のときだけ，$p_\text{最高次}$を計算し，それより下の，4-gram, 3-gramの入力には，$p_\text{低次}$を計算します．最初の次元とそれ以降で挙動を変えることで，性能がよくなるんですが，なんでそうなるかとかまでは説明しないので，気になるひとは調べてください．説明の中に "San Francisco" とか "Ronald Reagan" がでてきたら，多分それです．

$C(a \boldsymbol{b} c)$は，単純に単語列$a \boldsymbol{b} c$の出現頻度です．$C(a \boldsymbol{b} \bullet)$は，単語列$a \boldsymbol{b}$に，さらに1単語続くものの出現頻度です．$\displaystyle\sum_{z \in V} C(a \boldsymbol{b} z)$ と同じです．

$U(a \boldsymbol{b} \bullet)$は，$a \boldsymbol{b} z$ となるような $z$ の種類数で，$| \lbrace z | C(a \boldsymbol{b} z) > 0 \rbrace |$と書けます．異なり数と呼ばれます．また，$U(a \boldsymbol{b} \bullet) \leq |V|$ です．$U(\bullet a \boldsymbol{b} \bullet)$とある場合は，$z a \boldsymbol{b} w$ となるような組$(z, w)$の種類数で，$| \lbrace (z, w) | C(z a \boldsymbol{b} w) > 0 \rbrace |$ を意味します．$U(\bullet a \boldsymbol{b} \bullet) \leq |V|^2$ です．

$R(\bullet a \boldsymbol{b} \bullet)$は，すこし特殊で，$\text{(任意の単語)} + a + \boldsymbol{b} + z$ となる $z$ の種類です． $| \lbrace z | U(\bullet a \boldsymbol{b} z ) > 0 \rbrace |$ と書けます．$R(\bullet a \boldsymbol{b} \bullet) \leq |V|$ です．

式中の項の分母が0になるような場合は，そのまま1つ下の次数の計算結果を，この次数での計算結果としています．

$D$ の値は定数でよくて，0.75 が用いられることが多いです．"Good-Turing 0.75"とかで検索すると出てくると思います．$0 < D < 1$ です．

具体的に，Kneser-Neyスムージングを用いた5-gram言語モデルの式を書いてみます．

\begin{align*}
p_0 (\varepsilon)

&=

\frac{1}{|V|} 

\\

p_1 (e)
&=
\frac{
\max(0, U(\bullet e) - D)
}{
U(\bullet \bullet)
}
+
\frac{
DR(\bullet \bullet)
}{
U(\bullet \bullet)
}
p_0(\varepsilon)

\\

p_2 (e | d)
&=
\frac{
\max(0, U(\bullet de) - D)
}{
U(\bullet d \bullet)
}
+
\frac{
DR(\bullet d \bullet)
}{
U(\bullet d \bullet)
}
p_1(e)

\\

p_3 (e | cd)
&=
\frac{
\max(0, U(\bullet cde) - D)
}{
U(\bullet cd \bullet)
}
+
\frac{
DR(\bullet cd \bullet)
}{
U(\bullet cd \bullet)
}
p_2(e | d)

\\

p_4 (e | bcd)
&=
\frac{
\max(0, U(\bullet bcde) - D)
}{
U(\bullet bcd \bullet)
}
+
\frac{
DR(\bullet bcd \bullet)
}{
U(\bullet bcd \bullet)
}
p_3(e | cd)

\\
p_5 (e | abcd)
&=
\frac{
\max(0, C(abcde) - D)
}{
C(abcd \bullet)
}
+
\frac{
DU(abcd \bullet)
}{
C(abcd \bullet)
}
p_4(e | bcd)

\end{align*}

$p_1(e) = \frac{U(\bullet e)}{U(\bullet \bullet)}$ としても同じということもわかりますが，$p_0(\varepsilon) = \frac{1}{|V|}$ から計算を始めた方がプログラムがかんたんになります．

式を見てもわからないがちですが，実装を見ると割とわかりがちです．

実装

まず，学習をするコードです．

c_abcやu_xbcなどが，$C(a\boldsymbol{b}c)$や$U(\bullet\boldsymbol{b}c)$に対応していて，その頻度を数え上げています．

import json
from argparse import ArgumentParser
from collections import defaultdict

class Trainer:

    def __init__(self, n):
        self.n = n
        self.eos = '<s>'
        self.c_abc = defaultdict(int) # C(abc)
        self.c_abx = defaultdict(int) # C(ab・)
        self.u_abx = defaultdict(int) # U(ab・)
        self.u_xbc = defaultdict(int) # U(・bc)
        self.u_xbx = defaultdict(int) # U(・b・)
        self.s_xbx = defaultdict(set) # R(・b・)を求めるために"*b・"となるような・の集合を持つ辞書

    def count_ngram(self, ngram): # n-gram に対して count
        assert len(ngram) >= 2 # 1-gramだと，ab, bc, b, cが求められない

        abc = '|'.join(ngram)
        ab = '|'.join(ngram[:-1])
        bc = '|'.join(ngram[1:])
        b = '|'.join(ngram[1:-1])
        c = ngram[-1]

        self.c_abc[abc] += 1
        self.c_abx[ab] += 1
        if self.c_abc[abc] == 1: # 初めて現れたn-gram abcに対して，U(...)を更新
            self.u_abx[ab] += 1
            self.u_xbc[bc] += 1
            self.u_xbx[b] += 1
        self.s_xbx[b] = self.s_xbx[b] | {c}

    def count_sent_ngram(self, n, sent): # 文 sent 中の n-gram について count する
        sent = [self.eos] * (n - 1) + sent + [self.eos]
        ngram_iter = zip(*[sent[i:] for i in range(n)])
        for ngram in ngram_iter:
            self.count_ngram(ngram)

    def count_sent(self, sent): # 文を受け取って n-gram を数えていく
        for n in range(2, self.n + 1): # 2-gramからN-gramまでで数える, 式を見ればわかるが，1-gramは使わない
            self.count_sent_ngram(n, sent)

    def make_vocab(self): # 語彙のリストを作る
        vocab = [
            (key, value)
            for key, value
            in self.c_abx.items()
            if len(key.split('|')) == 1]
        vocab.sort(key = lambda x: -x[1]) # 頻度でソートしている
        vocab = [token for token, freq in vocab]
        return vocab

    def to_json(self): # 結果を json として保存する
        r_xbx = {key: len(value) for key, value in self.s_xbx.items()} # s_xbxをR(・b・)に変換する
        dct = {
            'n': self.n,
            'eos': self.eos,
            'c_abc': dict(self.c_abc),
            'c_abx': dict(self.c_abx),
            'u_abx': dict(self.u_abx),
            'u_xbc': dict(self.u_xbc),
            'u_xbx': dict(self.u_xbx),
            'r_xbx': r_xbx,
            'vocab': self.make_vocab()}
        js = json.dumps(dct, indent = 4)
        return js


def parse_args():
    parser = ArgumentParser()
    parser.add_argument('--n', type = int, default = 5)
    parser.add_argument('--train', default = 'train.txt')
    parser.add_argument('--lm', default = 'lm.json')
    return parser.parse_args()


def main():
    args = parse_args()

    trainer = Trainer(args.n)

    with open(args.train) as f:
        for line in f:
            sent = line.strip().split()
            trainer.count_sent(sent) # 文の単語のリストを数えていく

    with open(args.lm, 'w') as f:
        print(trainer.to_json(), file = f) # 保存する


if __name__ == '__main__':
    main()

このコードを実行すると，lm.jsonとかいう大きいファイルができて，5-gram言語モデルができます．

Kneser-Neyスムージングを用いる言語モデルは次のように実装できます．最高次(predict)と低次で(predict_lower)で式が別れていて，LM(...).predict(ngram)とすると，N-gramの確率を予測してくれます．

import json

class LM:

    def __init__(self, path, d):
        with open(path) as f:
            dct = json.load(f) # 読み込み
        self.n = dct['n']
        self.eos = dct['eos']
        self.c_abc = dct['c_abc']
        self.c_abx = dct['c_abx']
        self.u_abx = dct['u_abx']
        self.u_xbc = dct['u_xbc']
        self.u_xbx = dct['u_xbx']
        self.r_xbx = dct['r_xbx']
        self.vocab = dct['vocab']
        self.d = d # 割引値D

    def predict_lower(self, ngram): # 低次の確率を求める
        if len(ngram) == 0:
            return 1 / len(self.vocab) # p(ε)

        abc, ab = '|'.join(ngram), '|'.join(ngram[:-1])

        # 第1項
        if (abc in self.u_xbc) and (ab in self.u_xbx):
            alpha = (self.u_xbc[abc] - self.d) / self.u_xbx[ab]
        else:
            alpha = 0 # maxで0が選ばれる

        # 第2項
        if ab in self.u_xbx:
            gamma = self.d * self.r_xbx[ab] / self.u_xbx[ab]
        else:
            gamma = 1 # そのまま1つ下の次元の値を使う

        return alpha + gamma * self.predict_lower(ngram[1:]) # 再帰呼出し

    def predict(self, ngram): # 最高次の確率を求める
        abc, ab = '|'.join(ngram), '|'.join(ngram[:-1])

        # 第1項
        if (abc in self.c_abc) and (ab in self.c_abx):
            alpha = (self.c_abc[abc] - self.d) / self.c_abx[ab]
        else:
            alpha = 0 # maxで0が選ばれる

        # 第2項
        if ab in self.c_abx:
            gamma = self.d * self.u_abx[ab] / self.c_abx[ab]
        else:
            gamma = 1 # そのまま1つ下の次元の値を使う

        return alpha + gamma * self.predict_lower(ngram[1:]) # n-1次以降は predict_lower

これで言語モデルが作れるようになりました．1つ別の話をしてから，実際に学習を行います．

Kneser-Neyスムージングで推定された値って確率になっているの？

言語モデルは確率を与えるモデルなので，標本空間全体だと確率の和が1になっていないといけません．つまり，
$$\sum_{c \in V} p(c | a \boldsymbol{b}) = 1$$
を満たしている必要があります．

Kneser-Neyスムージングの式も，当然これを満たしています（どちらかというと，これを満たすように$U$や$R$を定めていると言ったほうがよいです）．式を見てその事実にすぐ気づく人も，世の中にはそこそこいるらしいですが，自分は最初にKneser-Neyスムージングを知ってからそのことが理解できるまで，3年近くかかってしまったし，割と自明じゃないので，ここで説明します．

まず，示したいことは，次のことです．
$$\sum_{c \in V} p_\text{最高次} (c | a \boldsymbol{b}) = 1$$
これを，以下の順に示していきます．

  1. $\sum_{c \in V} p_\text{低次} (\varepsilon) = 1$ を示す．
  2. $\sum_{c \in V} p_\text{低次} (c | \boldsymbol{b}) = 1 \implies \sum_{c \in V} p_\text{低次} (c | a \boldsymbol{b}) = 1$
  3. $\sum_{c \in V} p_\text{低次} (c | \boldsymbol{b}) = 1 \implies \sum_{c \in V} p_\text{最高次} (c | a \boldsymbol{b}) = 1$
    ただし，$0 < D < 1$ です．

以上の1, 2, 3が正しければ，1, 2で，数学的帰納法より，任意の次元で$p_\text{低次}$の和が1になり，そのことと3より，$p_\text{最高次}$の和も1となることがわかります．

1の証明

$$\sum_{c \in V} p_\text{低次} (\varepsilon) = \sum_{c \in V} \frac{1}{|V|} = |V| \frac{1}{|V|} = 1$$

2の証明

$\max (0, U(\bullet a \boldsymbol{b} c) - D)$について，$0 < D < 1$ ならば，$\max$の中の0ではなくて，$U(\bullet a \boldsymbol{b} c) - D$ が選ばれるのは，$U(\bullet a \boldsymbol{b} c) > 0$となるときです．そのような$c$の数は，
$$R(\bullet a \boldsymbol{b} \bullet) = |\lbrace c | U(\bullet a \boldsymbol{b} c) > 0 \rbrace |$$
です．よって，

\begin{eqnarray*}
& &
\sum_{c \in V}
\frac{\max(0, U(\bullet a \boldsymbol{b} c ) - D)}{U(\bullet a \boldsymbol{b} \bullet)} \\
&=&
\frac{
\sum_{c \in \lbrace c | U(\bullet a \boldsymbol{b} c) > 0 \rbrace} U(\bullet a \boldsymbol{b} c)
}{
U(\bullet a \boldsymbol{b} \bullet)}-
R(\bullet a \boldsymbol{b} \bullet)
\frac{
D
}{
U(\bullet a \boldsymbol{b} \bullet)}
\\
&=&\frac{U(\bullet a \boldsymbol{b} \bullet)}{U(\bullet a \boldsymbol{b} \bullet)}-
\frac{
DR(\bullet a \boldsymbol{b} \bullet)
}{
U(\bullet a \boldsymbol{b} \bullet)}
\\
&=&1-
\frac{
DR(\bullet a \boldsymbol{b} \bullet)
}{
U(\bullet a \boldsymbol{b} \bullet)}
\end{eqnarray*}

となります．これを使うと，2が示せます．

\begin{eqnarray*}
& &
\sum_{c \in V}
p_\text{低次}
(c | a \boldsymbol{b})
\\
&=&
\sum_{c \in V}
\frac{
\max(0, U(\bullet a \boldsymbol{b} c) - D)
}{
U(\bullet a \boldsymbol{b} \bullet)}
+
\sum_{c \in V}
\frac{
D R(\bullet a \boldsymbol{b} \bullet)
}{
U(\bullet a \boldsymbol{b} \bullet)}
p_\text{低次}
(c | \boldsymbol{b})
\\
&=&1-
\frac{
DR(\bullet a \boldsymbol{b} \bullet)
}{
U(\bullet a \boldsymbol{b} \bullet)}
+
\sum_{c \in V}
\frac{
D R(\bullet a \boldsymbol{b} \bullet)
}{
U(\bullet a \boldsymbol{b} \bullet)}
p_\text{低次}
(c | \boldsymbol{b})
\\
&=&1-
\frac{
DR(\bullet a \boldsymbol{b} \bullet)
}{
U(\bullet a \boldsymbol{b} \bullet)}
+
\frac{
D R(\bullet a \boldsymbol{b} \bullet)
}{
U(\bullet a \boldsymbol{b} \bullet)}
\underbrace{
\sum_{c \in V}
p_\text{低次}
(c | \boldsymbol{b})
}_{=1}
\\
&=&1-
\frac{
DR(\bullet a \boldsymbol{b} \bullet)
}{
U(\bullet a \boldsymbol{b} \bullet)}
+
\frac{
D R(\bullet a \boldsymbol{b} \bullet)
}{
U(\bullet a \boldsymbol{b} \bullet)}
\\
&=&1
\end{eqnarray*}

よって，$$\sum_{c \in V} p_\text{低次} (c | \boldsymbol{b}) = 1 \implies \sum_{c \in V} p_\text{低次} (c | a \boldsymbol{b}) = 1$$ です．

3の証明

2と同様に示せます．

$\max (0, C(a \boldsymbol{b} c) - D)$について，$0 < D < 1$ ならば，$\max$の中の0ではなくて，$C(a \boldsymbol{b} c) - D$ が選ばれるのは，$C(a \boldsymbol{b} c) > 0$となるときです．そのような$c$の数は，
$$U(a \boldsymbol{b} \bullet) = |\lbrace c | C(a \boldsymbol{b} c) > 0 \rbrace |$$
です．よって，

\begin{eqnarray*}
& &
\sum_{c \in V}
\frac{\max(0, C(a \boldsymbol{b} c ) - D)}{C(a \boldsymbol{b} \bullet)} \\
&=&
\frac{
\sum_{c \in \lbrace c | C(a \boldsymbol{b} c) > 0 \rbrace} C(a \boldsymbol{b} c)
}{
C(a \boldsymbol{b} \bullet)}-
U(a \boldsymbol{b} \bullet)
\frac{
D
}{
C(a \boldsymbol{b} \bullet)}
\\
&=&
\frac{
C(a \boldsymbol{b} \bullet)
}{
C(a \boldsymbol{b} \bullet)}-
\frac{
DU(a \boldsymbol{b} \bullet)
}{
C(a \boldsymbol{b} \bullet)}
\\
&=&1-
\frac{
DU(a \boldsymbol{b} \bullet)
}{
C(a \boldsymbol{b} \bullet)}
\\
\end{eqnarray*}

となります．これを使うと，3が示せます．

\begin{eqnarray*}
& &
\sum_{c \in V}
p_\text{最高次}
(c | a \boldsymbol{b})
\\
&=&
\sum_{c \in V}
\frac{
\max(0, C(a \boldsymbol{b} c) - D)
}{
C(a \boldsymbol{b} \bullet)
}
+
\sum_{c \in V}
\frac{
D U( \boldsymbol{b} \bullet)
}{
C(a \boldsymbol{b} \bullet)
}
p_\text{低次}
(c | \boldsymbol{b})
\\
&=&1-
\frac{
DU(a \boldsymbol{b} \bullet)
}{
C(a \boldsymbol{b} \bullet)
}
+
\sum_{c \in V}
\frac{
D U(a \boldsymbol{b} \bullet)
}{
C(a \boldsymbol{b} \bullet)}
p_\text{低次}
(c | \boldsymbol{b})
\\
&=&1-
\frac{
D U(a \boldsymbol{b} \bullet)
}{
C(a \boldsymbol{b} \bullet)}
+
\frac{
D U(a \boldsymbol{b} \bullet)
}{
C(a \boldsymbol{b} \bullet)
}
\underbrace{
\sum_{c \in V}
p_\text{低次}
(c | \boldsymbol{b})
}_{=1}
\\
&=&1-
\frac{
D U(a \boldsymbol{b} \bullet)
}{
C(a \boldsymbol{b} \bullet)
}
+
\frac{
D U(a \boldsymbol{b} \bullet)
}{
C(a \boldsymbol{b} \bullet)
}
\\
&=&1

\end{eqnarray*}

よって，$$\sum_{c \in V} p_\text{低次} (c | \boldsymbol{b}) = 1 \implies \sum_{c \in V} p_\text{最高次} (c | a \boldsymbol{b}) = 1$$ です．

以上のことより，Kneser-Neyスムージングで出てくる値が，ちゃんと次の単語が起こる確率になっていることがわかりました．

トキポナとは

ミニマリズム人工言語です．120語の単語を覚えて，かんたんな文法を覚えるだけで，非常に多くのことが表現できます．できるひとなら数時間あればできるようになります．

120語のリストは，以下のようになっています．

次の動画を見れば，概要がわかります．

トキポナの文法をまとめたスライドとしては，次のツイートのものがとても良くできています．

（追記(2023/05/15): もとのツイートをしているアカウントが鍵アカになってしまったので、同じスライドのリンクを掲載します。）
https://github.com/notolyte/tokipona_bunpou/blob/main/tokipona_grammar.pdf

1ページにまとまった単語リストは https://github.com/nymwa/new-toki-pona-word-list/blob/main/words.pdf が便利です．

トキポナは，「Basic English」や「やさしい日本語」よりも，さらにかんたんな言語と言えると思います．自然言語は語彙が多く，小規模なデータセットでかんたんに計算機応用を試せるデータセットがあまりないような気がします．画像処理では，MNISTなどの使い勝手のいいデータセットがありますが，トキポナで作成したデータセットはそれと同程度の規模感なため，トキポナであれば，よりかんたんに言語処理を試すことができるかもしれないと思っています．

トキポナN-gram言語モデルを学習してハイパーパラメータ探索

トキポナのコーパスを使って，実際にN-gram言語モデルを学習してみます．訓練データには，tatoeba.org のデータを用います（tatoeba.org/ja/downloads）．訓練データには，自前で集めた他のデータも追加して，全部で，51,265文，592,591語です．

開発用のデータとして，A Formal Grammar for Toki Ponaにある100文と，トキポナ公式本にある300文の合わせて，400文，3090語を用います．

トークナイズは単語単位で行います．トキポナのトークナイザ ilonimiを用います．固有名詞は<proper>，数字は<number>，未知語は<unk>に置き換えます．

Kneser-Neyスムージングには，割引値$D$というハイパーパラメータがありました．これが一体，$0<d<1$ の間でどこが良いのかを調べます．

# 言語モデル
lm = LM('lm.json', d = 0.75)

# 開発データ
with open('valid.txt') as f:
    data = [line.strip().split() for line in f]

# 文を N-gram の列に変換します
def sent_to_ngrams(lm, sent):
    sent = ['<s>'] * (lm.n - 1) + sent + ['<s>']
    ngram_iter = zip(*[sent[i:] for i in range(lm.n)])
    return list(ngram_iter)

# 言語モデルの評価指標 perplexity を計算します
def calc_ppl(lm, data, d):
    lm.d = d
    probs = [
        -np.log2(lm.predict(ngram))
        for sent in data
        for ngram in sent_to_ngrams(lm, sent)]
    return 2 ** np.mean(probs)

# perplexityを計算して，pyplotでグラフを描画します
xs = np.linspace(0, 1, 101)[1:]
ys = [calc_ppl(lm, data, d) for d in xs]
plt.figure(dpi = 100)
plt.plot(xs, ys)
plt.xlabel('D')
plt.ylabel('perplexity')
plt.show()

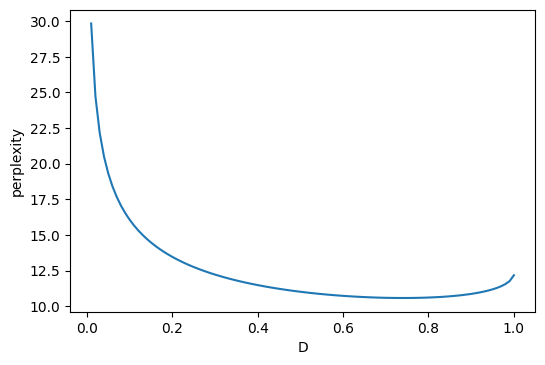
$D$を変えながら，perplexityを計測します．perplexityが低いほど，言語モデルの性能は良いと言えます．

次の図に結果を示します．$D = 0.74$が一番良く，このとき，perplexityが10.58となっています．

ppl.png

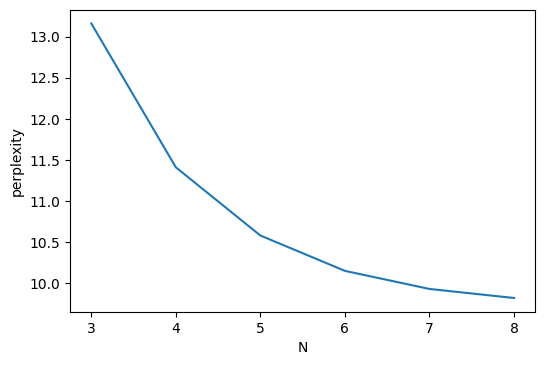
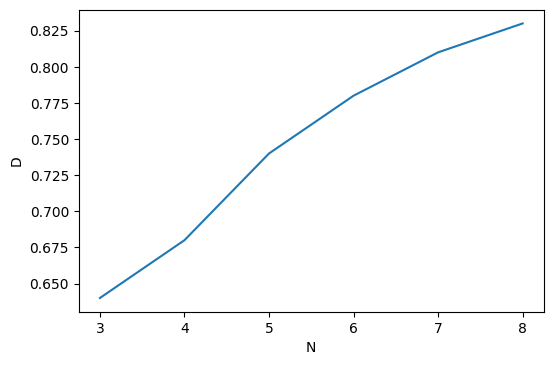
ちなみに，N-gramのNの値を3~8まで変えて，perplexityを計測してみました．Nを変えたときの，perplexityと，最も良かったときの$D$のグラフを載せます．

Nが8程度までであれば，Nの値が大きいほど，性能が高くなり，割引値も大きくなるようです．

ppl2.png
d.png

ちなみに，$h=512$の2層のLSTMの言語モデルを学習すると，perplexity = 10.55となりました．Kneser-Ney言語モデルとニューラル言語モデルで性能に差がないという結果になってしまいましたが，長い文脈などを捉えるためには，ニューラルネットのほうが適しているかもしれません．

ランダムな文生成

せっかく言語モデルを作ったので，ランダムな文生成を行います．

lm.d = 0.74 # 先程のDを使う
for _ in range(10): # 10回生成
    sent = ['<s>'] * 4
    for i in range(30):
        probs = [lm.predict(sent[-4:] + [token]) for token in lm.vocab] # 次の単語の確率を計算
        token = np.random.choice(lm.vocab, p = probs) # 重み付けしてランダムに選択
        if token != '<s>':
            sent.append(token)
        else:
            break
    print(' '.join(sent[4:]))

生成した結果は次のようになります．訳も載せれるところは載せました．

wawa ona li weka ala e tenpo en ma lili mute tawa mi anu seme ? # （非文，enは目的語中で用いない）
tenpo ni li pini . # 今が終わる．
jan <proper> li ante mute e sewi tomo loje li lukin e ma kasi pi pona uta , la ni li pona tawa mi . # （文法的に正しいが意味がわからない）
tenpo seme la mi lon tawa sina ? # あなたにとって私が正しいのはどんな時か？
sina jo ala jo e ma tomo pi pona sijelo li toki e sona len mute . # （非文，前半は疑問文だが，疑問符で終わっていない）
mi mute li toki . # 私達は話す．
mije ni li jan pi kama sona . # この男は学生だ．
tenpo pi suli seme la pilin mi la ona li pona mute tawa sina : sina tawa lon poka mi lon poka pi ijo ni . # （非文，laは1文中に1度しか用いない）
ona li jo ala jo e pan ? # 彼は食べるものを持っていますか？
mi kama sona e ijo sin . # 私は新しいことを学ぶ．

短い文は意味が通るようですが，長い文で意味が通りかつ文法的な文を生成するのは難しいようです．また，前半の文脈が後半に効いてない事例もあります．N-gram言語モデルでは，N単語後ろまでしか遡れないため，このようなことがおきます．このようなことを避けたい場合は，ニューラルネットのほうが適している可能性があります．

ただ，ニューラルネットを使って日頃から言語処理をしている人（今の私）ではなくて，人工言語を架空世界創作などと結びつけて使っている人（私の周りに多いがち）の場合は，ニューラル言語モデルよりもN-gram言語モデルの方が使い勝手が良く，応用しやすいということも考えられます．性能の良さだけじゃなくて，計算機環境や使いやすさというのが大事になる場所もあります．日頃スパコンぐわんぐわん回してる人は世界のごく少数です．

エントロピーを観察する

これは，今年(2022年)の言語処理学会年次大会で『創発言語でもHarrisの分節原理は成り立つのか？』というのがあったので，トキポナでも成り立つのか気になってやってみたものです．

左から右に単語を生成する言語モデルと，右から左に単語を生成する言語モデルを作成し，各単語のエントロピーを求めて，その変化をグラフにします．両方の言語モデルによるエントロピーの和も描きました．

lml = LM('lm.json', d = 0.75)
lmr = LM('lm.rev.json', d = 0.75)

def entropy(lm, ngram):
    probs = np.array([lm.predict(list(ngram) + [token]) for token in lm.vocab])
    probs = probs / probs.sum()
    ents = [p * np.log(p) for p in probs]
    return -np.sum(ents)

for sent in data[:30]:
    cappedl = ['<s>'] * 4 + sent
    cappedr = ['<s>'] * 4 + sent[::-1]
    
    ngram_listl = list(zip(*[cappedl[i:] for i in range(4)]))
    ngram_listr = list(zip(*[cappedr[i:] for i in range(4)]))
    
    entsl = [entropy(lml, ngram) for ngram in ngram_listl][:-1]
    entsr = [entropy(lmr, ngram) for ngram in ngram_listr][:-1][::-1]
    ents = [l + r for l, r in zip(entsl, entsr)]
    
    plt.figure(dpi=100)
    plt.plot(ents)
    plt.plot(entsl)
    plt.plot(entsr)
    plt.legend(['L↔R', 'L→R', 'L←R'])
    for index, (ent, token) in enumerate(zip(ents, sent)):
        plt.annotate(token, (index, ent + 0.1), size=16)
    plt.show()

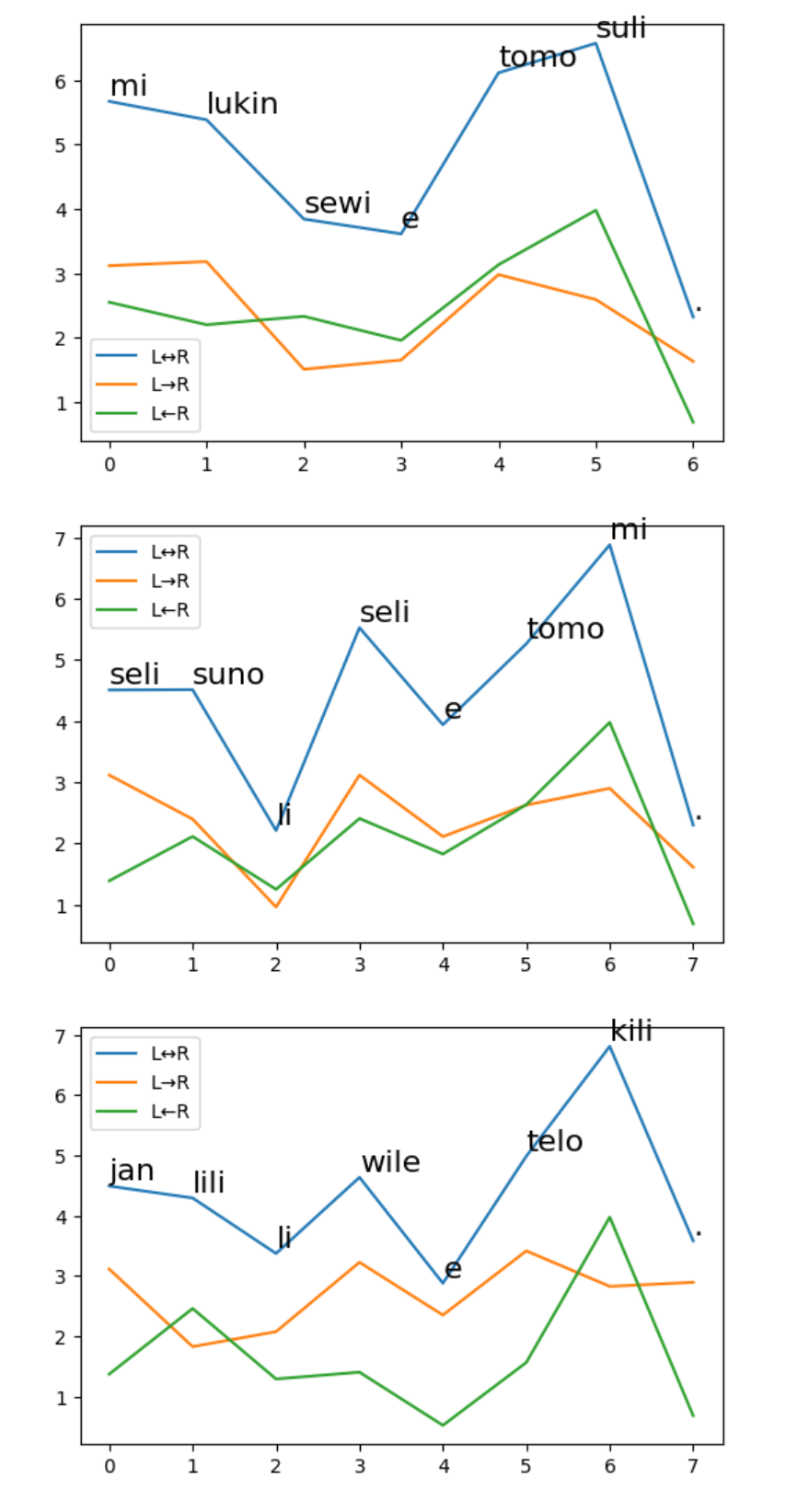
実際の図は下にしめしたようなものになります．Harrisの分節原理は，教師なし単語分割に使えるという話ですが，トキポナでは単語にもう分割されているので，チャンキングみたいなことができないかなあと思ったのですが，そんなことは当然できませんでした．

ただ，liやeなどの機能語でエントロピーが下がっていたりして，ある程度はチャンキングのようなことも可能な気がします．左→右のモデルと右→左のモデルでエントロピーが大きく異なる場所も多く，そういう場所での挙動がどうなっているのかというのを，トキポナだけでなく，日本語や英語でもいろいろと考えると，もしかしたら面白い知見が得られるかもしれません．

おわり

8
2
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
8
2