Kaggle の入り口 "Titanic"
これまで存在は知りつつも、なかなかチャレンジできずにいたKaggleでしたが、意を決してチャレンジしてみることにしました。
まずは、Kaggleの入り口とでもいうべきチュートリアルのコンペティション "Titanic"から始めてみようと思います。
"Titanic" はどういう問題なのか?
20世紀初頭のタイタニック号沈没事件の乗客名簿(乗客の属性)をもとに、その乗客の生還/死亡を推定するコンペティションです。
データは、訓練データ(乗客の属性+生還/死亡情報)とテストデータ(乗客の属性のみ、生還/死亡情報なし)を与えられます。
訓練データで機械学習を行い、その結果を用いて、テストデータの乗客の生還/死亡を推定するのです。
生還/死亡の推定精度が高い(=よりたくさんの乗客について、生死を正しく当てた)ほど、コンペで上位になれます。
訓練データの内容
| 変数名 | 定義 | 備考(値域など) | 学習に使用/未使用 |
|---|---|---|---|
| Survival | 生還/死亡 | 0:死亡, 1:生還 | 使用 |
| Pclass | 客室クラス | 1 = 1st, 2 = 2nd, 3 = 3rd(小さいほど良いクラス) | 使用 |
| Name | 名前 | 未使用 | |
| Sex | 性別 | 使用 | |
| Age | 年齢 | 使用 | |
| Sibsp | 兄弟(義兄弟含む)あるいは配偶者で同乗している人数 | 使用 | |
| Parch | 親あるいは子で同乗している人数 | 使用 | |
| Ticket | チケット番号 | 未使用 | |
| Fare | Passenger fare | 使用 | |
| Cabin | 客室番号 | 未使用 | |
| Embarked | 乗船した港 | C = Cherbourg, Q = Queenstown, S = Southampton | 使用 |
「チケット番号」「客室番号」は、予測に寄与すると思い難いので学習には使用していません。
「名前」は、今回学習に使用しませんでしたが、もしかするとこれを使うことで若干予測精度を上げることができるのかもしれません。「同じ姓は家族である可能性が高い」「同じ家族で~という属性は助かり、~という属性は助からない傾向にある(たとえば、Ageの大きい家族(親)はAgeの小さい家族(子)を優先して助ける、など)」予測に寄与する可能性があります。次回以降の課題としたいと思います。
ライブラリのインポート+データの取り込み
まずは、各種ライブラリのインポートとデータの取り込みを行います。
データの取り込みは、pandasのread_csvメソッドを使用します。
# データの前処理につかうライブラリ
import pandas as pd
from pandas import DataFrame
import matplotlib.pyplot as plt
import numpy as np
# 学習につかうライブラリ
from sklearn.preprocessing import LabelEncoder, OneHotEncoder, Imputer, StandardScaler
from sklearn import linear_model, cross_validation, tree
from sklearn.svm import SVC
from sklearn.neural_network import MLPClassifier
from sklearn.model_selection import learning_curve
# 訓練データ取り込み
df_train = pd.read_csv('train.csv')
# テストデータ取り込み
df_test = pd.read_csv('test.csv')
先頭5行を表示して、取り込んだ訓練データの内容がどんなものであるか確認します。
df_train.head(5)
| PassengerId | Survived | Pclass | Name | Sex | Age | SibSp | Parch | Ticket | Fare | Cabin | Embarked | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 3 | Braund, Mr. Owen Harris | male | 22.0 | 1 | 0 | A/5 21171 | 7.2500 | NaN | S |
| 1 | 2 | 1 | 1 | Cumings, Mrs. John Bradley (Florence Briggs Th... | female | 38.0 | 1 | 0 | PC 17599 | 71.2833 | C85 | C |
| 2 | 3 | 1 | 3 | Heikkinen, Miss. Laina | female | 26.0 | 0 | 0 | STON/O2. 3101282 | 7.9250 | NaN | S |
| 3 | 4 | 1 | 1 | Futrelle, Mrs. Jacques Heath (Lily May Peel) | female | 35.0 | 1 | 0 | 113803 | 53.1000 | C123 | S |
| 4 | 5 | 0 | 3 | Allen, Mr. William Henry | male | 35.0 | 0 | 0 | 373450 | 8.0500 | NaN | S |
前処理(データの整形)
取り込んだデータは、以下のような値を含んで入りため、そのままでは機械学習モデルに適用できません。
- 非数値データ(文字列で表現されたカテゴリカルデータ)
- 欠損値(NaN)
そこで、以下のようなものを利用して、前処理(データの整形を行います)
- LabelEncoder
- カテゴリカルデータを数値に変換するモジュールです。たとえば、性別であれば、男性には 0 を割り当て、女性には 1 を割り当てる、という具合です
。
- カテゴリカルデータを数値に変換するモジュールです。たとえば、性別であれば、男性には 0 を割り当て、女性には 1 を割り当てる、という具合です
- OneHotEncoder
- LabelEncoder で出力すると、各カテゴリに 0, 1, 2, ... という数字を割り当てますが、これは勝手に付与されたラベルであり、ほとんどの場合、大小関係に意味はありません。しかし、機械学習の中でこの大小関係に意味を見出そうてして、予測精度に悪影響をおよぼす可能性があります。これを防ぐために、「ダミー変数化」という操作をするモジュールです。
- Imputer
- 欠損値の補完を行うモジュール。より簡易的には、DataFrame.fillnaメソッドを使ったりもします。
以下に前処理のコードを記載します。
学習モデルに渡すデータ = transform_data(ファイルから取り込んだデータ)
という形で使用します。
# Sex
lb_enc_sex = LabelEncoder()
lb_sex = lb_enc_sex.fit_transform(df_train['Sex'])
oh_enc_sex = OneHotEncoder()
oh_enc_sex.fit(np.array(lb_sex).reshape(-1,1))
# Age
imp_age = Imputer(missing_values='NaN', strategy='mean', axis=0, verbose=0, copy=True)
imp_age.fit(np.array(df_train['Age']).reshape(-1, 1))
# Fare
imp_fare = Imputer(missing_values='NaN', strategy='mean', axis=0, verbose=0, copy=True)
imp_fare.fit(np.array(df_train['Fare']).reshape(-1, 1))
# Embarked
df_train['Embarked'] = df_train['Embarked'].fillna('U')
lb_enc_emb = LabelEncoder()
lb_emb = lb_enc_emb.fit_transform(df_train['Embarked'])
oh_enc_emb = OneHotEncoder()
oh_enc_emb.fit(np.array(lb_emb).reshape(-1,1))
def transform_data(df):
# Sex
lb_sex = lb_enc_sex.transform(df['Sex'])
enc_sex = oh_enc_sex.transform(np.array(lb_sex).reshape(-1,1))
df_sex = DataFrame(enc_sex.toarray(), columns=['male', 'female'])
# Age
age = imp_age.transform(np.array(df['Age']).reshape(-1, 1))
df_age = DataFrame(age, columns=['Age'])
# Fare
fare = imp_fare.transform(np.array(df['Fare']).reshape(-1, 1))
df_fare = DataFrame(fare, columns=['Fare'])
# Embarked
lb_emb = lb_enc_emb.transform(df['Embarked'])
enc_emb = oh_enc_emb.transform(np.array(lb_emb).reshape(-1,1))
df_emb = DataFrame(enc_emb.toarray(), columns=['C', 'Q', 'S', 'U'])
return pd.concat([df['Pclass'], df_sex, df['SibSp'], df['Parch'], df_fare, df_age, df_emb],axis=1)
# 学習に使用するデータを整形する
df_X = transform_data(df_train)
df_y = df_train['Survived']
# Feature Scaling
df_X = df_X.dropna()
sc = StandardScaler()
df_X = sc.fit_transform(df_X)
# 一応テストデータも整形しておく
df_X_test = transform_data(df_test)
df_X_test = sc.transform(df_X_test)
SVMを試してみる
まずは、SVM(=Support Vector Machine)を試してみます。
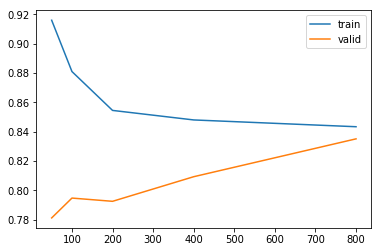
learning_curveメソッドを用いて、学習の収束度合いも見てみます。
train_sizes, train_scores, valid_scores = learning_curve(SVC(kernel='rbf', C=4, gamma=0.075), df_X, df_y, train_sizes=[50, 100, 200, 400, 800], cv=10)
plt.plot([50, 100, 200, 400, 800], train_scores.mean(axis=1), label='train')
plt.plot([50, 100, 200, 400, 800], valid_scores.mean(axis=1), label='valid')
plt.legend()
plt.show()
print(valid_scores.mean(axis=1))
[0.78118006 0.79471399 0.79250482 0.80928442 0.83510328]
Neural Networkを試してみる
次に Neural Network を試してみます。
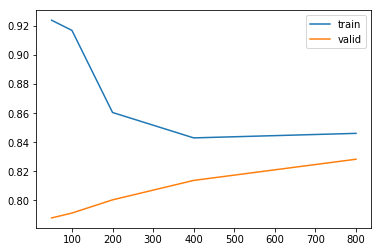
train_sizes, train_scores, valid_scores = learning_curve(MLPClassifier(hidden_layer_sizes=(128), alpha=1 , random_state=1, solver="adam" ,max_iter=10000), df_X, df_y, train_sizes=[50, 100, 200, 400, 800], cv=10)
plt.plot([50, 100, 200, 400, 800], train_scores.mean(axis=1), label='train')
plt.plot([50, 100, 200, 400, 800], valid_scores.mean(axis=1), label='valid')
plt.legend()
plt.show()
print(valid_scores.mean(axis=1))
[0.78791 0.7912683 0.80034474 0.81372858 0.82831092]
決定木を試してみる
決定木も試してみます。
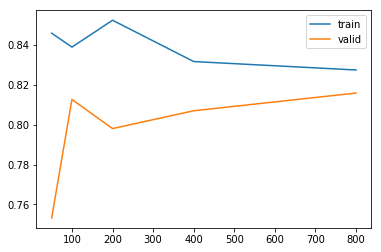
train_sizes, train_scores, valid_scores = learning_curve(tree.DecisionTreeClassifier(max_depth=3), df_X, df_y, train_sizes=[50, 100, 200, 400, 800], cv=10)
plt.plot([50, 100, 200, 400, 800], train_scores.mean(axis=1), label='train')
plt.plot([50, 100, 200, 400, 800], valid_scores.mean(axis=1), label='valid')
plt.legend()
plt.show()
print(valid_scores.mean(axis=1))
[0.75316536 0.81268017 0.79806095 0.80701169 0.81591278]
提出データの作成
もっとも予測精度が高かったSVMを用いて学習し、テストデータの生死ラベルを予測します。
予測結果は、pandas.to_csvメソッドを用いてCSVファイルに出力します。
# もっとも予測精度がよかったSVMを用いて学習する
model = SVC(kernel='rbf', C=4, gamma=0.075)
# 学習データを全部使用して学習する
model.fit(np.array(df_X), np.array(df_y))
# 生死の予測
result = np.array(model.predict(df_X_test))
df_result = DataFrame(result, columns=['Survived'])
# 提出データには乗客IDが必要なので、連結する
df_result = pd.concat([df_test['PassengerId'], df_result], axis = 1)
# 生死の予測値は [0,1] の範囲の実数なので、2値化する
df_result['Survived'] = np.array(round(df_result['Survived']), dtype='int')
df_result.to_csv('reult_svc_titanic.csv', index=False)
結果
作成したデータをKaggleにアップロードすると、すぐに結果(予測精度)が算出されます。
今回の結果は、0.78468でした。(大体 3,500/10,600 くらいの順位です)
CrossValidationの結果からすると、8割は超えていると思ったのですが・・・
次回は8割越えを目標に、いろいろ試してみようと思います。