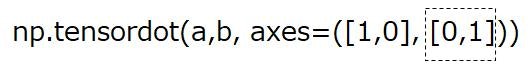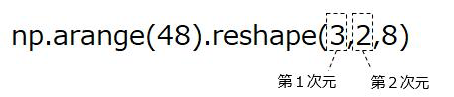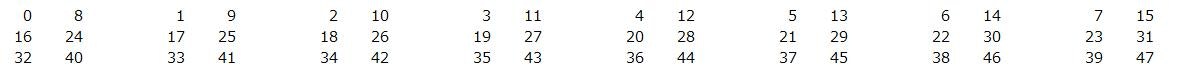numpyのtensordot(テンソル積)が壊滅的に分からなかったのですが、いろいろ調べてそれなりに理解できた感があるので、メモしておこうと思います。
今回の題材
>>> import numpy as np
>>> a = np.arange(12).reshape(2,3,2)
>>> b = np.arange(48).reshape(3,2,8)
>>> c = np.tensordot(a,b, axes=([1,0], [0,1]))
>>> a
array([[[ 0, 1],
[ 2, 3],
[ 4, 5]],
[[ 6, 7],
[ 8, 9],
[10, 11]]])
>>> b
array([[[ 0, 1, 2, 3, 4, 5, 6, 7],
[ 8, 9, 10, 11, 12, 13, 14, 15]],
[[16, 17, 18, 19, 20, 21, 22, 23],
[24, 25, 26, 27, 28, 29, 30, 31]],
[[32, 33, 34, 35, 36, 37, 38, 39],
[40, 41, 42, 43, 44, 45, 46, 47]]])
>>> c
array([[ 800, 830, 860, 890, 920, 950, 980, 1010],
[ 920, 956, 992, 1028, 1064, 1100, 1136, 1172]])
np.tensordotでやっていること1: 行列aから中間行列を生成する
行列aの第2次元、第1次元の順番で要素を拾い、演算用の中間行列をつくる、というイメージです。
その中間行列の形状は、第2次元数 × 第1次元数 となります。
今回の場合は、3(第2次元数)×2(第1次元数) の形状の、中間行列がつくられるイメージです。
どんな場合でも、左上の要素を最初に拾います。
この次にどこの要素を拾うか、となるわけですが
第2次元、第1次元の順番に拾うわけですので、
まずは第2次元の順番に拾っていきます。
第2次元の順番に拾うとこうなります。
さらに、この次にどこの要素を拾うか、となるわけですが
第2次元の順番に拾いきりましたので、
次は第1次元の順番に沿って、「下」の島にジャンプします。
さきほどと同じように、「下」の島でも第2次元の順番で要素を拾います。
これで、3×2の行列ができました。
「右」側に対しても、同様のことをやっていきます。
これで、3×2の行列の二つ目ができました。
結果、以下のような構造ができます。
np.tensordotでやっていること2: 行列bから中間行列を生成する
行列bの第1次元、第2次元の順番で要素を拾い、演算用の中間行列をつくる、というイメージです。
その中間行列の形状は、第1次元数 × 第2次元数 となります。
今回の場合は、3(第1次元数)×2(第2次元数) の形状の、中間行列がつくられるイメージです。
どんな場合でも、左上の要素を最初に拾います。
この次にどこの要素を拾うか、となるわけですが
第1次元、第2次元の順番に拾うわけですので、
次は、「下」の島にジャンプしなければなりません。
第1次元の順番に拾うとこうなります。
さらに、この次にどこの要素を拾うか、となるわけですが
第1次元の順番に拾いきりましたので、
次は第2次元の順番に沿って、「一番上」の島に戻ります。
④から再出発しつつも、さきほどと同じように第1次元の順番で要素を拾います。
これで、3×2の行列ができました。
残りに対しても、同様のことをやっていきます。
3×2の行列が8つできるはずです。
結果、以下のような構造ができます。
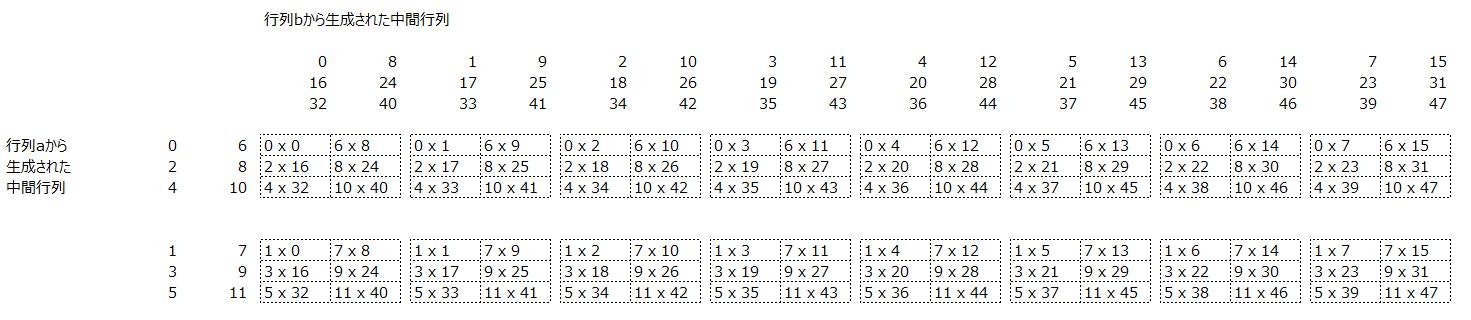
np.tensordotでやっていること3: 行列a、行列b から得られた2つの中間行列について「積」をとる
2次元 × 8次元の行列にコンパクト化されました。
概念的には何をやっているのか
これらの次元について計算することで、これらの次元の情報を保ちつつ、これらの次元を削減し、
残ったこれらの次元(つまり2次元 × 8次元)の形状に、コンパクト化しているわけです。
こういった意味で、このような操作を縮約と呼ぶようですね。
「縮小 + 要約」 ということだと解釈してます。
テンソル積というのはこういうことみたいですね。