はじめに
Q-Qプロットについて解説している記事はいろいろありますが、もっと素人的な使い方を紹介します。
Q-Qプロットの立ち位置
Q-Qプロットとは2つの分布がどれだけ似ているかを視覚的に確認するためのツールです。
しかし「2つの分布AとBがどれだけ似ているか」を頻繁に確認したい業務はあまり多くないと思います。
製造業などでは特に、「分布がどれだけ違うか、変化したか」を確認したいはずです。
似ていない分布AとBをそれぞれ横軸、縦軸にプロットしても直感的ではありません。
ただし分布Aを標準正規分布に固定して、1次元のデータとして分布BをプロットしたQ-Qプロットには、メリットがあります。
Q-Qプロットの実例
47nFのコンデンサを98個買ってきて、念のため容量を測定してみました。
大変なので33個、36個、29個ランダムにサンプルを分けて3人で測定しました。
結果をQ-Qプロットで表すと以下のようになります。
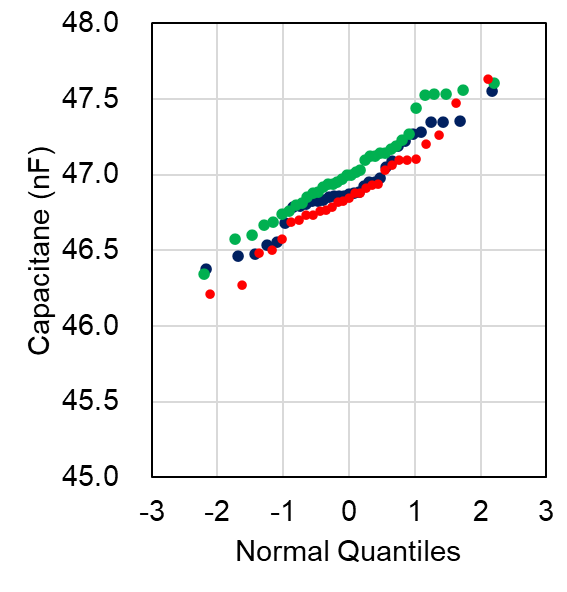
測定する人による差(4MのMan)はまぁ、ちょっとあるけれど許容範囲か?といった感じです。
赤の人が小さめに値を記録しているようなので、検定をすれば有意な差が出るでしょう。
次回も同様の分布になったら、作業を監督して赤(または緑)の人のクセを直した方がよさそうです。
もちろん、製造ラインの立ち上げ中とかで、このデータが装置間のばらつき等だったら、そんなのんきなことを言っていないで即調整指示が飛ぶでしょう。
ヒストグラムと比較したときのQ-Qプロットのメリット
1次元のデータを可視化する定番はヒストグラムですが、区間の設定にコツが要ります。
粗すぎても細かすぎても、キレイな釣り鐘型にはなりません。
また、今回は全体的に0.2nFほど分布がズレていましたが、例えばヒストグラムの区間を0.5nFにしてしまうと、この差が見えにくくなります。
一方、Q-QプロットをExcelで描く場合、データの隣に1列追加するだけの散布図なので簡単です。
また実測値すべてを独立した点で表現するので、データを直読できます。
最大、最小、中央値を一瞬で読み取れます。
分散は点列の傾きで傾向を見ることができます(値自体は素直に元データから計算)。
データの数はバラバラで、次回はまた変わるでしょう。しかし問題ありません。
ヒストグラムと比較したときのQ-Qプロットのメリットをまとめると、以下のようになると思います。
- 手持ちのデータが正規分布かどうかをざっくり確認できる
- 3つ以上の分布でも、横軸を共通にして一度に比較できる
- 細かいパラメータ調整が不要で、描画が楽
- データ数の異なる分布を換算等せずに比較できる
- 正規分布は有名なので(
統計を知らない人ほど)納得してもらいやすい
人によっては、正規分布かどうかなんてどうでもいいかもしれません。
それでもQ-Qプロットは役に立つと思います。
グラフの横軸の意味
データ数$n$だけ与えれば横軸の値を自動的に定めることができます。
これこそが、Q-Qプロットが複数の分布を比較しやすい理由でした。
グラフ自体は統計ソフトにデータを流し込むだけで一瞬で描出されますが、ちょっと遠回りをして、ここでは横軸の意味を考えます。
十分大きい$n$個の昇順に並んだデータ$\{a_n\}$が標準正規分布に従うと仮定します。
a_1,\,a_2,\,\cdots,\,a_n
この分布のようすをグラフにすると標準正規分布の定義から下記のようになります。
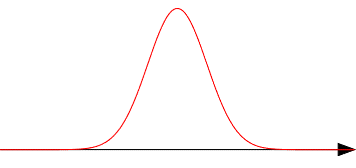
$a_k$が中央値付近の値であれば、$a_k$の隣のデータ($a_{k-1}$や$a_{k+1}$)は$a_k$と近い値になると考えられ、この分布内のデータとしては「多い部類」になりますが、実際のそれぞれの出現回数は1回か、せいぜい2回です。
つまり、ある実験データ$x$があったとして、それがピッタリ$a_k$と等しい確率は、それがどんな$a_k$であってもほぼゼロです。
下図において赤色の長方形の面積がその確率になるわけですが、幅がゼロなので。
P_k(x=a_k)\simeq0
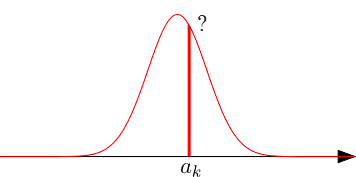
事ここに至りて、累積分布の方が扱いやすいということがわかります。
\mathit{\Phi}(x)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^x \mathrm{e}^{-t^2/2}\mathrm{d}t
ある実験データ$x$が$a_k$以下である確率ならば表現できます。
P_k(x\leq a_k)=\mathit{\Phi}(a_k)
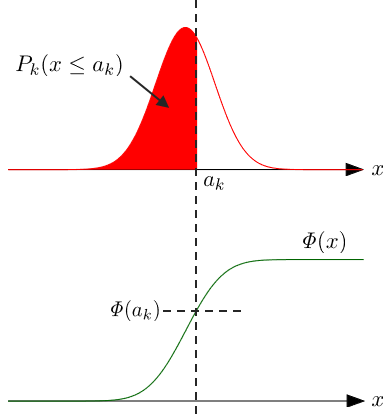
ところで、$n$が十分大きければ、ある実験データ$x$が$a_k$以下となる確率は$k$と$n$のみで記述できます。
P_k(x\leq a_k)=\frac{k-0.5}{n}
この表式については様々なサイトで議論されています。
$\frac{k}{n+1}$を採用するところもあります。
ただ一番直観的な$\frac{k}{n}$はダメです。
これだと$k=n$のとき確率が$1$になってしまいます。0%と100%はありえません。
以上より、$n$が十分大きく、$\{a_n\}$が標準正規分布に従うならば
a_k=\mathit{\Phi}^{-1}\left(\frac{k-0.5}{n}\right)
と表されます。
「標準正規分布の累積分布の逆関数」$\mathit{\Phi}^{-1}(x)$をプロビット関数といい、今回の例ではデータ数$n$と順位$k$を与えれば近似値が得られます。
上式の左辺を縦軸、右辺を横軸にとれば原点を通る傾き1の直線になります。
実際の正規分布に従うデータにおける平均や分散はそれぞれ標準正規分布とは異なるため、グラフのy切片と傾きは変わりますが、直線性は維持されます。
これがQ-Qプロットの直線性になります。
注意事項
- 今回の事例はフィクションです
- データがたとえ3個しかなくてもQ-Qプロットなら描画できてしまいます。グラフを解釈する前にn数を確認しましょう
まとめ
Q-Qプロットは統計の素人でも使い道がある例を紹介しました。