想定読者
-
零知識証明 / zk-SNARKs について知りたい人
- 特に理論的側面を知りたい人
- 「zk-SNARKs って何だ?」という人
概要
zk-SNARKs に関する ELECTRIC COIN CO. の解説記事 に簡単に補足をしながら紹介するシリーズ Part 5 です。
Part 5 のテーマは From Computations to Polynomials(計算から多項式へ) です。
Part 41までで準備を終え、非対話零知識証明の核心に迫っていきます。とはいうものの、このパートでは、まだ非対話の話ではなく、対話の話がメインになります。さらにその中でも、 証明者(アリス。認めてもらう側)がどのように情報をコンパクトにし情報を送るか がメイントピックになっています。この点を意識しながら読んでいただけるとわかりやすいかと思います。
読み方
Part 1 の解説記事の 読み方 と同様です。
込み入った議論や数学的に細かい部分は注釈(foot note)にまとめました。そのため、注釈が多くなっていますが、注釈を読まなくても大丈夫ですので、読み飛ばしていただいて構いません。
From Computations to Polynomials
対応する記事
Explaining SNARKs Part V: From Computations to Polynomials
一言でいうと
アリス(証明者)はボブ(検証者)に送る情報を算術回路(arithmetic circuit)を経由して、QAP(quadratic arithmetic program)に関する多項式に変換することができる
※ これまでのパートで、アリスがボブに対して多項式をうまく伝える方法について議論していましたが、ここで多項式の伏線が回収されるわけです
Part 4の振り返り
前回のパートまでで、以下の点が説明されていました。
- アリスがボブに多項式を知っていることを(ゼロ知識風に)伝えることができること
- $\alpha$-ペアを利用することで、ボブはアリスが送る情報をある程度制限できること
このパートでは上記の知識はほとんど使いません。どちらかというと、「なんで多項式伝えようとしているんだっけ?」という問いへの答えがあります。
はじめに
このパートでは、情報をQAPに変換していきます。ただ、それぞれの理論の一般理論やその証明はここでは触れず具体例を通して何をやっているのかを掴んで頂くことになるので注意してください。
具体的に以下の状況を考え、算術回路を経由してどのようにQAPへ変換されるかを確認していきます。
アリス(証明者)は $ (c_1 \cdot c_2) \cdot (c_1 + c_3) = 7 $ を満たす $ c_1, c_2, c_3 \in \mathbb{F} _ p $ を知っていることをボブ(検証者)に伝えたい
算術回路(arithmetic circuit)への書き換え
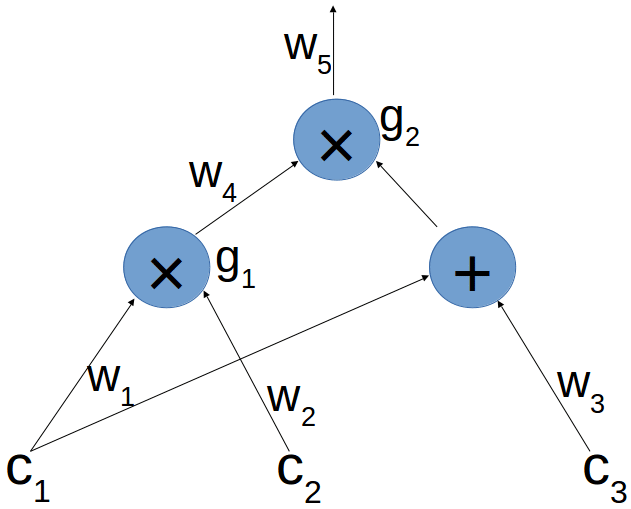
$ (c_1 \cdot c_2) \cdot (c_1 + c_3) $ を算術回路に書き換えます。先に図を見るほうが雰囲気はつかめるかもしれません。
特徴としては
- グラフのノード(節)に当たる部分には演算子である $ + , \times $ が入っている
- ノードはエッジ(辺)でつながっており、それぞれの演算の入力と出力を表している
- 最初の入力部に $ c_1, c_2, c_3 $ が入っている
例えば、 $g_1$ のノードには、 $w_1, w_2$ が入力として入り、 出力として $w_4$ が出ており、これは、 $ (c_1 \cdot c_2) \cdot (c_1 + c_3) $ の $ (c_1 \cdot c_2) $ の部分を表していることがわかります。
注意するべきことは、演算子は平等ではないということです。ここがとっつきにくいのですが、こういうものだと思っていただく方が話は早いです。 掛け算の方だけそれぞれの部分的な計算結果に $c_n$ を代入することにします。つまり、
- $ c_4 = c_1 \cdot c_2 $
- $ c_5 = c_4 \cdot (c_1 + c_3) $
というように置くことにします。なぜ足し算の方はそのままで掛け算だけこうするのか気になりますが3、ここでは深入りしません。これは、図では $+$ の方には $g$ が定義されておらず、 $\times$ の出力にみ $w$ の文字が当てられていることと対応しています。
天下り的な部分が多いですが、これらを認めることで、以下のように情報が変換されました。
- 変換前: アリス(証明者)は $ (c_1 \cdot c_2) \cdot (c_1 + c_3) = 7 $ を満たす $ c_1, c_2, c_3 \in \mathbb{F} _ p $ を知っている
- 変換後: アリス(証明者)は上の算術回路を満たす$c_5 = 7$ となるような $ c_1, \ldots , c_5 \in \mathbb{F} _ p $ を知っている
QAP(quadratic arithmetic program) への簡約
設定・記号の導入
以下の記号を導入します。
- $L_1, \ldots, L_5$ ... 左入力ワイヤ多項式(左から入力される $w$ に関する多項式)
- 例: $w_1$ が左から入力されるときの多項式を $L_1$ と置く
- $R_1, \ldots, R_5$ ... 右入力ワイヤ多項式(右から入力される $w$ に関する多項式)
- 例: $w_2$ が右から入力されるときの多項式を $R_2$ と置く
- $O_1, \ldots, O_5$ ... 出力ワイヤ多項式(出力される $w$ に関する多項式)
- 例: $w_4$ が出力されるときの多項式を $O_4$ と置く
また、議論の本質にフォーカスするために $g_1$ を $1 \in \mathbb{F} _ p $ とみなし、$g_2$ を $2 \in \mathbb{F} _ p$ とみなすことにします。そして、この $g_1, g_2$ をターゲットポイントと呼びます。
ターゲットポイントで0になる多項式
これまた天下り的ですが、上で定義した $L_1, \ldots, L_5, R_1, \ldots, R_5, O_1, \ldots, O_5$ の多項式をターゲットポイントにおいて$0$ になるようにします。ただし、それだとすべて多項式としての $0$ とすればよいだけになってしまうので、次の例外を課します。
- ターゲットポイントと対応する掛け算のノードに関する多項式に関しては、そのターゲットポイント上で 0 にならないようにする
具体的に構成することで、この意味もわかりやすくなると思います。
$g_1$ に関する多項式について考えます。$w_1$ が左からの入力、 $w_2$ が右からの入力、$w_4$ が出力となっていますので、それぞれの多項式を以下のように定義します。
$$
L_1 = R_2 = O_4 = 2 - X
$$
これは、
- $X$ に $g_1$ に対応する $1$ を代入すると $1$
- $X$ に $g_2$ に対応する $2$ を代入すると $0$
となることがわかります。 $g_1$ に関する多項式が $g_1$ においては $0$ にならないようになっています。
$g_2$ に関しても同様に考えると次のように多項式を定義できます。
$$
L_4 = R_1 = R_3 = O_5 = X - 1
$$
$g_2$ に関する多項式が $g_2$ においては $0$ にならないようになっています。また、 $w_1$ と $w_3$ は足し算のノードを通じて $g_2$ に入っているので、両方とも右からの入力と捉えている点にも注意してください。
そして、その他の"余った"多項式は例外パターンでもないので、多項式として $0$ とします。わかりやすさのために、書き下すと以下のようになります。
\begin{align}
L_1 &= 2 - X, \ L_2 = 0, \ L_3 = 0, \ L_4 = X - 1, \ L_5 = 0 \\\\
R_1 &= X - 1, \ R_2 = 2 - X, \ R_3 = X - 1, \ R_4 = 0, \ R_5 = 0 \\\\
O_1 &= 0, \ O_2 = 0, \ O_3 = 0, \ O_4 = 2 - X, \ O_5 = X - 1
\end{align}
特定の条件でのみ、すべてのターゲットポイント上で 0 になる多項式 P
これまでの結果を利用すると、都合の良い性質を持つ多項式 $P$ を定義することができることが知られています。都合の良い性質というのは、以下の2つが同値(必要十分条件)である性質です。
- $ c_1, \ldots , c_5 $ が算術回路への正しい代入である
- ($ c_1, \ldots , c_5 $ を用いて定義される) $P$ はすべてのターゲットポイント上で $0$ になる
最初の概要で書いたように、これによって、最初の情報が多項式 $P$ に変換されていることに気づかれたと思います。最後に$P$の構成方法に触れた後、具体的に $P$ がその性質を満たしていることを確認します。
とある値$ c_1, \ldots , c_5 $ 4を使って 、以下のように先程の多項式達から次の新たな多項式を定義します。
L = \sum _{i=1} ^ 5 c _ i \cdot L _ i \\\\
R = \sum _{i=1} ^ 5 c _ i \cdot R _ i \\\\
O = \sum _{i=1} ^ 5 c _ i \cdot O _ i \\\\
P = L \cdot R - O
これで $P$ を構成することができました。では、先程紹介した次の性質を満たすかを確認します。
以下の2つが同値(必要十分条件)である性質です。
- $ c_1, \ldots , c_5 $ が算術回路への正しい代入である
- ($ c_1, \ldots , c_5 $ を用いて定義される) $P$ はすべてのターゲットポイント上で $0$ になる
$P$ がすべてのターゲットポイント上で $0$ になるための $ c_1, \ldots , c_5 $ の条件を導き、それがもとの $ (c_1 \cdot c_2) \cdot (c_1 + c_3) = c_5 $ と同値であることを確認できれば良いですね。
ターゲットポイント $g_1 = 1$ における $L, R, O$ を考えます。
\begin{align}
L &= c_1 \cdot (2 - X) + c_4 \cdot (X - 1) \\\\
R &= c_1 \cdot (X - 1) + c_2 \cdot (2 - X) + c_3 \cdot (X - 1) \\\\
O &= c_4 \cdot (2 - X) + c_5 \cdot (X - 1)
\end{align}
において、 $X = 1$ で評価すると、$L, R, O$が求まり、$P$ も計算できます。
\begin{align}
L &= c_1 \\
R &= c_2 \\
O &= c_4 \\
P &= L \cdot R - O = c_1 \cdot c_2 - c_4
\end{align}
ターゲットポイント $g_2 = 2$ における $P$ も同様に $X = 2$で評価することで
P = c_4 \cdot (c_1 + c_3) - c_5
であることがわかります。これらが同時に $0$ になるとき、
\begin{align}
&c_1 \cdot c_2 - c_4 = c_4 \cdot (c_1 + c_3) - c_5 = 0 \\
\Leftrightarrow \ & (c_1 \cdot c_2) \cdot (c_1 + c_3) = c_5
\end{align}
となるので$P$の性質が確認できました。
ターゲット多項式 T
ターゲット全てで $0$ になるような多項式 $T$ を考えると、$P$ の性質から、多項式の"割り算"の性質から、次の言い換えも可能です、5
以下の2つは同値である。
- $ c_1, \ldots , c_5 $ が算術回路への正しい代入である
- ($ c_1, \ldots , c_5 $ を用いて定義される) $P$ はターゲット多項式で割り切れる
具体的にいうと、これまでの例だと多項式 $T$ は次のようになります。
T = (X - 1) \cdot (X - 2)
QAP(quadratic arithmetic program)へ
これですべての準備が整ったので、最後に QAP の一般的な形で紹介し、情報がどのように変換されたかを確認します。
サイズ $m$, 次数 $d$ の QAP $Q$ は以下で構成される。
- 多項式 $L_1, \ldots, L_m, R_1, \ldots, R_m, O_1, \ldots, O_m$
- 次数 $d$ のターゲット多項式 $T$
さらに次の性質を持つ
- $T$ が $P$ を割り切るなら、代入 $ c_1, \ldots , c_m $ は $Q$ を満たす
- ただし、$ L = \sum _{i=1} ^ m c _ i \cdot L _ i, \ R = \sum _{i=1} ^ m c _ i \cdot R _ i, \ O = \sum _{i=1} ^ m c _ i \cdot O _ i $ であり、 $P = L \cdot R - O$ とする
これを具体例に当てはめることで
- アリス(証明者)は $ (c_1 \cdot c_2) \cdot (c_1 + c_3) = 7 $ を満たす $ c_1, c_2, c_3 \in \mathbb{F} _ p $ を知っている
が算術回路のバージョンを経由して、最終的に
- アリス(証明者)は $c_1, \ldots , c_5$ を用いて QAP を構成し、 $T$ が $P$ を割り切るようにすることができる
という形に変換されることがわかります。
これでめでたく、アリスの知識(情報)が QAP に変換され多項式$P$ に集約されることが確認できました ![]()
まとめ
- 送信する情報を算術回路(arithmetic circuit)で表現することができる
- 算術回路(arithmetic circuit)はQAP(quadratic arithmetic program)に等価に変換できる
- 上記により、送信する情報を多項式で表現することができる
次回は Part 6(How to make Blind Evaluation of Polynomials Verifiable) です。このパートが、アリス(証明者)側の工夫であるとすると、次のパートはボブ(検証者)側の工夫の話です。如何にボブがうまく(簡単に)検証することができるかという話が展開されていきます。
-
これは筆者の勉強不足で詳しくわかっていませんが、 $\times$ と $+$ のどちらかを特別視することで表現の一意性を担保しているためと思われます。つまり、 $\times$ と $+$ の出力両方に $c_n$ などを割り当てることを認めてしまうと、同等の算術回路を複数構成できてしまうので、それを避けているのではないかというわけです。ある多項式が一つあってそれを算術回路に変換する際に、いろんな変換先があると対応関係が複雑になり、理論がきれいに書きにくいからなのかなと考えています。(一般的に、変換の方法や変換先が一意に定まるような、一対一の等価な関係性の方が理論を書くときに書きやすいので、くらいの経験から予想しています) ↩
-
算術回路への正しい代入である必要はありません。これらの値が算術回路への正しい値の場合にのみ、$P$ はすべてのターゲットポイントで $0$ になりますが、$P$ 自体の定義としては、 $ c_1, \ldots , c_5 $ に制約は不要です。 ↩
-
高校数学でやった多項式の割り算、というやつです。 ↩