この記事は第3回目です。このシリーズの概要と前回までの内容は以下の記事になります。よければそちらもお読み下さい。
内容は Python 100% です。
再帰
プログラムにおける 再帰 recursion とは、ある関数がその定義の中で自己参照されているものを言います。マトリョーシカのようなイメージです。この辺の説明は例の如く、他の良記事にお任せするとしましょう。こちらの説明は非常にわかりやすいと思います。
再帰関数を使うには、
- 終了条件・基底(上の記事で言うベースケース)を明記
- 再帰呼び出しを行うことで、終了条件に近づくようにする(数が小さくなる、範囲が狭くなる、etc)
この2つの条件を満たすことが不可欠です。そうでないと無限ループに陥りますね。一番わかりやすい階乗 $n!$ を Python で実装すると以下のようになります。
def factorial(n):
if n == 1: # 終了条件
return 1
else:
return n * factorial(n-1) # n! = n * (n-1)!
$n!$ は $n \times (n-1)!$ と分解でき、$(n-1)!$ は $(n-1) \times (n-2)!$ と分解できるので、同様に小さく分解していけば最終的に終了条件の 1 にたどり着くという理屈です。
もう一つ、再帰の代名詞とも言えるフィボナッチ数列も考えましょう。
これは 1, 1, 2, 3, 5, 8, 13, ... と前の2つを足していくので、最初の2つの数を終了条件として定義し、それ以降は再帰呼び出しで求められます。
def fibo(n):
if n == 1:
return 1
elif n == 2:
return 1
else:
return fibo(n-1) + fibo(n-2)
実際にこのコードで実装すると一瞬で破綻する という話はこの後するとして、この形って高校数学のあの分野そのものだと思いませんか?そうです、漸化式 / 数学的帰納法です。
漸化式
漸化式 recurrence relation が何かについては理解しているものとして話を進めます。上記のフィボナッチ数列の場合、以下のような漸化式 (帰納的定義) として書けます。
\displaylines{
F_1 = 1 \\
F_2 = 1 \\
F_n = F_{n-1} + F_{n-2}
}
漸化式は、数列における隣接する項の 関係 を示したものに過ぎません。数列 {$a_i$} の n 番目の具体的な値 $a_n$ が知りたい場合には、
- 漸化式を解き、一般項 $a_n$ を $n$ の関数として求める
- 漸化式を使い、1 から n まで帰納的に計算する
のどちらかを選択する必要があります。(1) の場合は漸化式を解いて一般項を求める必要があります。例えば、
\displaylines{
a_1 = 2 \\
a_n = 3a_{n-1} -2\\
}
のようなシンプルな線形漸化式であれば、一般項を $a_n = 3^{n-1} + 1$ のように求めることができますので、ダイレクトに $a_n$ の具体的な値を計算することが可能になります。
ただ、漸化式は解けない場合も多く、例えば
\displaylines{
a_1 = 1\\
a_n = (a_{n-1}+1)^2 + 1\\
}
のような場合だと一般項が求められないので、仕方なく $a_1=1, a_2=5, a_3=37$ と帰納的に計算していかなければなりません。
以上は数学での例ですが、この「解けるか解けないか」という点はプログラムの実装においても重要で、再帰を使ったプログラムを書く際には、「本当にこれは再帰を使わなければならないのか?」と一旦考えてみることが必要になります。直接計算が可能ならば帰納的に計算するのは無駄だとも考えられるからです。直接求めるのが困難だから「仕方なく」帰納的に計算する、とも言えます。
ちなみに、フィボナッチ数列の漸化式は解けます。一般項は以下のようになります。
F_n = \frac{1}{\sqrt{5}} \left\{ \left( \frac{1+\sqrt{5}}{2} \right)^n - \left( \frac{1-\sqrt{5}}{2} \right)^n \right\}
って、こんなの知らなきゃ無理だろというレベルですし(3項間漸化式の公式で解けるので、一応高校範囲ではありますが...)、いちいちこんなものを解いてから実装なんて割に合いません。1から順に計算していった方が遥かにマシです。コンピュータの利点は人間よりも圧倒的に速く計算できることなのですから、人間がわざわざ代数的・解析的に求めるよりも、力技で数え上げた方が楽なこともしばしばあります。ですので、「仕方なく」帰納的に計算するとは言ったものの、そちらの方が効率的なら実際に計算すればいいのです。
帰納的に計算する ≠ 再帰
「漸化式が解けない場合は帰納的に計算していくしかない」と言いましたが、それは必ずしも再帰(関数の定義内で自身の関数を呼び出す)の利用を意味するわけではありません。再帰を使わなくても、帰納的に順に計算することはできるからです。
フィボナッチ数列での一番単純な例が以下です。計算結果の数値を 1 から順に配列に格納していくということです。実装すると以下のようになります。
def fibo(n):
array = [0, 1, 1]
if n <= 2:
return array[n]
else:
for i in range(3, n+1):
array.append(array[-1] + array[-2])
return array[n]
配列 array を用意し、その中に順々に計算結果を格納していき、$F_n$ を取り出すという作業をやっています。この場合、関数 fibo 内で自分自身を呼び出す必要はありません。
「最後の2つだけ分かればいいんだから、それ以前の計算結果は捨てちゃっても構わないんじゃないか?」と思った方、その通りです。n が大きい場合、その方が空間計算量(メモリ)の節約にもなります。少し改良してみましょう。
def fibo(n):
Fn_1 = 1 # Fn-1 (初期状態では F1)
Fn = 1 # Fn (初期状態では F2)
if n == 1:
return Fn_1
elif n == 2:
return Fn
else:
for i in range(3, n+1):
Fn, Fn_1 = Fn + Fn_1, Fn # Fn と Fn-1 の更新
return Fn
これだと、常に最後の2つの数字だけを保持しながら次の値を順々に計算していくことになります。いずれにせよ再帰は使っていません。
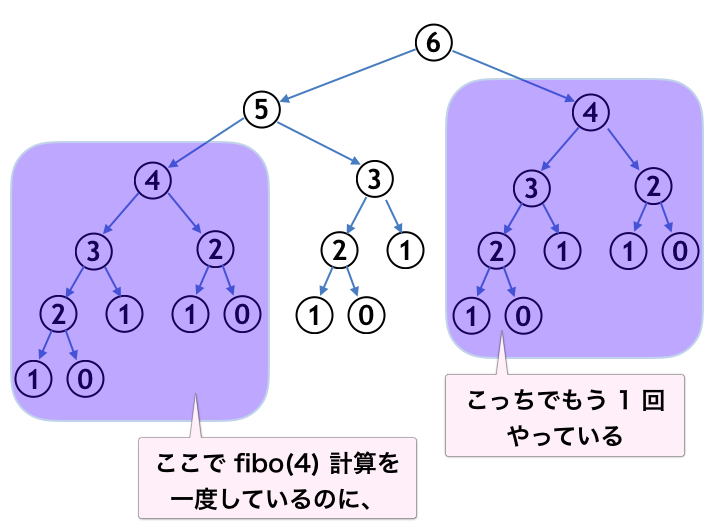
数値格納だろうが再帰だろうが、結局終了条件から帰納的に計算しているという点では同じなのでは?と思われるかもしれませんが、計算量としては大きな違いがあります。上述のリンクを再掲し、画像をお借りいたします。
ここに説明がある通り、再帰で呼び出した場合に以前に計算した結果があっても、それを再利用せずに再び計算してしまうという無駄が生じています。以下の図を見るとわかりやすいですが、分岐が倍々していくので指数関数となり、時間計算量は $O(1.618^n)$ という非常に効率の悪いものになります。
これはフィボナッチ数列が「3項間漸化式」であるというのが理由で、単純な隣接2項間の漸化式を再帰で実装したならば、分岐がないので $O(n)$ となります。数値格納は 1 から n まで順に計算しているだけなので、同様に $O(n)$ です。
実際にどのくらいの差が出るのか、notebook 上で実験してみましょう。再帰関数でフィボナッチ数列の $F_{40}$ を求めると以下のようになります
%%time
def fibo(n):
if n == 1:
return 1
elif n == 2:
return 1
else:
return fibo(n-1) + fibo(n-2)
fibo(40)
CPU times: user 12.9 s
102334155
13秒もかかっていますね。では、数値格納の方でやってみます。
%%time
def fibo(n):
Fn_1 = 1 # Fn-1 (初期状態では F1)
Fn = 1 # Fn (初期状態では F2)
if n == 1:
return Fn_1
elif n == 2:
return Fn
else:
for i in range(3, n+1):
Fn, Fn_1 = Fn + Fn_1, Fn # Fn と Fn-1 の更新
return Fn
fibo(40)
CPU times: user 14 µs
102334155
同じ計算が100万分の1の時間で終了しました。当然ながら、再帰の方では $F_{100}$ などを求めることは不可能です。数値格納ならば、10万でも1秒以内に終わります、答えは 20899 桁というとんでもない数になりますが。
ちなみにこの方法は、動的計画法 Dynamic Programming (DP) のボトムアップ方式と言われるものの一種になります。DP に関しては、今後の記事でもちょくちょく出てくることになるでしょう。
メモ化再帰
再帰における再計算を回避する方法として、メモ化 memorization という方法もあります。これは「既に計算した結果はどこかに保存しておき、それを再利用する」というものです。上述のボトムアップ方式と同じように見えますが、別に 1 から順番にやっていかなければならないわけではありません。計算結果が出たものから順々にメモを行なっていけばいいということです。再帰は n → n-1 → n-2 と上から順に辿っていくので、こちらはトップダウンの方法になります。↑ の wiki によると、メモ化再帰も動的計画法の一種となっていますが、ボトムアップのものだけを動的計画法と呼ぶことも多いようです。
Python での実装例は以下です。
memo = {1:1, 2:1} # メモ用の辞書を作成、F1 と F2 を用意
def fibo(n):
if n in memo:
return memo[n] # メモに数値がある場合、その値を返す
else:
fn = fibo(n-1) + fibo(n-2) # 再帰呼び出し
memo[n] = fn # メモに無い答えなので、新たに追加しておく
return fn
メモ用の辞書の代わりに、長さ n の配列を使っても同じです。これを使って時間を計測してみましょう。
%%time
memo = {1:1, 2:1}
def fibo(n):
if n in memo:
return memo[n]
else:
fn = fibo(n-1) + fibo(n-2)
memo[n] = fn
return fn
fibo(1000)
CPU times: user 766 µs
43466557686937456435688527675040625802564660517371780402481729089536555417949051890403879840079255169295922593080322634775209689623239873322471161642996440906533187938298969649928516003704476137795166849228875
$F_{1000}$ でも余裕で計算できます。再計算さえなければ、再帰でも十分高速になることがわかりました。
ちなみに、Python には再帰の際の再計算を回避するためのキャッシュが用意されていて、これを使うと自動的にメモ化を行なってくれます。組み込みモジュールの functools の中にあり、関数の前にデコレータとして配置します。こちらの方が若干動作が速いです。
%%time
from functools import cache
@cache
def fibo(n):
if n == 1:
return 1
elif n == 2:
return 1
else:
return fibo(n-1) + fibo(n-2)
fibo(1000)
CPU times: user 402 µs
43466557686937456435688527675040625802564660517371780402481729089536555417949051890403879840079255169295922593080322634775209689623239873322471161642996440906533187938298969649928516003704476137795166849228875
Paiza で実行する場合、 Python のバージョンは 3.8 のようで(2024/1 現在)、これには functools.cache はありません。代わりに、以下のように lru_cache を使って下さい。
from functools import lru_cache
@lru_cache
def fibo(n):
...
再帰 ≠ 遅い
大学時代に「計算機実験」という授業があり、このフィボナッチ数列の再帰の話を学んで以来、私の中では何となく「再帰は危ない、遅い」という漠然とした偏見がありました。ですが、よくよく考えてみれば上述したようにフィボナッチ数列の再帰が遅いのは3項間漸化式による分岐と再計算のせいであって、再帰そのものが遅いというわけではありません(ただし、再起呼び出しは普通のループに比べスタックに負荷がかかるのは事実)。速いか遅いかは、あくまでそのアルゴリズムの計算量次第です。
再帰のもう一つの有名な例として、ユークリッドの互除法を挙げます。最大公約数を求めるアレです。
例えば、391 と 493 の最大公約数を求めたいなら、
\displaylines{
493 \div 391 = 1 \:\: 余り\:102\\
391 \div 102 = 3 \:\: 余り\:85\\
102 \div 85 = 1 \:\: 余り\:17\\
85 \div 17 = 5\\
}
と、割る数と余りを更新しながら割り切れるまで続け、最後に 17 で割り切れたのでそれが最大公約数になる、というものです。これは Python では以下のように再帰を用いて簡単に実装可能です。
def gcd(n1, n2):
a, b = max(n1,n2), min(n1,n2) # 大きい方を a、小さい方を b にする
if a % b == 0: # 終了条件: 割り切れたらそれが最大公約数
return b
else:
return gcd(b, a % b) # 割る数が次の a に、余りが次の b になる
詳細は wikipedia にも書いてありますが、これの時間計算量は $O(\log n)$ です。二分探索法同様に、割り算を繰り返しているからですね。この場合、while ループを使う代わりに再帰を使って実装した方がコードが若干スッキリするという利点もあります。数値計算法として有名なニュートン法なんかも収束が速く、再帰を使ったからと言って問題になるわけではありません。
要するに、再帰を使う前に、そのアルゴリズムによってどのように範囲が変化していくかの見積もりを行うことが重要だということです。フィボナッチ数列のように、分岐がどんどん増えていくことで再計算が必要になる場合はメモ化の採用が必須になりますが、再帰そのものが遅いというわけではありません。もちろん、While ループ同様に終了条件は明確にしておかなければなりませんし、再帰が深いことによるスタックオーバーフロー や RecursionErrorが起こることがあるので、再帰なしで書けるならばそれに越したことはありません。
いつ再帰を使うべきか?
「再帰じゃないと解けない時」と言ってしまえば終わりなのですが、特に ボトムアップでは解くのが難しい時 です。フィボナッチ数列のように初期値が固定の漸化式ならボトムアップで解けますが、全てがこのように綺麗な数式で表せるわけではありません。スタートの状態が分かりにくく、ゴールからその前の状態へと順に辿っていく場合(木構造やグラフ理論なんかもそうです)では、再帰を使う方が実装が簡単です。
具体的には、以下の練習問題で見てみましょう。
Paiza 問題例
まずフィボナッチ数列はこちらです。「メモ化を使って解いてみましょう」とありますが、メモ化再帰でやると n=10000 などでは RecursionError になるので、素直にボトムアップで数えていくのが良いです。
n = int(input())
def fibo(n):
Fn_1 = 1
Fn = 1
if n == 1:
return Fn_1
elif n == 2:
return Fn
else:
for i in range(3, n+1):
Fn, Fn_1 = Fn + Fn_1, Fn
return Fn
print(fibo(n) % 1000000007)
フィボナッチ数列の応用として、階段の上り方があります。例えば、階段を上るときに、普通に上るか1段飛ばしで上る時、ゴールに達する直前は
- 1段下から普通に上がる
- 2段下から1段飛ばしで上る
の2通りがあることになります。つまり、1段下までの上り方と、2段下までの上り方の合計ということになります。これはフィボナッチ数列そのものです(中学受験でもよく出てきます)。
以下の問題では、一歩で a, b, c 段のどれかで上るとなっています。
これは漸化式で表すと、
$$
F_n = F_{n-a} + F_{n-b} + F_{n-c}
$$
となります。入力も n ≦ 30 と小さめなので、メモ化再帰を使って解きます。注意しなければならないのは、
- 0 段目に行く方法は 1 通り($F_0 = 1$)
- $n-a$ が負になった場合は 0 を返す
(2) があることで、例えば 2 ≦ a, b, c の場合でも $F_1 = 0$ と求められるようになります。
n, a, b, c = map(int, input().split())
memo = {0:1}
def stair(n):
if n in memo:
return memo[n]
elif n < 0:
return 0
else:
way = stair(n-a) + stair(n-b) + stair(n-c)
memo[n] = way
return way
print(stair(n))
from functools import lru_cache
n, a, b, c = map(int, input().split())
@lru_cache
def stair(n):
if n == 0:
return 1
elif n < 0:
return 0
else:
way = stair(n-a) + stair(n-b) + stair(n-c)
return way
print(stair(n))
上記のやり方は再帰を使ったトップダウンの分かりやすい解法ですが、ボトムアップ(動的計画法)でも解けます。漸化式は $F_n = F_{n-a} + F_{n-b} + F_{n-c}$ と3つの項を足すことになりますが、数値格納用の配列や辞書を用意しておき、この3つの項をそれぞれ足していけば良いわけです。解答例は以下です。
n, a, b, c = map(int, input().split())
stairs = {0:1}
for i in range(1, n+1):
stairs[i] = stairs.get(i, 0) + stairs.get(i-a, 0) # i-a がなければ 0 を足す
stairs[i] = stairs.get(i, 0) + stairs.get(i-b, 0)
stairs[i] = stairs.get(i, 0) + stairs.get(i-c, 0)
print(stairs[n])
次にA問題となっているこちらです。
「ある仕事に取り組むためには、その前に指定された仕事を終わらせる必要がある」という制約がある中で、特定の仕事にたどり着く方法は何通りあるか?と言う問題です。これは 有向非巡回グラフ Directed Acyclic Graph (DAG) の典型例でもあります。
これは辞書と再帰を使って解けます。本当はループ路の有無とか、トポロジカルソートだとか色々な話が絡んでくるのですが、それはまた後の機会に話します。とりあえずこの問題は再帰だけを使って簡単に解けるよう上手く作られていると思って下さい。
このような考え方で、全順序を求めることができます。
-
{仕事番号 : [その前に行うべき仕事番号のリスト]}という辞書を作成 - 仕事番号と辞書を入力すると、順序数を返す関数を定義
- その仕事番号をキーとして辞書を参照し、前に行うべき仕事番号のリストを取得
- 前に行うべき仕事がなければ、その仕事だけやればいいので 1 を返す(終了条件)
- 前に行うべき仕事があれば、現在の仕事番号を削除した辞書 を作り、前の仕事番号とその辞書を再帰関数に渡して、その前の仕事までの順序数を取得
- 順序数の和を計算
という流れになります。実はこの問題においては、(3)の「現在の仕事番号を削除」は行わなくてもパスしてしまう問題設定になっているのですが、経路を考える上で「元の位置には戻ってこない」という条件を反映させるためにもあえて削除しています。
n, k = map(int, input().split()) # 仕事数、条件数の取得
orders = {} # 仕事順序用の辞書
for i in range(k):
before, after = map(int, input().split())
orders[after] = orders.get(after, []) + [before] # {仕事番号 : [その前に行うべき仕事番号のリスト]}
def get_route(n, orders): # 関数の定義、目的の仕事番号と辞書を受け取る
if n not in orders: # 前の仕事がなければ、1 を返す
return 1
else:
orders_dropped = orders.copy()
orders_dropped.pop(n) # 現在の仕事番号を除いた辞書を作成
return sum(get_route(x, orders_dropped) for x in orders[n]) # 前の仕事までの順序数の和を返す
print(get_route(n, orders))
このやり方は、前の仕事数が複数あるため分岐の数次第では計算量が大きくなります。2 ≦ N ≦ 10,000 とは書いてあるものの、実際は入力の N の数が小さいためメモ化などを使わなくても問題なくパスしますが、テストケースによってはかなりの時間がかかる可能性がある、ということは念頭においておく必要があります。
最後に、動的計画法に関する問題をもう一問取り上げます。
x 個で a 円、y 個で b 円、z 個で c 円、という3パターンを組み合わせ、n 個以上買う時の最低金額はどうなるか?というものです。これは上述の階段の上り方に似ていますが、単なる漸化式ではなく、最小を考えなければいけません。
例えば x=2, y=3, z=4 の時、10個買うとしたら
- 8個の最小金額 + 2個1セットの金額
- 7個の最小金額 + 3個1セットの金額
- 6個の最小金額 + 4個1セットの金額
を候補とし、その最小を考えれば良いということになります。これも動的計画法を用いて、少ない個数から順々に計算して格納していくことで簡単に解けます。
n, x, a, y, b, z, c, = map(int, input().split())
prices = {0:0} # {合計個数 : 最小金額}
for i in range(1, n+z): # x<y<z なので、個数オーバーしても n+z 未満になる
candidates = []
for num, price in [(x,a), (y,b), (z,c)]: # 個数と価格の組み合わせをループ
if i-num in prices: # 求めたい個数よりちょうど a 個少ない個数の金額がある場合
candidates.append(prices[i-num] + price) # セット金額を足したものを候補とする
if candidates:
prices[i] = min(candidates)
print(min(value for key, value in prices.items() if key >= n)) # n 個以上の中で最小金額を求める
と、今回はここまでになります。次回は ソート について話します。