ゼロ過剰モデルとハードルモデル
ゼロがたくさん含まれるカウントデータを扱うためのモデルとして、**ゼロ過剰モデル(zero-inflated model)とハードルモデル(hurdle model)**というものがあります。
通常のカウントデータを扱うモデルの弱点は、カウントが0のパターンも分布の中に含めてしまうという点です。もちろん、ポアソン分布や負の二項分布からもカウントが0というパターンは生じえます。しかし、カウントが0というデータは、これとは異なったプロセスで生成されている場合が有ります。たとえば値を観測するまでに何らかのハードルがある場合や、一定確率で見逃しが発生するような場合です。このようなデータ生成プロセスでは、ポアソン分布や負の二項分布が想定するよりも多くの0が生ずる可能性があります。
このようなパターンに対処するため、ゼロ過剰モデルとハードルモデルでは、データ生成プロセスを ゼロを生成するプロセス と カウントデータを生成するプロセス に分離して考えます。
ゼロ過剰モデルとハードルモデルはよく似ていますが、根本にある考え方は大きく違い、モデルの選択を間違えると誤った結論に至る危険性もあります。
ハードルモデル
ハードルモデルでは、1段階目のステップとしてベルヌーイ分布による選別を行い、一定の確率で値が0になると考えます。そして値が0にならなかった場合のみ2段階目へ進みます。ハードルをクリアしなければ次のステップに進めないというわけです。
2段階目では離散分布からのサンプリングが行われますが、このとき0は含みません。0を含まない離散分布からサンプリングするということですが、このような離散分布をゼロ切断分布と呼びます。理散分布はポアソン分布を仮定する場合が多いものの、カウントデータを扱えるものであれば特に制限はありません。なお、0を含まないポアソン分布は特に ゼロ切断ポアソン分布 と呼ばれています。
ハードルモデルに従うデータの例として、ここでは商品の購入個数が挙げられています。商品を購入するにあたって、まずそもそも購入するかどうかという意思決定のステップがあると考えます。これがハードルに相当します。購入すると決めたのであれば、少なくとも1つ以上の商品を購入するはずです。したがって購入個数はゼロ切断分布を想定するのが自然です。
ハードルモデルの特徴は0の中に第2ステップの離散分布に由来する0が含まれないという点です。0は純粋に第1ステップのベルヌーイ分布のみに由来するのです。
ゼロ過剰モデル
ゼロ過剰モデルでは、1段階目のステップとして離散分布からのサンプリングを行います。
第2ステップではベルヌーイ分布による選別を行い、一定の割合で値を0にします。
ハードルモデルと異なるのは、すべてのデータが両方のステップを通過するという点です。今回ステップの順序は重要でなく、入れ替えても結果は一緒です。重要なのは 離散分布からのサンプリング時に0を切断しない という点です。
結果として、0の中にはベルヌーイ分布により選別された0と、離散分布からたまたま選択された0が混ざることになります。
このことから分かるのは 離散分布から0の抽出される可能性が高いほど ハードルモデルとゼロ過剰モデルをきちんと区別する重要性は高くなるという点です。逆に、離散分布から0の抽出される可能性がほとんどなければ2つのモデルは似たような結果をもたらします(もちろん、解釈は異なるので区別することは大切です)。
ゼロ過剰モデルに従うデータの例として、こちらでは盗塁数が挙げられています。盗塁という行為は、そもそも試みる人と試みないがいると考えられます。しかし、盗塁を行う人でも必ずしも盗塁に成功するとは限りませんから、盗塁数0の中にはそもそも盗塁を行わない人と盗塁を試みたが盗塁できなかった人が混ざることになります。この場合は、先にベルヌーイ分布によるサンプリングを行ったと解釈できます。
先に離散分布からサンプリングをしたと考えられるような例として、こちら
ではふたたび商品の購入個数を挙げています。購入個数を決めたあとに、在庫切れなどによって強制的に購入個数が0になるようなケースではゼロ過剰モデルを想定したほうが自然といえます。
ゼロ過剰モデルにポアソン分布を組み合わせたモデルはよく使われているためか、ZIP(Zero-Inflated Poisson model)とも呼ばれます。
Rでゼロの多いカウントデータを扱う
Rでゼロの多いカウントデータを扱う方法はいくつかありますが、今回はハードルモデルとゼロ過剰モデルの両方を扱えるpsclパッケージを利用してみます。
psclではハードルモデルを扱うためのhurdle()関数とゼロ過剰モデルを扱うためのzeroinfl()関数が用意されており、利用方法はほぼ同じです。
基本的にはモデル式とデータを指定するだけで使えますが、多くの引数を用意しており、離散分布に負の二項分布を指定するようなことも簡単にできます。詳しくはパッケージのドキュメントを確認してください。
シミュレーション
psclを使用してハードルモデルとゼロ過剰モデルのパラメータ推定を実際にやってみたいと思います。
まずデータを生成します。今回は簡単のためにパラメータは切片のみ、つまりベルヌーイ分布の平均$\theta$とポアソン分布の平均$\lambda$のみを考えます。この2つのパラメータを指定すると、ハードルモデルとゼロ過剰モデルに従う2つのデータセットを生成するような関数を定義します。
set.seed(71)
gen_data <- function(theta, # ゼロになる確率
lambda, # ポアソン分布の平均
N = 1e5L # データ数
){
## ハードルモデルのデータ生成------------------------------
hurdle_d <- numeric(N)
for(i in seq_along(hurdle_d)){
## ハードルを超えるかどうか
if(rbinom(1L, 1L, 1 - theta) == 0L){
hurdle_d[i] <- 0L
} else {
## ハードルを超えたらゼロ切断ポアソン分布からサンプリング
tmp <- 0L
while(tmp == 0L){ tmp <- rpois(1L, lambda) }
hurdle_d[i] <- tmp
}
}
hurdle_d <<- data.frame(n = hurdle_d)
## ゼロ過剰ポアソン分布データの生成------------------------
zeroinfl_d <- numeric(N)
for(i in seq_along(zeroinfl_d)){
## まずサンプリング
tmp <- rpois(1L, lambda)
## 一定の確率で0に置き換える
if(rbinom(1L, 1L, 1 - theta) == 0L){ tmp <- 0L }
zeroinfl_d[i] <- tmp
}
zeroinfl_d <<- data.frame(n = zeroinfl_d)
}
まずは$\theta = 0.3$、$\lambda = 1.5$としてデータを生成します。
gen_data(theta = 0.3, lambda = 1.5)
可視化してみましょう。
library(ggplot2)
library(tidyr)
plot_data <- function(){
data.frame(
hurdle = hurdle_d$n,
zeroinfl = zeroinfl_d$n
) %>%
gather(key = model, value = n) %>%
ggplot(aes(x = n, fill = model)) +
geom_bar(position = "dodge", width = .5) +
theme_classic()
}
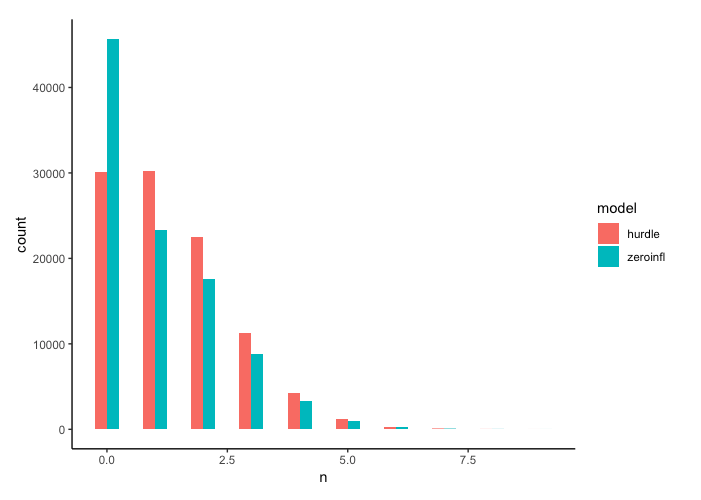
plot_data()
ゼロ過剰モデルには2種類のプロセスに由来する0が混ざるので、ハードルモデルより0が多くなっているのが分かります。
psclを使ってハードルモデルとゼロ過剰モデルのパラメータ推定を、モデル-データの組み合わせが正しい場合、正しくない場合で行ってみましょう。
library(pscl)
## Classes and Methods for R developed in the
## Political Science Computational Laboratory
## Department of Political Science
## Stanford University
## Simon Jackman
## hurdle and zeroinfl functions by Achim Zeileis
library(tibble)
library(purrr)
library(dplyr)
##
## Attaching package: 'dplyr'
## The following objects are masked from 'package:stats':
##
## filter, lag
## The following objects are masked from 'package:base':
##
## intersect, setdiff, setequal, union
library(rlist)
inv_logit <- function(x) 1 / (1 + exp(-x))
calc_coef <- function(){
tribble(
~funs, ~args,
## ハードルモデルをハードルモデルで解析
"hurdle", list(n ~ .|., hurdle_d),
## ハードルモデルをゼロ過剰モデルで解析
"zeroinfl", list(n ~ .|., hurdle_d),
## ゼロ過剰モデルをハードルモデルで解析
"hurdle", list(n ~ .|., zeroinfl_d),
## ゼロ過剰モデルをゼロ過剰モデルで解析
"zeroinfl", list(n ~ .|., zeroinfl_d)
) -> tmp
invoke_map(
tmp$funs,
tmp$args
) %>%
list.select(
count_coef = round(exp(coefficients$count), 3),
zero_coef = round(inv_logit(coefficients$zero), 3)
) %>%
list.stack() %>%
mutate(
pattern = c("d:hurdle m:hurdle",
"d:zeroinfl m:hurdle",
"d:hurdle m:zeroinfl",
"d:zeroinfl m:zeroinfl"),
count_coef,
zero_coef
)
}
calc_coef()
## count_coef zero_coef pattern
## 1 1.490 0.699 d:hurdle m:hurdle
## 2 1.490 0.098 d:zeroinfl m:hurdle
## 3 1.507 0.543 d:hurdle m:zeroinfl
## 4 1.507 0.302 d:zeroinfl m:zeroinfl
ポアソン分布のパラメータはいずれの場合でも正しく推定できましたが、ベルヌーイ分布のパラメータ推定はデータとモデルの組み合わせが正しくないと失敗してしまいます。また、ハードルモデルとゼロ過剰モデルでパラメータの意味が逆になっている点にも注意が必要です。ハードルモデルでは$\theta$は値が0ではない確率ですが、ゼロ過剰モデルでは値が0になる確率となっています。
なお、最初にも説明しましたが、離散分布から0があまり多くサンプリングされない場合、2つのモデルのもたらす結果はほぼ同じものになります。これはデータの生成プロセスを考えても自然な結果といえます。
試してみましょう。
gen_data(theta = 0.3, lambda = 5)
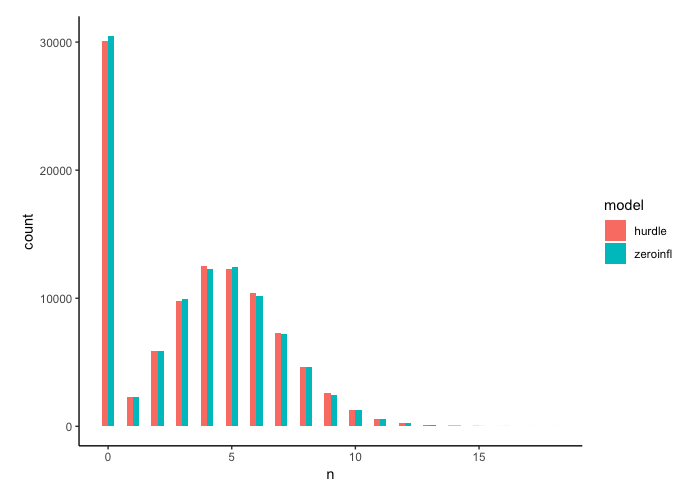
plot_data()
calc_coef()
## count_coef zero_coef pattern
## 1 5.014 0.699 d:hurdle m:hurdle
## 2 5.014 0.296 d:zeroinfl m:hurdle
## 3 4.998 0.695 d:hurdle m:zeroinfl
## 4 4.998 0.300 d:zeroinfl m:zeroinfl
このように、今回の例でいえば、$\lambda = 5$程度でもほとんど結果に違いが見られなくなります。とはいえデータの解釈が異なりますから、その点には注意が必要です。