統計の教科書の練習問題を解きながらRの使い方を学ぶ
「統計学入門 (基礎統計学Ⅰ) 」(東京大学教養学部統計学教室)の練習問題をRで解いていく。
第3章 2次元のデータ
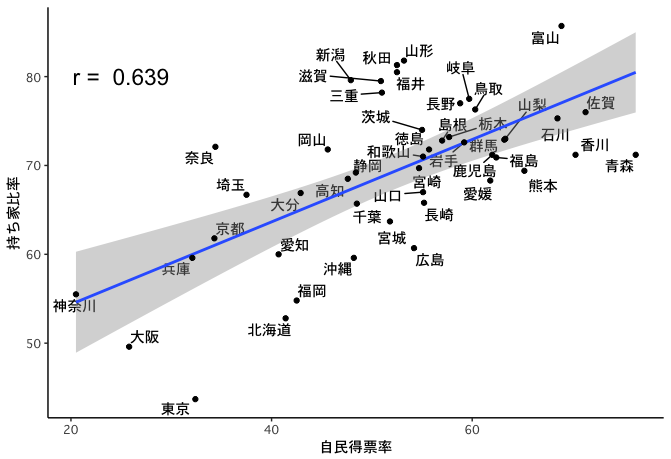
3.1 散布図を描け、そして相関係数を求めよ
この問題の一番むずかしい部分はデータの入力が面倒という点にある。変数名を考えるのも面倒だからバンバン日本語変数名を使うぞ。
pref <- c("北海道", "青森", "岩手", "宮城", "秋田", "山形", "福島", "茨城", "栃木",
"群馬", "埼玉", "千葉", "東京", "神奈川", "新潟", "富山", "石川", "福井",
"山梨", "長野", "岐阜", "静岡", "愛知", "三重", "滋賀", "京都", "大阪",
"兵庫", "奈良", "和歌山", "鳥取", "島根", "岡山", "広島", "山口", "徳島",
"香川", "愛媛", "高知", "福岡", "佐賀", "長崎", "熊本", "大分", "宮崎",
"鹿児島", "沖縄")
自民得票率 <- c(41.4, 76.3, 59.2, 51.8, 52.5, 53.2, 62.4, 55.0, 57.7,
63.2, 37.5, 48.5, 32.4, 20.5, 47.9, 68.9, 68.5, 52.5, 63.3, 58.8,
59.7, 48.4, 40.7, 51.0, 50.9, 34.3, 25.8, 32.1, 34.4, 55.1, 60.3,
57.0, 45.6, 54.2, 55.1, 55.7, 70.3, 61.8, 47.6, 42.5, 71.3, 55.2,
65.2, 42.9, 54.7, 62.0, 48.2)
持ち家比率 <- c(52.8, 71.2, 72.6, 63.7, 81.3, 81.8, 70.9, 74.0, 73.2,
72.9, 66.7, 65.7, 43.7, 55.5, 79.6, 85.7, 75.3, 80.5, 73.0, 77.0,
77.5, 69.2, 60.0, 78.2, 79.5, 61.8, 49.6, 59.6, 72.1, 71.0, 76.3,
72.8, 71.8, 60.7, 67.0, 71.8, 71.2, 68.3, 68.5, 54.8, 76.0, 65.8,
69.4, 66.9, 69.7, 71.2, 59.6)
d <- data.frame(pref, 自民得票率, 持ち家比率)
相関係数はcor()で求める。
r = cor(d$自民得票率, d$持ち家比率)
実際には回帰分析等を行ったほうが良いだろう。
> summary(lm(持ち家比率~自民得票率, data = d))
Call:
lm(formula = 持ち家比率 ~ 自民得票率, data = d)
Residuals:
Min 1Q Median 3Q Max
-16.4247 -4.4348 0.0489 3.8035 12.2884
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 45.10165 4.45919 10.114 3.64e-13 ***
自民得票率 0.46367 0.08325 5.569 1.35e-06 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 6.845 on 45 degrees of freedom
Multiple R-squared: 0.408, Adjusted R-squared: 0.3949
F-statistic: 31.02 on 1 and 45 DF, p-value: 1.354e-06
散布図を描くのはplot()一発だが、せっかくなのでggplot2を使いつつ、ggrepelでデータポイントにラベルをつけよう。
library(ggplot2)
library(ggrepel)
ggplot(d, aes(x = 自民得票率, y = 持ち家比率)) +
geom_text_repel(
aes(label = pref),
family = "Osaka" # macOS向け
) +
geom_smooth(method = lm) +
geom_point() +
annotate(geom = "text",
x = 25, y = 80,
label = paste("r = ", round(r, 3)),
size = 6) +
theme_classic(base_family = "Osaka") + # macOS向け
theme(legend.position = "none")
ggplot2ではプロット用データとしてデータフレームを用いる。ggplot()関数にデータフレームを与えたら、さらにaes()関数でどの列をどの要素に対応付けるかを指定する。この例ではxに自民得票率を、yに持ち家比率を対応させている。
ここに主にgeom_***()という名前の関数を「足す」ことでグラフの種類を変更したり、足したり、theme_***()という名前の関数を足すことで外観を調整したりする、というのがggplot2を利用する際の描画の流れになる。
geom_text_repel()はデータポイントにラベルを付けることの出来る要素だが、ラベル同士が「反発する(repulsive)」かのようにうまく重ならない位置に配置され、要素数が多くなっても可読性が落ちにくい。ここではラベル情報を利用するために、aes()でラベルとprefを新しく関連付けている。また、familyでフォントを指定しているが、ggplot2では日本語がしばしば文字化けするという点を覚えておくと良い。後述のtheme_***()の中で指定することで事足りる場合もあるが、geom_text_repelのように個別の指定が必要となる場合も多い。
geom_smooth()は平滑線を、geom_point()は散布図を追加する。geom_smooth()ではmethod=引数によって平滑化手法を指定している点にも注意してもらいたい。ggplot2ではこのように「ついでに計算する」機能が結構たくさんある。ただ、個人的には「思ったよりはずっとできる」が「あまり細かいことをやろうとすると逆に苦労する」印象。
annotate()は元のデータとは関係なく色々な情報、図形を図中に追加できる。ここでは事前に計算しておいたrの値を利用している。
theme_***()はプロットの外観(theme)をざっくりと変更する。大域的なフォントの指定はここで行う。
theme()はより細かく要素を調整する。ここではデフォルトで表示されてしまう凡例を非表示に設定している。
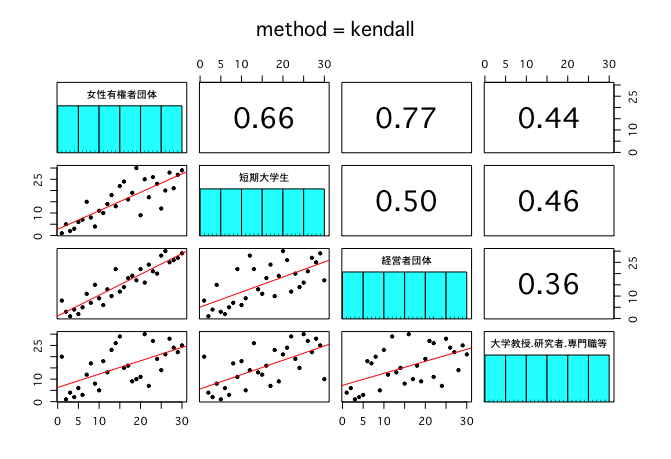
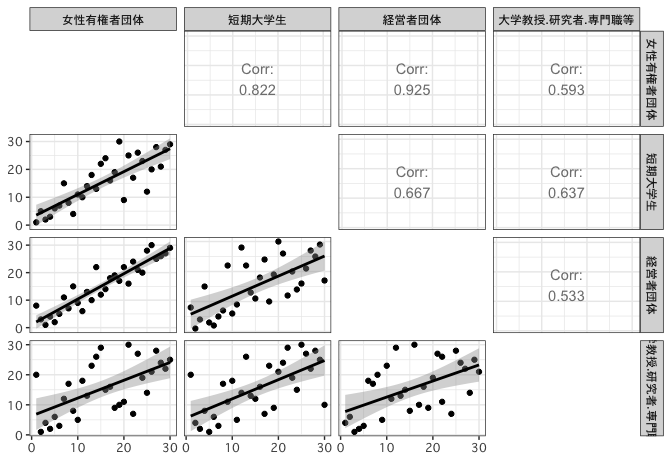
3.3 2つのグループについてスピアマン、ケンドールの順位相関係数をそれぞれ求めよ
相関係数はcor()で求めるが、このときデータフレームを与えると相関行列を返してくれる。またmethod=引数で計算方法を指定できる。
d <- data.frame(
"女性有権者団体" = 1:30,
"短期大学生" = c(1, 5, 2, 3, 6, 7, 15, 8, 4, 11, 10, 14, 18, 13,
22, 24, 16, 19, 30, 9, 25, 17, 26, 23, 12, 20, 28, 21, 27, 29),
"経営者団体" = c(8, 3, 1, 4, 2, 5, 11, 7, 15, 9, 6, 13, 10, 22, 12, 14, 18, 19,
17, 22, 16, 24, 21, 20, 28, 30, 25, 26, 27, 29),
"大学教授、研究者、専門職等" = c(20, 1, 4, 2, 6, 3, 12, 17, 8, 5, 18, 13, 23, 26, 29, 15, 16,
9, 10, 11, 30, 7, 27, 19, 14, 21, 28, 24, 22, 25)
)
cor(d, method = "spearman")
cor(d, method = "kendall")
> cor(d, method = "spearman")
女性有権者団体 短期大学生 経営者団体 大学教授.研究者.専門職等
女性有権者団体 1.0000000 0.8215795 0.9249082 0.5933259
短期大学生 0.8215795 1.0000000 0.6668150 0.6373749
経営者団体 0.9249082 0.6668150 1.0000000 0.5326510
大学教授.研究者.専門職等 0.5933259 0.6373749 0.5326510 1.0000000
> cor(d, method = "kendall")
女性有権者団体 短期大学生 経営者団体 大学教授.研究者.専門職等
女性有権者団体 1.0000000 0.6643678 0.7687002 0.4390805
短期大学生 0.6643678 1.0000000 0.5017265 0.4620690
経営者団体 0.7687002 0.5017265 1.0000000 0.3590336
大学教授.研究者.専門職等 0.4390805 0.4620690 0.3590336 1.0000000
これだけでは面白くないのでプロットしてみよう。方法はいくつかあるが、psychパッケージのpairs.panels()関数が比較的手軽(順位相関係数だと対角部分のヒストグラムが余分だけど消す方法がわからなかった)。
library(psych)
par(family = "Osaka") # mac用
pairs.panels(d, method = "spearman", lm = TRUE, ellipses = FALSE, density = FALSE, main = "method = spearman")
pairs.panels(d, method = "kendall", lm = TRUE, ellipses = FALSE, density = FALSE, main = "method = kendall")
GGallyパッケージのggpairs()を使うという手もある。
library(GGally)
ggpairs(d,
diag = "blank",
upper = list(continuous = wrap("cor", method = "spearman")),
lower = list(continuous = wrap("smooth"))) +
theme_bw(base_family = "Osaka") # mac用
対角部分、上三角部分、下三角部分をそれぞれカスタマイズ可能だが、指定の仕方に多少癖がある。
3.4
i) [1,11]の範囲で整数の乱数を発生させよ
sample()は第一引数に抽出対象のベクトルを指定するが、ベクトルの代わりに単一の整数xを指定すると、自動的に抽出対象が1:xに置き換えられる。
さらに、第二引数に指定する抽出サイズも省略すると、xが自動的に使われる。
乱数の発生源として使う場合はreplace = TRUEを指定して復元抽出としておくことを忘れずに。
sample(11, 100, rep = TRUE) # 100個の乱数
sample(11, rep = TRUE) # 11個の乱数
ii) 乱数に基づいてデータを11回抽出し、11個の相関係数を計算せよ
同じ関数を繰り返して使用する場合はreplicate()を使う。結果がベクトルで返ってくる。
d <- data.frame( # 元データ
x = c(71, 68, 66, 67, 70, 71, 70, 73, 72, 65, 66),
y = c(69, 64, 65, 63, 65, 62, 65, 64, 66, 59, 62)
)
cor_d <- function(df) cor(df[[1]], df[[2]])
replicate(11, cor_d(d[sample(11, rep = TRUE), ]))
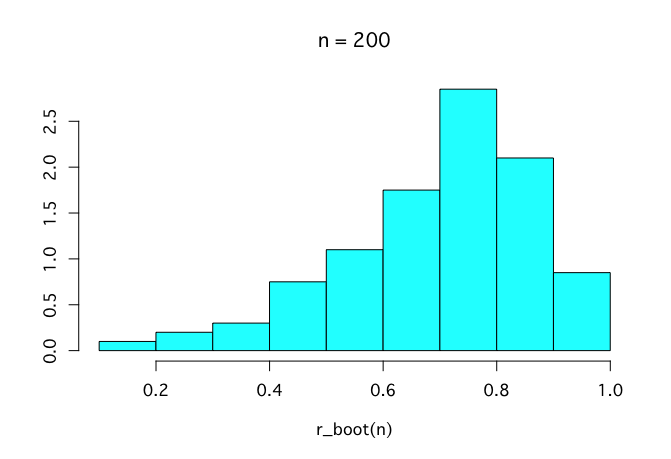
iii) 先程の手順を200回繰り返せ
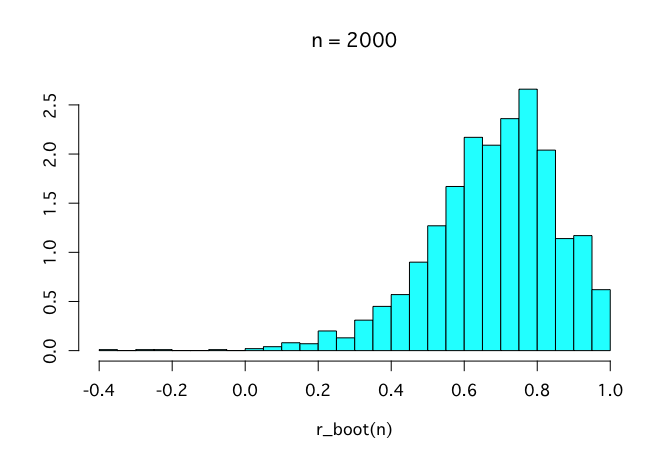
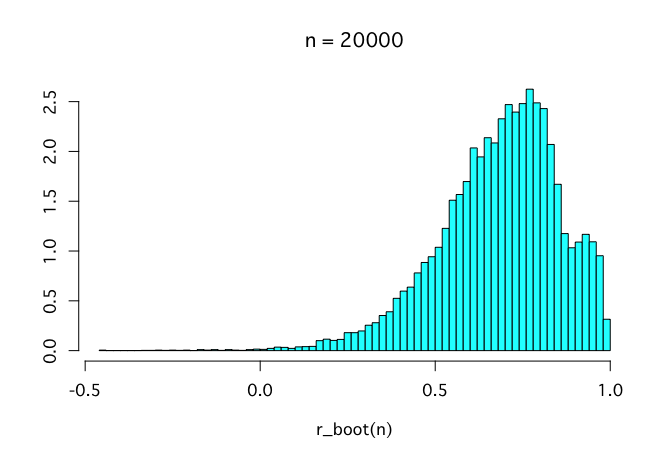
200回と言わず2万回くらい繰り返してみよう。これくらい繰り返すときれいなヒストグラムが描ける。
# 繰り返す関数
r_boot <- function(n) replicate(n, cor_d(d[sample(11, rep = TRUE), ]))
# ヒストグラムを描く関数
r_truehist <- function(n) MASS::truehist(r_boot(n))
r_truehist(200)
r_truehist(2000)
r_truehist(2e4)
また、得られたブートストラップサンプルから信頼区間の信頼区間を求めることができる。パーセンタイル法で求めるなら、quantile()を使う。元の相関係数とブートストラップサンプルの中央値や平均値、cor.test()で求められる95%信頼区間なども合わせて確認してみよう。
rb <- r_boot(2e4)
quantile(rb, p = c(0.025, 0.5, 0.975))
mean(rb)
cor.test(d$x, d$y)
それぞれ似たような値にはなるが同じにはならない。
> quantile(rb, p = c(0.025, 0.5, 0.975))
2.5% 50% 97.5%
-0.005369111 0.573268329 0.890707111
> mean(rb)
[1] 0.5392091
> cor.test(d$x, d$y)
Pearson's product-moment correlation
data: d$x and d$y
t = 2.0175, df = 9, p-value = 0.07442
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
-0.06286527 0.86751705
sample estimates:
cor
0.5580547
今回はbaseでプロットしてみよう。baseの場合はひたすら描きたい要素を積み重ねていく。一つづつ確認しながらやりやすい反面、あとで細かい部分を修正しようとすると割と面倒だったりする。
plot(density(rb))
abline(v = quantile(rb, p = c(0.025, 0.975)), col = "grey")
abline(v = cor.test(d$x, d$y)$conf.int, col = "green")
abline(v = quantile(rb, p = 0.5), col = "red")
abline(v = cor(d$x, d$y), col = "black")
abline(v = mean(rb), col = "blue")
legend("topleft", inset = 0.05,
legend = c("median(b)", "r", "mean(b)", "95%C.I.(b)", "95%C.I.(cor.test)"),
col = c("red", "black", "blue", "grey", "green"),
lty = 1,
box.lty = 0)
ついでにStanでも相関係数を求めてみよう。データは二変量正規分布に従うと仮定する。
まず、cor.stanというファイル名で下記の内容を保存しておく。
data {
int N;
vector[2] y[N];
}
parameters {
vector[2] mn;
cov_matrix[2] cov;
}
model {
for (n in 1:N)
y[n] ~ multi_normal(mn, cov);
}
generated quantities {
real cor;
cor = cov[1,2] / (sqrt(cov[1,1] * cov[2,2]));
}
R側。
# install.packages("rstan")
library(rstan)
rstan_options(auto_write = TRUE)
options(mc.cores = parallel::detectCores())
model <- stan_model("cor.stan")
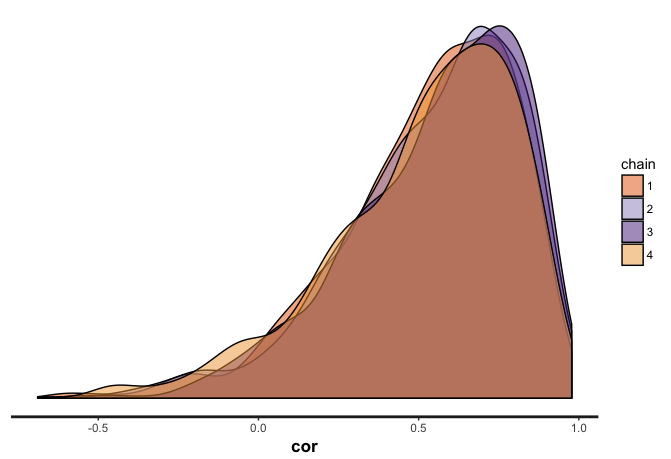
fit <- sampling(model, data = list(N=11, y=as.matrix(d)))
print(fit, pars = "cor")
だいたい似たような推定値になった。
> print(fit, pars = "cor")
Inference for Stan model: cor.
4 chains, each with iter=2000; warmup=1000; thin=1;
post-warmup draws per chain=1000, total post-warmup draws=4000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
cor 0.54 0.01 0.27 -0.12 0.38 0.59 0.75 0.91 2235 1
Samples were drawn using NUTS(diag_e) at Wed Jul 26 21:34:51 2017.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at
convergence, Rhat=1).
plot(fit, pars = "cor")
stan_dens(fit, pars = "cor", separate_chains = TRUE)
第4章 確率
4.1 <ド・メレの問題>
i) サイコロを4回なげたとき、6の目が一度も出ない確率は
計算とシミュレーションの2通りで求めてみよう。同じ思考を繰り返すのであればreplicate()が便利だ。指定回数の繰り返しの結果をベクトル(または行列、配列)で返してくれるので、それを集計すれば良い。
> ## 計算
> (5/6)^4 # 1回も6の目がでない
[1] 0.4822531
>
> ## シミュレーション
> n <- 1e5 # 試行回数
> result <- replicate(n, 6 %in% sample(6, 4, rep=TRUE)) # 1回でも6が出たらTRUE
> 1 - (sum(result) / n) # 1回も6の目が出ない
[1] 0.48201
ii) 2つ同時に24回投げたときに(6, 6)が一度も出ない確率は
## 計算
(35/36)^24 # 1回も(6, 6)が出ない
## シミュレーション
n <- 1e5
try <- function(){ # 試行:1回でも(6, 6)が出たらTRUE
"6 6" %in% apply(matrix(sample(6, 24*2, rep = TRUE), ncol = 2),
1, paste, collapse = " ")
}
1 - (sum(replicate(n, try())) / n)
apply()とpaste()を同時に使う場合、collapse=を指定しないと思ったような結果にならない。この挙動が正しいのかどうかよく分かっていない。
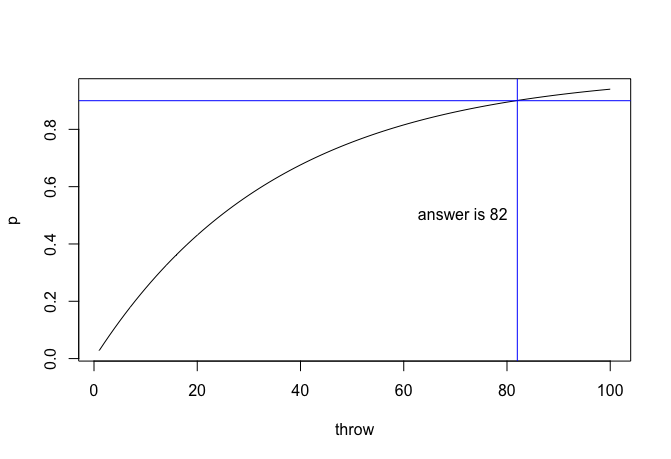
4.2 2つのサイコロを何回投げれば少なくとも1回は出目の和が12になる確率が0.9を超えるか。
throw_dices <- function(n) { 1 - (35/36)^n } # n回投げたときに1回は和が12になる確率
plot(throw_dices(1:100), type = "l", # 投げた回数 vs 確率のグラフ
xlab = "throw", ylab = "p")
abline(h = 0.9, col = "blue") # p = 0.9の部分にライン
answer <- min((1:100)[throw_dices(1:100) > 0.9]) # p=0.9以上となる最少の試行回数
abline(v = answer, col = "blue")
text(x = answer, y = 0.5,
label = paste("answer is", answer),
pos = 2)
4.3 30人のなかから15人を選ぶ組み合わせの総数は?
$$
{30 \choose 15}
$$
choose()という関数がある。
> choose(30, 15)
[1] 155117520
ところで、choose()では扱える桁に限度がある。
> choose(300, 150)
[1] 9.37597e+88
そんなときはgmpパッケージのchooseZ()関数を使おう。
> gmp::chooseZ(300, 150)
Big Integer ('bigz') :
[1] 93759702772827452793193754439064084879232655700081358920472352712975170021839591675861424
4.4 r人の中に同じ誕生日の人間が少なくとも居る確率を示せ
なお閏年は考慮しない。
sapply(X, FUN)はベクトルXにFUNをそれぞれ適用した結果をベクトルで返す。
> pr = function(r){
+ sapply(r, function(x) {1 - prod(1-1:(x-1)/365)})
+ }
> r <- c(5, 10, 15, 20:25, 30, 35, 40, 50, 60)
> data.frame(r, p = pr(target))
r p
1 5 0.02713557
2 10 0.11694818
3 15 0.25290132
4 20 0.41143838
5 21 0.44368834
6 22 0.47569531
7 23 0.50729723
8 24 0.53834426
9 25 0.56869970
10 30 0.70631624
11 35 0.81438324
12 40 0.89123181
13 50 0.97037358
14 60 0.99412266
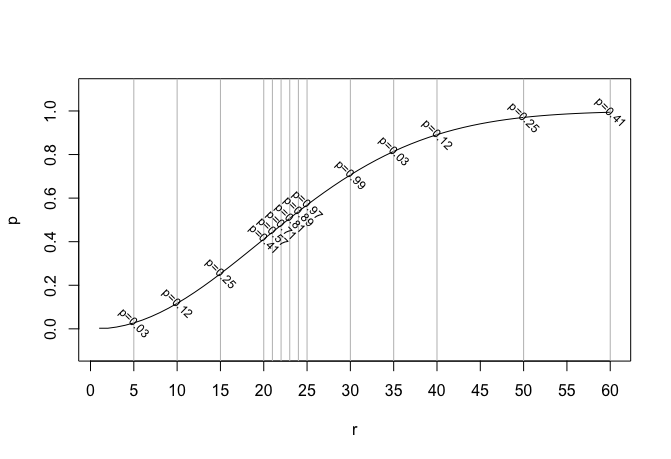
プロットしておこう。
plot(pr(1:60), type = "l", ylim = c(-0.1, 1.1), axes = 0,
xlab = "r", ylab = "p")
axis(1, at = seq(0, 60, by = 5))
axis(2)
box()
abline(v = r, col = "gray")
rn <- rn <- r[!(r %in% 21:24)]
text(x = r, y = pr(r),
labels = paste0("p=", round(pr(rn), 2)),
srt = -45,
cex = 0.75)
4.7 ベイズの公式
i)
$\mathrm{P}(A|C) = \mathrm{P}(A^c|C^c) = 0.95$かつ$\mathrm{P}(C) = 0.005$のとき、$\mathrm{P}(C|A)$を求めよ。
> (0.005 * 0.95) / (0.005 * 0.95 + 0.995 * 0.05)
[1] 0.08715596
ii)
$\mathrm{P}(A|C) = \mathrm{P}(A^c|C^c) = R$($0<R<1$)としたとき、$\mathrm{P}(C|A) \geqq 0.90$となるために必要な$R$を求めよ。
optimize()は与えられた関数を最大化または最小化するので、逆関数を近似的に求めるのに使うことができる。uniroot()でも同様のことができる。
> optimize(function(x){abs(0.9 - p_CA(x))}, lower = 0, upper = 1)
$minimum
[1] 0.9994283
$objective
[1] 0.002202983
> uniroot(function(x){0.9 - p_CA(x)}, interval = c(0, 1))
$root
[1] 0.9994322
$f.root
[1] 0.001569955
$iter
[1] 6
$init.it
[1] NA
$estim.prec
[1] 6.103516e-05
第5章 確率変数
5.1 <一様分布> いくつかの一様分布に対して、次の計算を行え。
i) [0, 6]上の一様分布の密度関数、期待値、分散
密度関数
[0, 6]上で確率密度が等しいので、
$$
f(x) = \left\{
\begin{array}{ll}
1/6 & (0 \le x \le 6のとき) \\
0 & (それ以外)
\end{array} \right.
$$
一般に、[α, β]上の一様分布の密度関数は$\frac{1}{\beta - \alpha}$となる。
期待値
$$
E(x) = \int_{-\infty}^{\infty}xf(x)dx \\
= \int_0^6x\frac{1}{6}dx \\
= \frac{1}{6}\left[\frac{1}{2}x^2\right]_0^6 \\
= 3
$$
おっとRを使うのだった。定積分はintegrate()で行う。
f <- function(x) x * 1/6
integrate(f = f, lower = 0, upper = 6)
## 3 with absolute error < 3.3e-14
分散
以下の関係を使う。
$$
V(x) = E(x^2) - E(x)^2
$$
$$
E(x^2) = \int_0^6 x^2\frac{1}{6}dx \\
= \frac{1}{6}\left[\frac{1}{3}x^3\right]_0^6 \\
= 12
$$
より、
$$
V(x) = 12 - 9 = 3
$$
おっとRを使うのであった。integrate()の結果はintegrateクラスのオブジェクトになっており、積分値には$valueスロットを通じてアクセスする。
f2 <- function(x) (x - integrate(f, lower = 0, upper = 6)$value)^2 * 1/6
integrate(f2, lower = 0, upper = 6)
## 3 with absolute error < 3.3e-14
ii) 同じく、チェビシェフの不等式の成立
チェビシェフの不等式とは、確率変数Xの期待値をμ、標準偏差をσ2としたとき、一般に成立する以下の不等式を指す。
$$
P(|X-\mu| \ge k \sigma) \le 1/k^2
$$
言葉で説明すれば、「平均からk**σ以上離れた値が出る確率は1/k2以下である」ということだ。
さて、今回の例では、μ = 3、$\sigma = \sqrt{\sigma^2} = \sqrt{3^2}$である。
平均からk**σ以上離れた値が出る確率は、
$$
\int_{3+k\sqrt{3}}^{\infty} x \frac{1}{6}dx + \int_{-\infty}^{3-k\sqrt{3}}x\frac{1}{6}dx = \\
1 - \int_{3-k\sqrt{3}}^{3+k\sqrt{3}}x\frac{1}{6}dx = \\
1 - \frac{1}{6}\left[\frac{1}{2}x^2\right]_{3-k\sqrt{3}}^{3+k\sqrt{3}} = \\
1 - k\frac{\sqrt{3}}{3}
$$
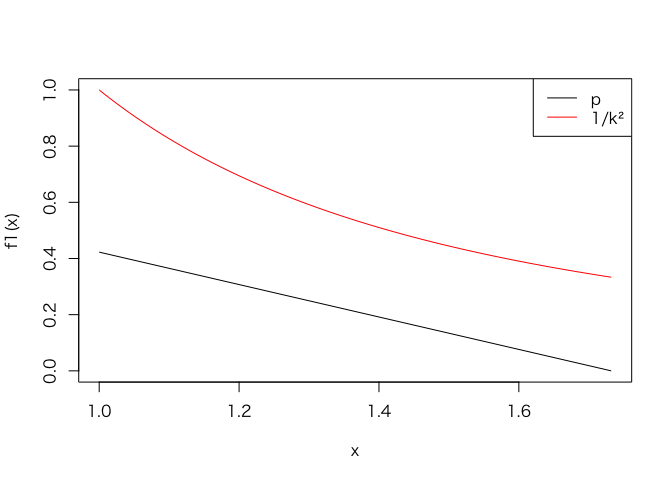
なんかこの先難しくて証明できなかったのでプロットして確認してみよう。$1 \le k \le \sqrt{3}$なので、この区間だけ確認すれば良い。
f1 <- function(k) 1-k*sqrt(3)/3
f2 <- function(k) 1/k^2
curve(f1, 1, sqrt(3), ylim = c(0, 1))
curve(f2, 1, sqrt(3), add = TRUE, col = "red")
legend("topright", legend = c("p", "1/k²"), col = 1:2, lty = 1)
ii) [0, 1]上の一様分布の歪度、尖度
歪度
歪度は
$$
\alpha_3 = E(X-\mu)^3/\sigma^3
$$
と定義される。平均値のまわりの3次モーメントとも言う。[0, 1]上の一様分布は平均1/2、分散1/12なので、
$$
E(X-1/2)^3/(1/12)^{3/2}
$$
X − 1/2 = Tと置くと、期待値部分は
$$
\int_{-1/2}^{1/2}t^3dt
$$
となるので答えは明らかに0なのだが(そもそも歪度の名前が示すとおり、歪みの程度を示す指標なので答えが0になるのは当然だ)、一応Rで計算してみよう。
f <- function(x) (x-1/2)^3
integrate(f, 0, 1)$value / (1/12)^(3/2)
## [1] 5.481456e-17
尖度
尖度は平均値のまわりの4次モーメント、
$$
\alpha_4 = E(X-\mu)^4/\sigma^4
$$
から3を引いたものだ。3は正規分布のα4であり、要するに正規分布と比較して尖っているのか平らなのかを比べる指標である。
$$
E(X - 1/2)^4 / (1/12)^2 = 9/5
$$
なので、3を引くと-6/5となる。
f <- function(x) (x-1/2)^4
integrate(f, 0, 1)$value / (1/12)^2 - 3
## [1] -1.2
ところで歪度と尖度はmomentsパッケージのskewness()、kurtosis()関数で計算できる(同様の関数はe1071パッケージにもある)。一様分布に従う乱数を発生させて歪度と尖度を計算してみよう。
library(moments)
x = runif(1e6)
skewness(x)
## [1] -0.001229028
kurtosis(x)
## [1] 1.798193
kurtosis()の結果がほぼ1.8になっているが、これは3を引いていないためだ。尖度の定義はこのように3を引かないものもあるので注意する必要がある。
5.2 <期待値の実地例> 5.2節の宝くじの期待値を求めよ
ここでいう「宝くじ」は1300万通りの宝くじに対して以下の通り当選金と本数が設定されているようなものである。
library(dplyr)
##
## Attaching package: 'dplyr'
## The following objects are masked from 'package:stats':
##
## filter, lag
## The following objects are masked from 'package:base':
##
## intersect, setdiff, setequal, union
options(scipen=10)
x <- c(4e7, 1e7, 2e5, 1e7, 1e5, 1e6, 14e4, 1e4, 1e3, 2e2)
n <- c(7, 14, 903, 5, 645, 130, 130, 1300, 26000, 1300000)
data.frame(
当選金 = round(x),
本数 = n
) %>% knitr::kable()
| 当選金 | 本数 |
|---|---|
| 40000000 | 7 |
| 10000000 | 14 |
| 200000 | 903 |
| 10000000 | 5 |
| 100000 | 645 |
| 1000000 | 130 |
| 140000 | 130 |
| 10000 | 1300 |
| 1000 | 26000 |
| 200 | 1300000 |
x <- c(4e7, 1e7, 2e5, 1e7, 1e5, 1e6, 14e4, 1e4, 1e3, 2e2)
n <- c(7, 14, 903, 5, 645, 130, 130, 1300, 26000, 1300000)
sum(x * n) / 13e6
## [1] 89.40769
5.3 <聖ペテルブルグの逆説>
コインを繰り返し投げ、はじめて表が出た時に止める。それがn回目であるとき、2ⁿ円を得るものとする。
i) 得られる額Xの確率分布を求めよ
$$p(X = 2^n)=1/2^n$$
ii) E(X)は存在しない(∞である)ことを示せ
$$
E(X) = \sum_{n=0}^\infty 2^n \frac{1}{2^n} = \infty
$$
5.4 <最小平均二乗>
E(X − a)2を最小にするaおよびその最小値を求めよ。
$$
E(x-a)^2 = E(x^2 -2ax + a^2) \\
= E(x^2) - 2aE(x) + a^2
$$
aについて下に凸の関数となっているので、微分して0とおく。
$$
0 = 2a − 2E(x)
$$
$$\therefore a =E(X)$$
5.5 <正n面体から発生する乱数>
正n面体で1, 2, ..., nの乱数を発生させるとする。この乱数の期待値、分散を求めよ。ただし、正n面体とは正4, 6, 8, 12, 20面体の5種類の立体のことである。
期待値
$$
E(x) = \sum_{x=1}^n x \frac{1}{n} \\
= \frac{n+1}{2}
$$
分散
$$
V(x) = E(x^2) - E(x)^2 \\
= \sum_{x=1}^n x^2 \frac{1}{n} - \left(\frac{n+1}{2}\right)^2 \\
= \frac{(2n+1)(n+1)}{6} - \frac{(n+1)^2}{4}
= \frac{n^2-1}{12}
$$
5.6 < 一様分布の平方変換>
- 確率変数Xが[0,1]上の一様分布に従う時、X²の累積分布関数、密度関数、期待値、分散を求めよ。
確率変数Xを単調増加の関数ϕによってYに変換するとする。このとき、(x, x + Δ**x)が(y, y + Δ**y)へ移るが、このとき
P(x ≤ X ≤ x + Δ**x)=P(y ≤ Y ≤ y + Δ**y)
であるので、XとYの確率密度関数をそれぞれf(x)、g(y)とすれば
f(x)Δ**x = g(y)Δ**y
となり、従って
$$
g(y) = f(x)\frac{\Delta x}{\Delta y} \approx f(x)\frac{dx}{dy}
$$
ここでx = ψ(y)となる関数ψを考えれば、
$$
g(y) = f(\psi(y)) \frac{d(\psi(y))}{dy}
$$
問題はX2の確率分布について考えるというものだったので、これをYとおく。x2 = yより$x = \sqrt{y}$であるので、密度関数は以下のように表すことができる。f(⋅)=1に注意してほしい。
$$
g(y) = f(\sqrt{y})\frac{d\sqrt{y}}{dy} = \frac{1}{2\sqrt{y}}
$$
また、これより累積分布関数は
$$
Y = \sqrt{y}
$$
となる。期待値は
$$
E(X^2) = \int_0^1 x^2 dx = \frac{1}{3}
$$
分散は
$$
V(X^2) = E(X^4) - E(X^2)^2 \\
= \int_0^1 x^4 dx - \frac{1}{9} \\
= \frac{1}{5} - \frac{1}{9} \\
= \frac{4}{45}
$$
5.7 <正規分布の平方変換>
- 確率変数Xが、μ = 0、σ = 1の正規分布に従うとき、X2の累積分布関数、密度関数、期待値、分散を求めよ。
5.6と逆の方向(テキストに載っている方)でやる。
まず、標準正規分布の−∞からxまでの積分を
$$
\Phi(x) = \int_{-\infty}^x \frac{1}{\sqrt{2\pi}}\exp{\frac{-u^2}{2}}du
$$
とおく。
$$
F(y) = P(X^2 \le y) = 2P(0 \le X \le \sqrt{y}) = 2(\Phi(\sqrt{y})-1/2)
$$
途中で2倍しているのはy = x2よりyの定義域が[0, ∞]となるためで、最後に引いている1/2はΦ(0)である。
累積分布関数を微分すれば確率密度関数が得られるので、
$$
f(y) = 2\Phi'(\sqrt{y})\frac{1}{2\sqrt{y}} \\
= \frac{\exp (-\frac{y}{2})}{\sqrt{2\pi y}}
$$
となる。
平均と分散は難しいのでインチキをすると、
- 平均E(X2)は標準正規分布の分散に等しいので、E(X2)=V(X)=1。
- 分散はV(X2)=E(X4)−1となるが、E(X4)は標準正規分布の尖度に等しいのでV(X2)=3 − 1 = 2。
5.8は見たままなので略。