このコードについて、twitter上で「Juliaなら数十秒で終わるのにRだとめっちゃ時間かかったんだろうな…」的な発言が流れてきたのを見かけて、本当にそうなのか気になったので少し調べました。
そもそもRのループは遅いのか?
たしかに、Rのforループが非常に遅いとされていた時代はありました。繰返し処理はなるべくベクトル化して書くべきものであって、forを書くというのは可能であれば避けるべき作法でした。
しかし、R 3.4.0からJITコンパイラが同梱されており、これがデフォルトでONになっている恩恵で、現代のRのforループの速度は相当に改善されています。場合によってはforを書いたほうが速度的に有利なことすらあります。
やってみる
まあともかくやってみましょう。
実測とプロファイリング
まず「そもそも元のコードがどれだけ時間がかかるのか」を確認しておくと、私の手元のちょっと古くなってきたMac mini (Late 2012, 2.3 GHz Intel Core i7)だと4分くらいでした。
Juliaが数十秒で終わるのであれば(後で確認します)、確かに時間がかかっていると言えそうです。
sample()やifelse()が実際には不要であるとか、多少のリファクタリングの余地はあるものの、おそらくこれは速度に対して本質的な部分ではありません。なので、まずはなるべく元のコードを尊重して話を進めることにします。
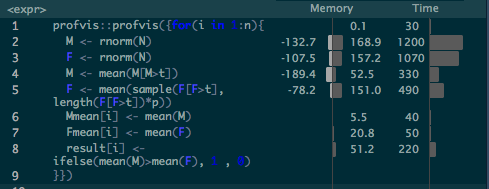
どこが遅いのかを確認するには、RStudioのProfile機能を使うと便利です。コードの調べたい部分を選択して「Profile > Profile Selected Line(s)」を実行するとプロファイリングが行われます。結果は次のようになります(調査のためループ回数は減らしてあります)。
結果から明らかなように、rnorm()がかなり重たい処理のようです。逆に言えば、ここさえ高速化できれば速度改善が見込めそうです。
dqrngパッケージを使う
dqrngパッケージは、高速な疑似乱数の生成を可能にするパッケージです。このパッケージではpcg64、Xoroshiro、Threefryといった乱数生成器がサポートされており、デフォルトではこの中で最速のXoroshiro128+が採用されています。XoroshiroはXorshiftの変種で、統計的性質についてメルセンヌ・ツイスタよりも優れた部分もあるようです(cf. xoshiro/xoroshiro generators and the PRNG shootout)。
各関数の利用方法はRの標準の乱数生成関数とほぼ同じです。「rnorm()に対応する関数はdqrnorm()である」といった具合に頭にdqが付いたものがdqrng版の関数になっています。ただ、現時点では対応している関数はまだ多くありません。
パッケージはCRANからもインストールできますが、今回はsample()のdqrng版であるdqsample()も使いたいので、開発版をインストールします。開発版のインストールはdratパッケージを使う方法が推奨されているようです。
if (!requireNamespace("drat", quietly = TRUE)) install.packages("drat")
drat::addRepo("daqana")
install.packages("dqrng")
で、元のコードをdqrngパッケージを使うように修正しました。具体的には、次の修正を行っただけです。軽微な変更なのでコードの提示は省略します。
-
library(dqrng)を追加 -
rnormをdqrnormに変更 -
sampleをdqsampleに変更
結果、実行時間は次のようになりました。
単にdqrngパッケージを使うだけで、実行時間を約6割短くすることができました。しかしまだ100秒かかっているので「数十秒」と言うにはチョット辛いところです。
少しリファクタリングする
もう少し速度を追ってみたいと思うので、コードを整理してみます。具体的には、はじめに少し触れたようにsample()とifelse()が結果に対して不要なので、これを取り除きます。
変更箇所だけ示すとこうです。
for (i in seq_len(n)) {
M <- dqrnorm(N)
F <- dqrnorm(N)
f <- F[F > t]
Mmean[i] <- mean(M[M > t])
Fmean[i] <- mean(f[1:(length(f) * p)])
}
resultという変数で計算していた部分はsum(Mmean > Fmean, na.rm = TRUE)で計算できます。
で、結果はこうです。
元の状態から8割程度の実行時間削減ができました。もう「数十秒」と言って良いような気もします。
Juliaはどうなのか
問題はこちらです。
Juliaで書いてみる
次のようなコードを書きました。
using Statistics
using DataFrames
using Gadfly
n = 1000000
N = 1000
p = 0.3
t = 2
function mfmean()
M = randn(N)
F = randn(N)
f = F[F .> t]
Mmean = mean(M[M .> t])
Fmean = mean(f[1:Int(round(length(f)*p))])
return DataFrame(
category = ["Mmean", "Fmean"],
value = [Mmean, Fmean]
)
end
@time result = vcat([mfmean() for i in 1:n]...)
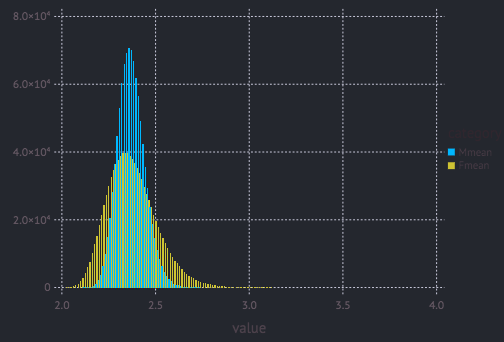
plot(result, x = "value", color = "category", Geom.histogram(bincount = 120, position = :dodge))
プロットはきれいに書けたので結果は間違ってないと思います。
あまり手を加えなくても格好良く出力されて良いですね。ちなみにAtomにJunoを入れて書きました。使いやすかったです。
肝心の@timeで計測した部分ですが、次のような結果になりました。
118.985376 seconds (91.30 M allocations: 28.143 GiB, 38.38% gc time)
遅いです。数十秒どころではないです。Rの完全勝利…?
ただ、この結果は結構怪しいと思っていて、なぜなら私はJuliaのコードを書き慣れていないからです。Juliaのコードは少し手を加えると劇的に高速化されることがよくあるので、上記のコードにもそういう部分がありそうな気がしています。詳しい方からのご指摘お待ちしております。
乱数生成とループ部分だけを比較する
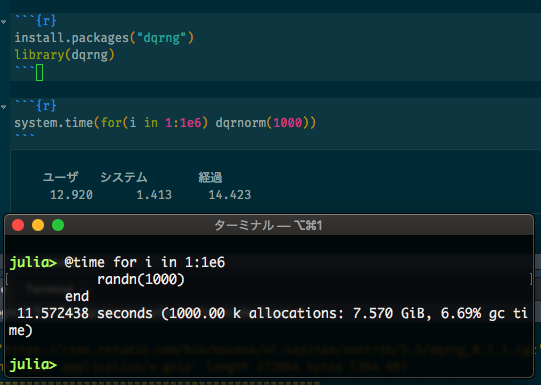
私の適当なコードで速度比較するのも公平性に欠けるので、乱数生成とループの部分だけに注目して比較してみました。
Juliaの方が少し早いという結果になりました。ただ、Juliaもデフォルトでは乱数生成にメルセンヌ・ツイスタを使用しているようなので(Random Numbers · The Julia Language)、その点を加味すればやはりJuliaは相当早いということが言えそうです。Rでrnorm()を使った場合は次のような結果になります。
やはりメルセンヌ・ツイスタ同士ではかなりの差が出ます。
きちんと調べていませんが、JuliaでXoroshiro128+を使うようにすれば相当な速度が出るのかもしれません。
Julia再チャレンジ
(2019-04-18 21:00追記)
詳しい方からのご指摘が集まってきたので書き直してみました。
using Statistics
using DataFrames
using RandomNumbers.Xorshifts
const XOROSHIRO128PLUS = Xoroshiro128Plus()
function mfmeans(n)
N = 1000
p = 0.3
t = 2
Mmeans = Vector{Float64}(undef, n)
Fmeans = Vector{Float64}(undef, n)
for i = 1:n
M = randn(XOROSHIRO128PLUS, N)
F = randn(XOROSHIRO128PLUS, N)
f = F[F .> t]
Mmeans[i] = mean(M[M .> t])
Fmeans[i] = mean(f[1:round(Int, length(f)*p)])
end
return DataFrame(
category = [repeat(["Mmean"], n); repeat(["Fmean"], n)],
value = [Mmeans; Fmeans]
)
end
@time result = mfmeans(1000000)
コメント欄で頂いたコードと、黒木さんのJupyter Notebookを参考にしました。
結果こうなりました。
多少ばらつきがありますが、概ね20秒前後です。やっぱりJuliaの方が数倍程度は早いようです。くやしみ。
まとめ
- Rでは乱数生成に結構時間がかかっていました。
- 乱数生成部分を
dqrngパッケージで高速化すると数十秒で計算が終わりました。 -
今回の処理はJuliaだとRの倍かかるという若干怪しい結果が出ました。- 詳しい方々の意見を参考に書き直したらJuliaのが3倍くらい早くなりました。
- 少なくとも「Rでも数十秒で終わる」ことは言えそうです。