はじめに
皆さん、はじめまして！
今回はp5jsを用いて、カルマンフィルタを実装してみようと思います。
私自身、特にプログラミングに詳しいわけではないので、対象は以下となります
対象
- プログラミングに興味がある人
- 環境構築の時点で、やる気ゲージが0になってしまう人
- せっかくプログラミングをするなら、ビジュアルにもこだわりたい人
p5jsとは
p5jsの公式サイトには、次のような説明がされています。
p5jsとは、クリエイティブなコーディングのためのJavaScriptライブラリであり、アーティスト、デザイナー、教育者、初心者など誰にとってもコーディングにアクセスしやすく、受け入れやすいものにすることに重点を置いています。
(公式サイト原文翻訳)
元々、processingというアーティスティックな表現を容易に可能な言語があり、p5jsでは、ブラウザ上で気軽に試すことが可能です。
環境構築しないので、やる気ゲージが失われる前に、取り組めますね！
processingで著名な方に、Daniel Shiffmanという方がおられます。
彼は、processingの開発のリードであり、ニューヨーク大学Tisch School of the Artsスクールの准教授でもあるそうです。
Daniel Shiffmanさんは、Coding TrainというYoutubeチャンネルでprocessingやp5jsを用いて、実際に実装しながらプログラミングの解説をしています。彼のコーディングスタイルは、丁寧かつ陽気なので楽しみながら、プログラミング(と英語)を学ぶことができます。
スネークゲーム
アスキーアート
サムネイルから楽しそうな様子が伝わってきます。陽気ですね。
彼の書籍である「Nature of Code」は、無料で公開されており、またCoding Trainチャンネルのコミュニティもあるので、興味のある方は是非覗いてみてはいかがでしょうか？
カルマンフィルターとは
Daniel Shiffmanさんの宣伝ばかりしていますが、ここからは、カルマンフィルターをp5js上で実装していこうと思います。
カルマンフィルターざっくり説明
カルマンフィルタとは、観測データによって、対象とする物体や現象の真の状態を推定するアルゴリズム(方法論？)です。
アルゴリズムの導出は、(私が説明するのが)難しいので他サイトに任せます。
めちゃざっくり流れだけ説明すると、状態変数というものを定義し、時間発展方程式による予測と観測データによる修正(フィルタ)を繰り返し、状態変数を真の状態に近づけていきます。(と理解しています。)
カルマンフィルタは、目的に応じて、アンサンブルカルマンフィルタ、粒子フィルタなど派生、進歩しており、その活用分野は自動運転システム、天気予報、宇宙ロケットなど、多岐に渡ります。
なんだかカルマンフィルタがかっこよく見えてきました！
今回、カルマンフィルターで表現するもの
今回は、マウスポインタの位置を追跡する点、つまりマウストラッキングを実装してみましょう。位置や速度を推定するのは、自動運転やロケットの姿勢制御にも使われているので、マウストラッキングはその第一歩という感じでワクワクしますね！
数式
書籍やWebサイトを参考に、自分なりに立式してみました。
ここで、自分で考えたのは、状態変数、観測データの定義とそれらを紐づける観測演算子、状態の時間発展方程式です。
それ以外は、カルマンフィルタのアルゴリズムに基づく式になります。
今回は、マウス位置を推定したいのにも関わらず、マウス位置を観測データとしているので、とても簡単な状態推定ができるでしょう。(いわば、真の状態が観測値として得られている状態)
また状態変数に加速度まで追加しましたが、位置、速度だけでもマウス位置の推定は可能です。
本来のカルマンフィルタでは、状態変数の次元が莫大であったり、状態の時間発展が非線形である事象を対象としているために、様々な工夫が施されています。
一例に、スーパーコンピューター富岳を用いて、局所アンサンブル変換カルマンフィルタにより、より高精度に天気予報を行った記事を紹介します。
(大分端折っているので,ぜひリンク先をご覧ください！)
実装
立式した数式をコードにしていきます。
ここでは、すべてのコードについてコメントできないので抜粋して説明します。
文法やライブラリに関しては、公式リファレンスを参照ください
実装ポイント
プログラムの流れ
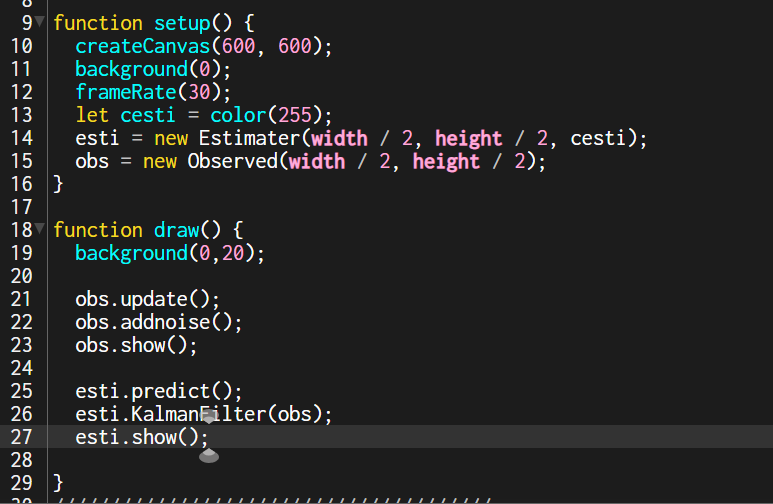
プログラムは、スクリーンショットのように、setup関数とdraw関数で構成されます。
setup関数は、プログラム実行時に1度だけ実行、draw関数は、フレーム毎に実行されます。
ここでは、観測データ(マウス位置)についての処理をObservedクラス、状態変数(推定点)についての処理をEstimaterクラスで定義しています。
それぞれ、毎フレーム(draw関数内)で、以下の処理を行います。
- Observed
- update : マウス位置を更新
- addnoise : 観測データにノイズを加える
- show : マウス位置を描画
- Estimater
- predict : 推定点の現在位置、速度、加速度から次フレームの位置を予測
- KalmanFilter : 観測データ(マウス位置)により、位置を修正
- show : 推定点の描画
マウス位置と推定点の表現
マウス位置は、このようにクロスマークを描画する関数を定義し、位置を引数にし、毎フレーム描画することで、表現しています。
推定点は、シンプルに白点として表現しています。
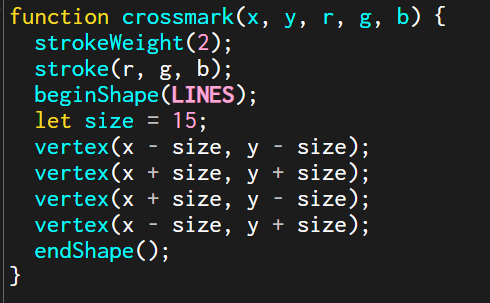
また移動経路が分かりやすいように、残像を見えるようにしています。
実装コードの公開
実装したコードのほとんどにコメントできていないので、こちらで実際のコードと動くものを公開します。
左上のアイコンからコードが参照でき、プログラムを変えて再実行できます。いろいろいじってみてください！
ピンク色のクロスマークがマウスの位置で、白い点が少し遅れながらついてくると思います。
かわいいですね！
実験
カルマンフィルタの特徴を知り、理解を深めるために簡単な実験をしてみましょう。
実験1 : 観測演算子を変更
実験1では、観測データとの紐づき方を変えてみます。
上記のカルマンフィルタでは、観測データと状態変数を紐づける観測演算子Hを以下のように定義してみました。1,0をうまく配置し、定義することで、観測データと状態変数の位置を紐づけています。
H = \begin{bmatrix}1 & 0 & 0 & 0 & 0& 0\\0 & 1 & 0 & 0 & 0& 0 \end{bmatrix}
こちらを、下記のように変更してみます。2列2行目の1が0になりました。観測データと推定点の位置のx座標のみしか紐づけられていないことを意味します。
H = \begin{bmatrix}1 & 0 & 0 & 0 & 0& 0\\0 & 0 & 0 & 0 & 0& 0 \end{bmatrix}
この状態で、マウストラッキングを行うとどうなるでしょうか？
以下のリンクから体験できます。
スクリーンショットから分かる通り、x方向には追従しているものの、マウス位置のy座標が観測データとして渡されていないので、y方向には追従されていないです。
実際のカルマンフィルタでは、観測データが何かを把握し、そこから現実的に推定できる状態変数を整理し、観測演算子を定義すべきでしょう。
実験2 : フィルタ頻度を変更
実験2では、フィルタリングを行う頻度を変えてみます。先ほどまでは、予測とフィルタを交互に行っていました。しかし、現実の事象では、予測の時間増分と観測データの得られる頻度が同等であるとは限りません。ここでは、10回の予測をした後、1回の観測データが得られるとします。
実験2のコードがこちらです。
スクリーンショットでは、少し分かりにくいですが、マウスがカーブしていても、その時点で観測データが渡されていないので、推定点はまっすぐ進んでいます。そして、10回予測した後、最新の観測データにより、位置が修正されています。マウスを早く動かせば動かすほど、推定点はその時点の加速度から次点のマウス位置を予想し、遠くに飛んでいきます。
最後に
この記事では、気軽にプログラミングができるp5jsの紹介、様々な分野で活用されているカルマンフィルタの紹介と実装、数式やコードをいじる実験をしてみました。
初投稿記事ということもあり、不十分な点が多くあると思いますが、これを機にp5js等でのプログラミングをはじめてみたり、カルマンフィルタに興味を持っていただけたりすると嬉しいです。
不明点、間違っている点あれば、コメントお願いします！
ここまでお読みいただきありがとうございました！🎉