LoginSignup
8
4
@nouka28

一次方程式をUnionFindに乗せる　〜dsu_equationを作ろう〜

Posted at

この記事は 競プロ Advent Calendar 2023 の19日目の記事として書かれました。

0. はじめに

など重み付きUnionFindを貼るだけで解ける問題は少なくありません。
この記事ではさらにUnionFindに一次方程式を乗せることでより多くのバリエーションの問題に対応できるデータ構造の作成を目指していきます。

前提知識

UnionFindに関しては既知とします。重み付きUnionFindから順に紹介するので重み付きUnionFindは知らなくても大丈夫です。
なお重み付きUnionFindについてはけんちょんさんの素晴らしい記事があります。
https://qiita.com/drken/items/cce6fc5c579051e64fab

ここでも重み付きUnionFindについて説明しますが、こちらを見ても構いません。

1. 重み付きUnionFindについて

※知っている方は読み飛ばしても構いません。

重み付きUnionFindは以下のような問題を高速に解きます。

長さ $N$ の数列 $A$ があり、$Q$ 個のクエリが与えられます。

  • $1$ $x$ $y$ $d$ : $A[x]-A[y]=d$　が成り立っています。
  • $2$ $x$ $y$     : $A[x]-A[y]$ が定まる場合はその値、それ以外は"AMBIGUOUS"と出力しなさい。

重み付きUnionFindは以下の処理をサポートします。

クエリ 内容
merge( x, y, d ) $A[x] - A[y] = d$ として $x$ , $y$ をマージ
same( x, y ) $x$ , $y$ が同じグループに含まれるか
diff( x, y ) $A[x] - A[y]$ が一意に定まる場合はその値を求める

考え方は普通のUnionFindと同じです。
木のような構造で管理して、各ノードでは親と親との差分を管理します。

weighted_union_find.png

各ノードの親 ( par ) と親との差分( diff_weight )

0 1 2 3 4
par -1 0 0 1 1
diff_weight 3 2 -5 -1

1-1. merge( x , y , d ) の処理

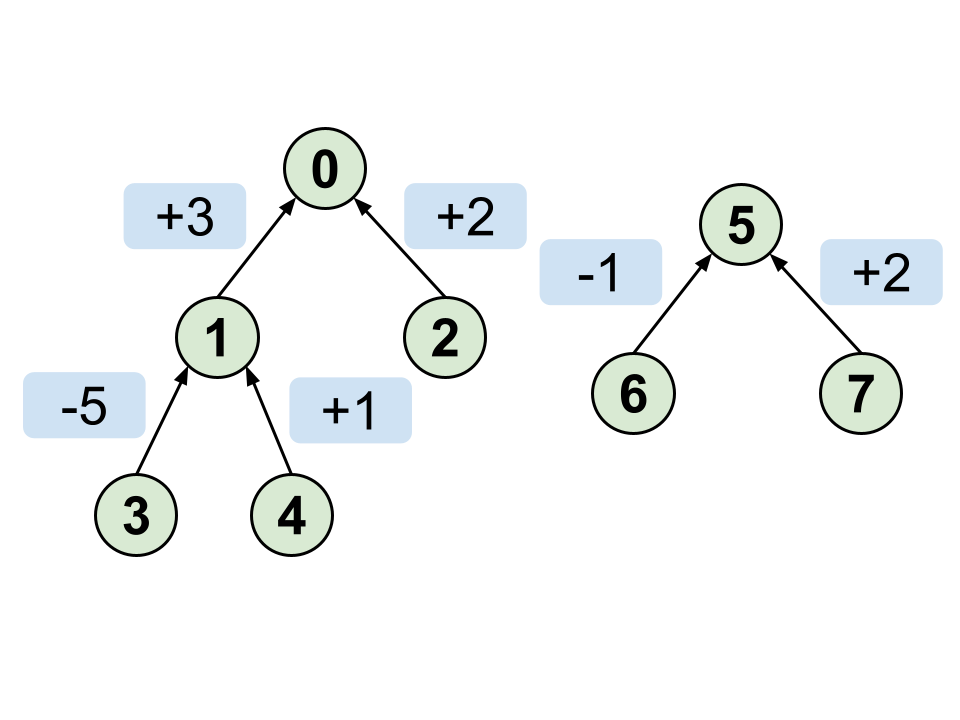
weighted_union_find_merge1.png

merge( x , y , d ) の処理を上の2つの木で考えてみます。
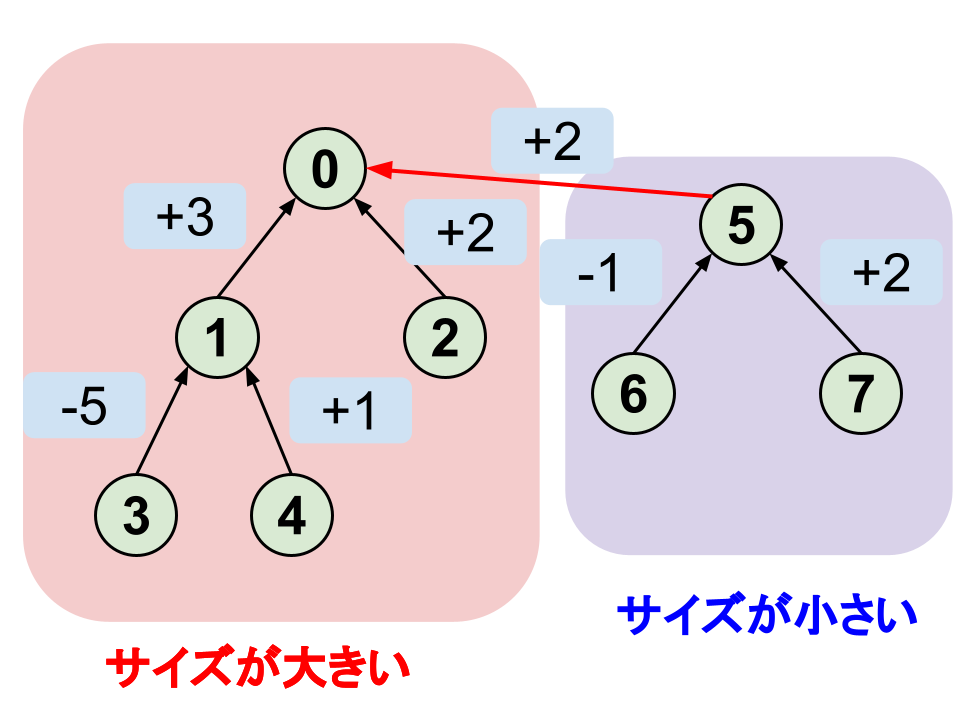
例えば $1$ $3$ $6$ $5$ というクエリ、つまり $A[3] - A[6] = 5$ であるという情報が与えられたとします。

普通のUnionFindで同じグループにあるのかをその木の代表点で表したように
重み付きUnionFindでは代表点との差分を計算してグループ（木）のマージをします。

つまり 3 が含まれている木の代表点は 0 なので
3から親に向かってたどっていくことで $A[0] = A[3] + (- 5 + 3 ) = A[3] - 2$

同じように 6 が含まれている木の代表点は 5 なので
6から親に向かってたどっていくことで $A[5] = A[6] - 1 $

これを $A[3] - A[6] = 5$　に代入して $( A[0] + 2 ) - ( A[5] + 1 ) = 5$
つまり $A[0] - A[5] = 2$ と2つの代表点の差分に言い換えることができます。

よって $A[0] = A[5] + 2$ から $A[5]$ から $A[0]$ に重み2の辺を張ればいいことがわかります。（下図）

weighted_union_find_merge2.png

より一般的にいうと、

$x$ , $y$ の代表点を $rootx$ , $rooty$ とすると $A[x] - A[y] = d$ となるならば
$A[rootx] = A[x] + weight(x)$ , $A[rooty] = A[y] + weight(y)$
※$weight(x)$ は $x$ の 代表点と $x$ との差分
となるので、

$( A[rootx] - weight(x) ) - ( A[rooty] - weight(y) ) = d$
したがって、 $A[rootx] - A[rooty] = d + weight(x) - weight(y)$

と代表点同士の差分に言い換えることができます。

また、マージの仕方によっては下図のようにとても深い木ができてしまう可能性があります。

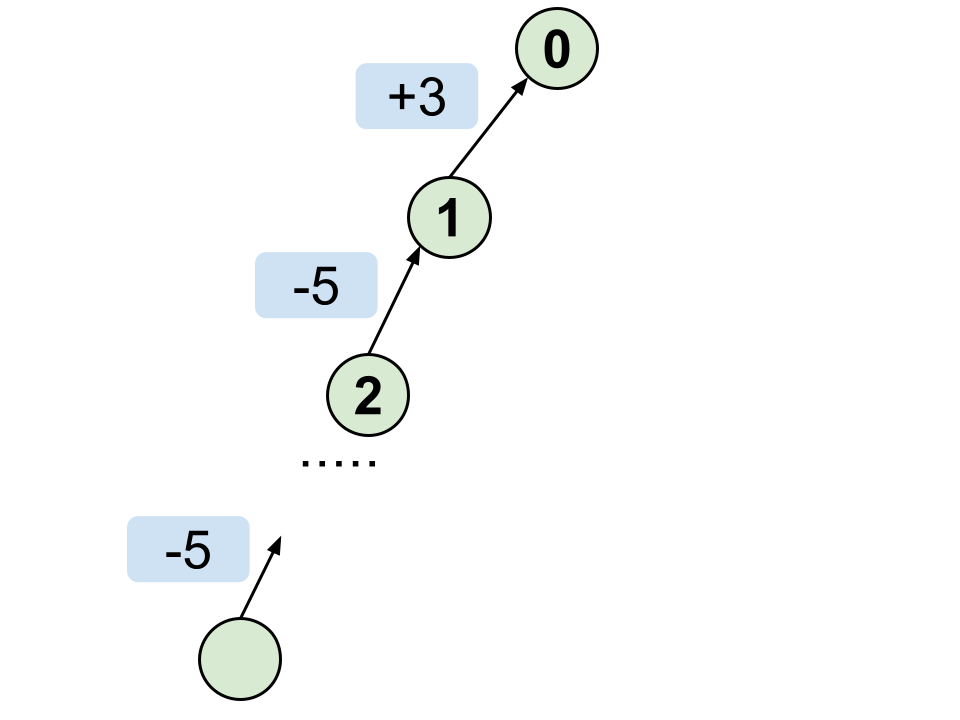
weighted_union_find_merge4 (1).png

このような木では木の葉から代表点に向かう処理が $O(N)$ となってしまう可能性があり、実行時間に間に合わなくなります。
これを避けるためにマージするときに木の高さはなるべく低くする必要があります。
いくつかの方法がありますが、
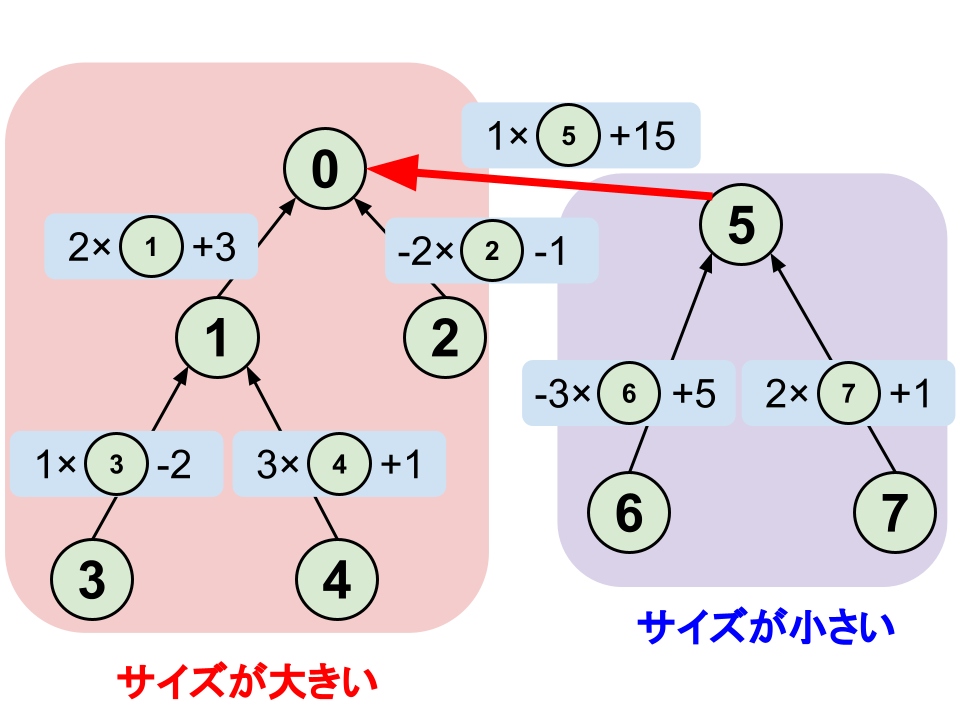
今回はサイズの小さい木から大きい木に向けて辺をはるという方法で実装します。

weighted_union_find_merge3.png

このようにすると木の高さが $O(logN)$ になるため、
木の葉から代表点に向かう処理も $O(logN)$ となり、十分高速に行われていることがわかります。

1-2. diff( x , y ) の処理

weighted_union_find_merge3 (1).png

次はこの木で diff( x , y ) の処理について考えてみます。

例えば $2$ $4$ $7$ つまり $A[4] - A[7]$ を求めなさいというクエリが与えられたとします。

diff( x , y ) でも merge と同じように代表点との差分の問題に言い換えます。

$A[4] - A[7] = (A[0] - A[7]) - (A[0] - A[4])$ となるので

$A[0] - A[7] = 2 + 2 = 4 , A[0] - A[4] = 1 + 3 = 4$
から $A[4] - A[7] = 4 - 4 = 0$ という感じで求めます。

一般に $A[x] - A[y]$ を計算しなさいというクエリが与えれたら、
$x$ , $y$ の代表点を $root$ として $( A[root] - A[y] ) - (A[root] - A[x] )$
つまり $weight(y) - weight(x)$ を求めればいいことがわかります。

計算量はある頂点からその代表点までの距離、つまり木の高さとなるので $O(logN)$ となることがわかります。

1-3. 実装

以下に実装を示します。
なおここで $e$ は単位元です。つまり $x + e = x$ を満たす $e$ のことです。整数なら $0$ です。

template<typename T>
class weighted_union_find{
    vector<int> par;
    vector<int> siz;
    vector<T> df;
    T e;
public:
    weighted_union_find(int n=1,T e_=0){
        init(n,e_);
    }
    void init(int n=1,T e_=0){
        e=e_;
        par.resize(n,-1);
        siz.resize(n,1);
        df.resize(n,e);
    }
    int leader(int x){
        while(par[x]!=-1){
            x=par[x];
        }
        return x;
    }
    T weight(int x){
        T res=e;
        while(par[x]!=-1){
            res+=df[x];
            x=par[x];
        }
        return res;
    }
    int size(int x){
        return siz[leader(x)];
    }
    int same(int x,int y){
        return leader(x)==leader(y);
    }
    bool merge(int x,int y,T d){
        d+=weight(x);d-=weight(y);
        x=leader(x),y=leader(y);
        if(x==y)return false;
        if(siz[x]<siz[y]){swap(x,y);d=-d;}
        siz[x]=siz[x]+siz[y];
        par[y]=x;
        df[y]=d;
        return true;
    }
    T diff(int x,int y){
        return weight(y)-weight(x);
    }
};

verify : https://atcoder.jp/contests/abc328/submissions/47606387

2.dsu_equation について

いよいよ本題です。1次方程式を扱うUnionFindについて自分で調べたところ
それっぽいサイトがなかったので（あったら教えてください）ここでは1次方程式を扱うUnionFindをdsu_equation (disjoint set union _equation)の略。と呼ぶことにします。

dsu_equation は以下のような問題を高速に解きます

  • 1 $x$ $y$ $a$ $b$ $c$ : $a\cdot A[x]+b\cdot A[y] = c$ が成り立っています
  • 2 $x$ : $A[x]$ が一意に定まるならばその値を、そうでないなら"AMBIGUOUS"と出力しないさい
  • 3 $x$ $y$ : $A[y]=p\cdot A[x]+q$ を満たす$p$,$q$ があればその値を、そうでないなら"AMBIGUOUS"と出力しないさい

dsu_equation は以下の処理をサポートします

クエリ 内容
merge( x , y , a , b , c ) $a\cdot A[x]+b\cdot A[y] = c$ として$x$ , $y$ をマージ
same( x , y ) $x$ , $y$ が同じグループに含まれるか
solve_coef( x , y ) $A[y]=p\cdot A[x]+q$ を満たす$p$,$q$ を求める
specify( x ) $A[x]$　が一意に定まるならその値を求める
set_val( x , f ) $A[x]=f$ として定める

考え方は重み付きUnionFindと同じです。
木のような構造で管理して、各ノードでは親と親との関係を管理します。

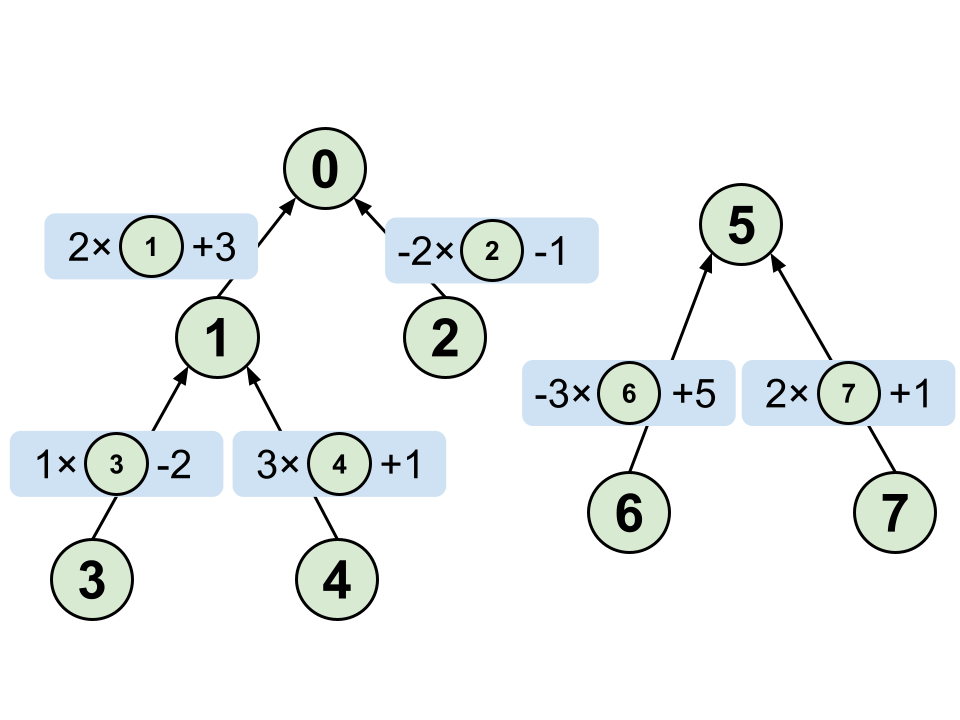
dsu_equation.png
0 1 2 3 4 5 6 7
par -1 0 0 1 1 -1 5 5
coef1 2 -2 1 3 -3 2
coef2 3 -1 -2 1 5 1

2-1. 分数ライブラリを作ろう！!

不定方程式を解くと以下のように分数が出てきてしまいます。

$\displaystyle 2x+3y=5\Rightarrow x=-\frac{3}{2}y+\frac{5}{2}$

これに対応するために分数ライブラリを作ります。

template<class T>
struct Fraction{
    T Bunsi,Bunbo;
    Fraction(T Bunsi=0,T Bunbo=1)noexcept:Bunsi(Bunsi),Bunbo(Bunbo){reduce();}
    void reduce(){
        if(Bunbo<0){Bunbo=-Bunbo;Bunsi=-Bunsi;}
        if(Bunsi==0){Bunbo=1;return;}
        T GCD=gcd(abs(Bunsi),abs(Bunbo));
        Bunsi/=GCD;Bunbo/=GCD;
    }
    const Fraction<T>& operator++(){
        Bunsi+=Bunbo;reduce();return *this;
    }
    const Fraction<T>& operator--(){
        Bunsi-=Bunbo;reduce();return *this;
    }
    const Fraction<T>& operator+=(const Fraction<T>& rhs)noexcept{
        Bunsi=Bunsi*rhs.Bunbo+Bunbo*rhs.Bunsi;
        Bunbo=Bunbo*rhs.Bunbo;reduce();
        return *this;
    }
    const Fraction<T>& operator-=(const Fraction<T>& rhs)noexcept{
        Bunsi=Bunsi*rhs.Bunbo-Bunbo*rhs.Bunsi;
        Bunbo=Bunbo*rhs.Bunbo;reduce();
        return *this;
    }
    const Fraction<T>& operator*=(const Fraction<T>& rhs)noexcept{
        Bunsi=Bunsi*rhs.Bunsi;
        Bunbo=Bunbo*rhs.Bunbo;reduce();
        return *this;
    }
    const Fraction<T>& operator/=(const Fraction<T>& rhs)noexcept{
        Bunsi*=rhs.Bunbo;
        Bunbo*=rhs.Bunsi;reduce();
        return *this;
    }

    friend Fraction<T> operator+(const Fraction<T> &lhs,const Fraction<T> &rhs)noexcept{
        return Fraction(lhs)+=rhs;
    }
    friend Fraction<T> operator-(const Fraction<T> &lhs,const Fraction<T> &rhs)noexcept{
        return Fraction(lhs)-=rhs;
    }
    friend Fraction<T> operator*(const Fraction<T> &lhs,const Fraction<T> &rhs)noexcept{
        return Fraction(lhs)*=rhs;
    }
    friend Fraction<T> operator/(const Fraction<T> &lhs,const Fraction<T> &rhs)noexcept{
        return Fraction(lhs)/=rhs;
    }
    constexpr bool operator<(const Fraction<T> &rhs)const noexcept{
        return Bunsi*rhs.Bunbo<Bunbo*rhs.Bunsi;
    }
    constexpr bool operator<=(const Fraction<T> &rhs)const noexcept{
        return Bunsi*rhs.Bunbo<=Bunbo*rhs.Bunsi;
    }
    constexpr bool operator>(const Fraction<T> &rhs)const noexcept{
        return Bunsi*rhs.Bunbo>Bunbo*rhs.Bunsi;
    }
    constexpr bool operator>=(const Fraction<T> &rhs)const noexcept{
        return Bunsi*rhs.Bunbo>=Bunbo*rhs.Bunsi;
    }
    constexpr bool operator==(const Fraction<T> &rhs)const noexcept{
        return Bunsi*rhs.Bunbo==Bunbo*rhs.Bunsi;
    }
    constexpr bool operator!=(const Fraction<T> &rhs)const noexcept{
        return Bunsi*rhs.Bunbo!=Bunbo*rhs.Bunsi;
    }
    
};

2-2. merge(x , y , a , b , c)の処理　(x,yが違うグループのとき）

dsu_equation.png

merge(x , y , a , b , c)　の処理を上の2つの木で考えてみます。
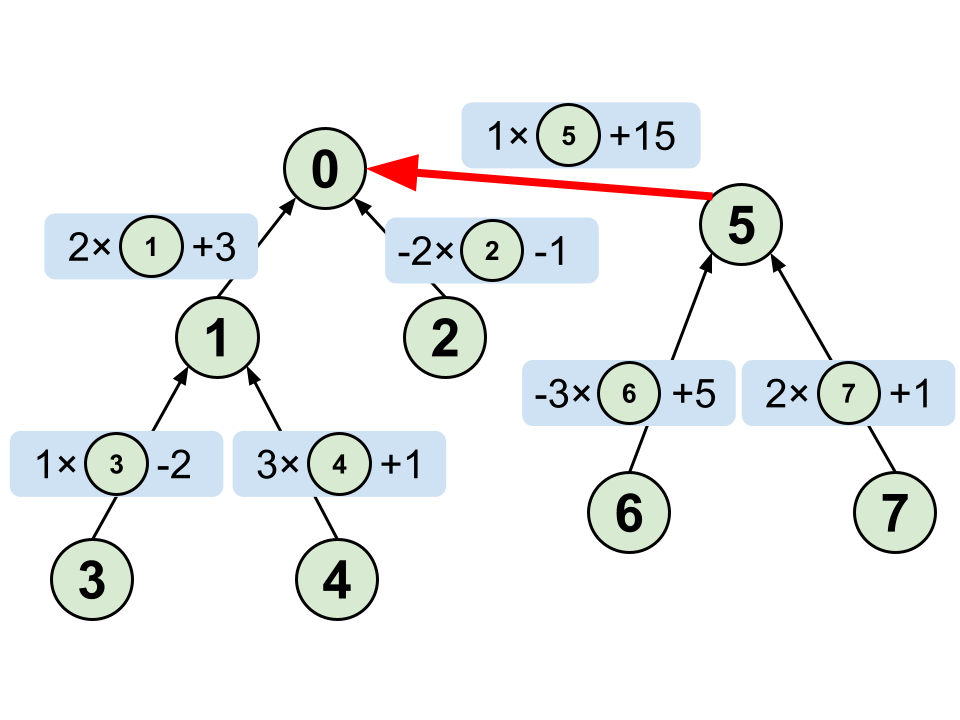
例えば $1$ $1$ $6$ $2$ $3$ $7$ というクエリ、つまり $2\cdot A[1]+3\cdot A[6]=7$ という情報が与えられたとします。

重みつきUnionFindと同じで代表点に関する式にします。

1 が含まれている木の代表点は 0 なので
1から親に向かってたどっていくことで $A[0]=2\cdot A[1]+3$

6 が含まれている木の代表点は 5 なので
6から親に向かってたどっていくことで $A[5]=-3\cdot A[6]+5$

したがって $\displaystyle A[1]=\frac{1}{2}A[0]-\frac{3}{2}$ , $\displaystyle A[6]=-\frac{1}{3}A[5]-\frac{5}{3}$

$\displaystyle 2\cdot A[1]+3\cdot A[6]=7 \Rightarrow 2\cdot \left(\frac{1}{2}A[0]-\frac{3}{2}\right)+3\cdot \left(-\frac{1}{3}A[5]-\frac{5}{3}\right)=7$

整理して、 $\displaystyle A[0]-A[5]=15\Rightarrow A[0]=A[5]+15$ より以下のように辺を張ります。

dsu_equation

一般に $a\cdot A[x]+b\cdot A[y] =c$ という情報が与えられたときに

$x,y$ の代表点をそれぞれ $rootx,rooty$ として、$x,y$ から代表点までたどっていくことによって
$A[rootx]=p_x\cdot A[x]+q_x , A[rooty]=p_y\cdot A[y]+q_y$ と表せたとすると

$\displaystyle A[x]=\frac{1}{p_x}A[rootx]-\frac{q_x}{p_x}$ , $\displaystyle A[y]=\frac{1}{p_y}A[rooty]-\frac{q_y}{p_y}$ から

$\displaystyle a\cdot \left(\frac{1}{p_x}A[rootx]-\frac{q_x}{p_x}\right)+b\cdot \left(\frac{1}{p_y}A[rooty]-\frac{q_y}{p_y}\right) =c$

$\displaystyle \frac{a}{p_x}A[rootx]+\frac{b}{p_y}A[rooty]=\frac{aq_x}{p_x}+\frac{bq_y}{p_y}+c$

$\displaystyle A[rootx]=-\frac{bp_x}{ap_y}A[rooty]+\left(q_x+\frac{bp_xq_y}{ap_y}+\frac{cp_x}{a}\right)$

このようにマージすることができます。

dsu_equation

これも同じようにサイズの小さい木から大きい木に向けて辺をはるという方法で実装します。

2-3. merge(x , y , a , b , c)の処理　(x,yが同じグループのとき）

$x,y$ のグループが同じときに $A[x],A[y]$ の値が一意に定まる可能性があります。

$x,y$ の代表点を $root$ として、$A[root]=p_x\cdot A[x]+q_x$ , $A[root]=p_y\cdot A[y]+q_y$ と表せたとき

$\displaystyle A[x]=\frac{1}{p_x}A[root]-\frac{q_x}{p_x}$ , $\displaystyle A[y]=\frac{1}{p_y}A[root]-\frac{q_y}{p_y}$

$\displaystyle a\cdot A[x]+b\cdot A[y]=c \Rightarrow a\left(\frac{1}{p_x}A[root]-\frac{q_x}{p_x}\right)+b\left(\frac{1}{p_y}A[root]-\frac{q_y}{p_y}\right)=c$ から

$\displaystyle \left(\frac{a}{p_x}+\frac{b}{p_y}\right)A[root]=\frac{aq_x}{p_x}+\frac{bq_y}{p_y}+c$ , $\displaystyle A[root]=\frac{ap_yq_x+bp_xq_y+cp_xp_y}{ap_y+bp_x}$

$A[root]$ の分母の $ap_y+bp_x$ が $0$ でないならば $A[root]$ の値が一意に定ります。

（ $ap_y+bp_x=0$ の時、$\displaystyle -\frac{aq_x}{p_x}-\frac{bq_y}{p_y}\neq c$ であれば矛盾していることがわかります。　）

グループの一点が一意に定まればそのグループの他の点も一意に定まるので、代表点に一意に定まるならばその値を格納しておきます。

2-4 solve_coef の処理

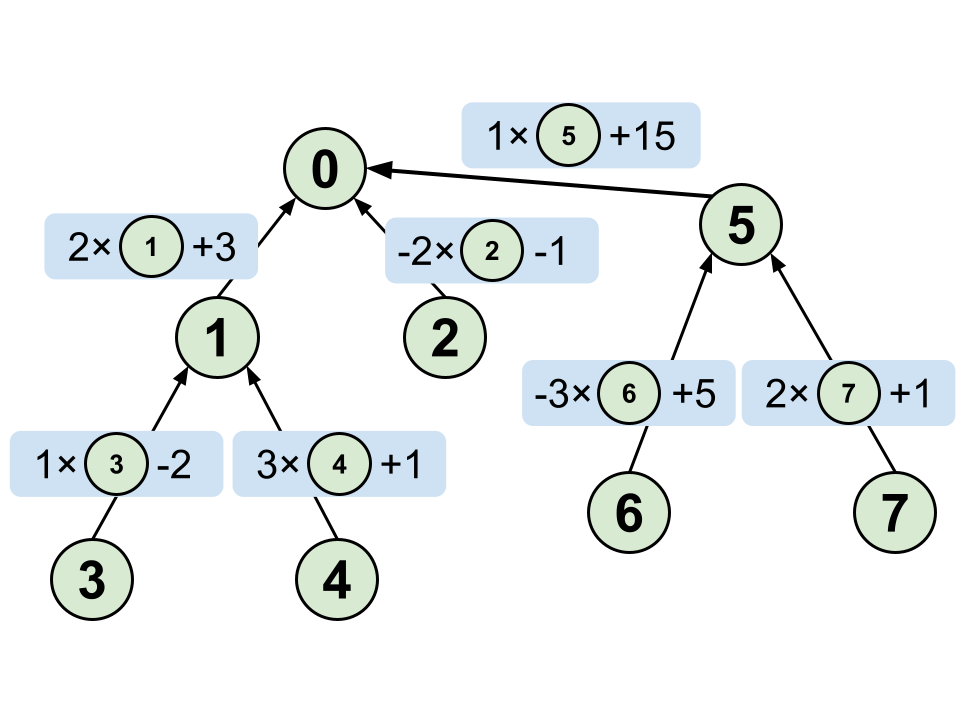
dsu_equation

上の木を使って考えてみましょう。
例えば solve_coef(4,6) というクエリが与えられたとします。

4 から 0 にたどっていくことで

$A[1]=3\cdot A[4]+1$ , $A[0]=2\cdot A[1]+3=2\cdot(3\cdot A[4]+1)+3=6\cdot A[4]+5$

6 から 0 にたどっていくことで

$A[6]=-3\cdot A[5]+5$ , $A[0]=A[5]+15=-3\cdot A[6]+20$

と $A[4]$ , $A[6]$ を $A[0]$ についての式で表せることができました

よって $6\cdot A[4]+5=-3\cdot A[6]+20$

$\displaystyle A[6]=-\frac{1}{3}A[4]+5$ と $A[6]$ について解いてあげることができます。

一般に

$x,y$ が含まれるグループの代表点を $root$ とする

$x,y$ からそれぞれ $root$ まで辿っていくことで

$A[root]=p_x\cdot A[x]+q_x$

$A[root]=p_y\cdot A[y]+q_y$

を満たす $p_x,q_x,p_y,q_y$ が求められる

$p_x\cdot A[x]+q_x=p_y\cdot A[y]+q_y$

$\displaystyle A[y]=\frac{p_x}{p_y}A[x]+\frac{q_x-q_y}{p_y}$

と表すことができるとわかります。

2-5. 実装

以下を踏まえて実装すると以下のようになります。

struct dsu_equation{
    using frac=Fraction<ll>;
private:
    vector<int> par; //parent
    vector<int> siz; //size
    vector<frac> coef_p,coef_q; //coefficient
    vector<bool> specify_; //is value uniquely determined
    vector<frac> val; //value
public:
    dsu_equation(int n=0){
        par.resize(n);
        siz.resize(n);
        coef_p.resize(n);
        coef_q.resize(n);
        specify_.resize(n);
        val.resize(n);
        for(int i=0;i<n;i++){
            par[i]=i;
            siz[i]=1;
        }
    }

    //Find a leader of the group contains x
    int leader(int x){
        if(par[x]==x)return x;
        return leader(par[x]);
    }

    //Find the size of the group contains x
    int size(int x){
        return siz[leader(x)];
    }

    //Check if x y are in the same group
    bool same(int x,int y){
        return leader(x)==leader(y);
    }
    
    //return rootx(leader of x) , p , q satisfying A[rootx] = p * A[x] + q 
    tuple<int,frac,frac> relationship(int x,frac p=1,frac q=0){
        if(par[x]==x)return {x,p,q};
        return relationship(par[x],p*coef_p[x],q*coef_p[x]+coef_q[x]);
    }

    //unite as a * A[x] + b * A[y] = c
    //return false if contradiction else true
    //must satisfy a != 0 and b != 0
    bool merge(int x,int y,int a,int b,int c){
        assert(a!=0&&b!=0);
        auto [rx,px,qx]=relationship(x);
        auto [ry,py,qy]=relationship(y);
        if(specify_[rx]&&specify_[ry]){
            return (a*(val[rx]/px-qx/px)+b*(val[ry]/py-qy/py)==c);
        }
        if(rx==ry){
            //value is determined uniquely or other
            frac ca=a/px+b/py,cb=c+a*qx/px+b*qy/py;
            if(ca==0)return cb==0;
            specify_[rx]=true;
            val[rx]=cb/ca;
            return true;
        }else{
            if(siz[rx]<siz[ry]){
                swap(rx,ry),swap(a,b),swap(px,py),swap(qx,qy);
            }
            par[ry]=rx;
            siz[rx]+=siz[ry];
            coef_p[ry]=(-b*px)/(a*py);
            coef_q[ry]=(qx+b*px*qy/(a*py)+(c*px)/a);
            if(specify_[ry]){
                val[rx]=coef_p[ry]*val[ry]+coef_q[ry];
            }
            return true;
        }
    }

    //set as A[x]=f , return false if contradiction else true
    bool set_val(int x,frac f){
        auto [rx,px,qx]=relationship(x);
        if(specify_[rx])return px*f+qx==val[rx];
        else {val[rx]=px*f+qx;return specify_[rx]=true;}
    }
    
    //return {is A[x] uniquely determined ?, its value}
    pair<bool,frac> specify(int x){
        auto [rx,px,qx]=relationship(x);
        if(!specify_[rx])return {false,0};
        return {true,val[rx]/px-qx/px};
    }

    //return {p,q} satisfying A[y] = p * A[x] + q 
    tuple<bool,frac,frac> solve_coef(int x,int y){
        auto [rx,px,qx]=relationship(x);
        auto [ry,py,qy]=relationship(y);
        if(rx!=ry)return {false,0,0};
        return {true,px/py,(qx-qy)/py};
    }
};

説明：

関数名 機能 計算量
dsu_equation(int N) 長さ $N$ の数列 $A$ として初期化。 $O(N)$
int leader(int x) $x$ が含まれるグループのリーダーを返す $O(\log N)$
int size(int x) $x$ が含まれているグループのサイズを返す。 $O(\log N)$
bool same(int x,int y) $x,y$ が含まれているグループが同じかどうかを返す。 $O(\log N)$
tuple<int,frac,frac> relationship(int x,int p=1,int q=0) $x$ 含まれているグループのリーダーを $root_x$ としたときに $A[root_x]=p\cdot A[x]+q$ と表せられる $p,q$ を求め $root_x,p,q$ を返す。 $O(\log N)$
bool merge(int x,int y,int a,int b,int c) $a\cdot A[x]+b\cdot A[y]=c$ として $x,y$ をマージ 矛盾しないなら true , しているなら false を返す。 $O(\log N)$
bool set_val(int x,frac f) $A[x] = f$ としてセット これまでの情報に矛盾しないならtrue , しているなら false を返す。 $O(\log N)$
pair<bool,frac> specify(int x) $A[x]$ の値を求める。一意に定まらないなら {false,0} を返す。そうでないなら {true,A[x]} を返す。 $O(\log N)$
tuple<bool,frac,frac> solve_coef(int x,int y) $A[y]=p\cdot A[x]+q$ を満たす $(p,q)$ を返す。一意に定まらないなら {false,0,0} を返す。そうでないなら {true,p,q} を返す。 $O(\log N)$

2-6.使用例

1 . ABC328 F - Good Set Query

dsu_equation::merge は矛盾していれば false , そうでないなら true を返してくれます。
よってこれだけで解けます。

#include<bits/stdc++.h>
using namespace std;
using ll=long long;

int main(){
    int N,Q;
    cin>>N>>Q;
    dsu_equation ds(N);
    for(int i=0;i<Q;i++){
        int a,b,d;
        cin>>a>>b>>d;a--;b--;
        if(ds.merge(a,b,1,-1,d))cout<<i+1<<"\n";
    }
}

2. 068 - Paired Information

クエリタイプ1については
$A[Y_i]=p\cdot A[X_i]+q$ を満たす $p,q$ を求めて $A[X_i]$ に $V_i$ を代入すればいいことがわかります。

#include<bits/stdc++.h>
using namespace std;
using ll=long long;

int n,q;
int main(){
    cin>>n>>q;
    dsu_equation ds(n);
    for(int i=0;i<q;i++){
        int t,x,y,v;
        cin>>t>>x>>y>>v;
        if(t==0){
            x--;y--;
            ds.merge(x,y,1,1,v);
        }else{
            x--;y--;
            auto [f,p,q]=ds.solve_coef(x,y);
            if(!f)cout<<"Ambiguous"<<endl;
            else cout<<(p*v+q).Bunsi<<endl;
        }
    }
}

3.終わりに

掛け算を扱っている時点でmergeの時に$|a|>1$ , $|b|>1$ がたくさん与えられてしまうと方程式を解く時に係数がとても大きくなってしまいオーバーフローしてしまう可能性があります。
しかし Weighted Union Find　の上位互換ではあると思うので許してください。

最後まで読んでいただいてありがとうございました。
みなさんも、良い dsu_equation ライフを！

8
4
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
8
4