はじめに
量子計算には、 離散量 と 連続量 という二種類があります。
離散量を扱う目的では超伝導、イオントラップなどの実装が知られています。
離散量の場合、1量子は$0$か$1$か(あるいはその重ね合わせ)を取ります。状態は2つの複素数$\alpha,\beta$で指定できます。
量子の単位は 量子ビット と呼ばれ、イオン2個なら2量子ビットです。
連続量を扱う目的では光量子などの実装が知られています。
連続量の場合、1量子の状態は無数の複素数で指定されます。
例えば光量子の”位置$x$”を基底と考えると $\int_{x=-\inf}^{x=+\inf} x_{coeff.}|x> dx$ のような形で書けます。イメージとして。
同じように運動量$p$は $\int_{p=-\inf}^{p=+\inf} p_{coeff.}|p> dp$となります。
また、$x,p$の他に光子の個数$n$に着目した表現方法もあり、
$\sum_{n=0}^{n=+\inf} n_{coeff.}|n>$
このようになります。
基本としては ${x,p}$表現 or ${n}表現$ を使います。
両者は(多くの場合は)基底のとり方が違うだけなので、互いに行き来が可能です。
量子の単位は 量子モード と呼ばれます。光量子の場合、例えば飛行経路が明らかに違う光子2つは別物とみなせるので、2量子モードといいます。
それぞれの量子モードに対して「光子数」という概念がありますから、その合成系は
$\sum_{n=0}^{n=+\inf}\sum_{m=0}^{m=+\inf} n_{coeff.}|n> \otimes m_{coeff.}|m>$
このようになることに注意します。
連続量のほうが連続濃度だから何でもできそうじゃん! と思うわけですが、
どんな値でも取りうるということは、所望の結果なのか所望でない結果だけども雑音で誤ってしまってそうなったのかが区別できないことを意味します。
つまり誤り訂正が出来ません。
誤り訂正をするには何らか「離散化」をせざるを得ません。
そうはいっても連続濃度でなにか遊ぼうということで機械学習とのコラボなど考えられています。
今回は連続量量子で機械学習してみます。
関数近似してみる
このdemoを使います。
データは自分で生成します。
X = np.linspace(-1,1,50,requires_grad=False)
Y = np.sin(np.pi*X,requires_grad=False)
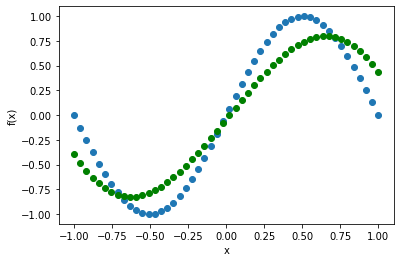
demo通りやってみますが、計算が遅いので途中で学習を打ち切ります。。
目標(青色)になろうとしている量子回路出力(緑色)が見えますね。
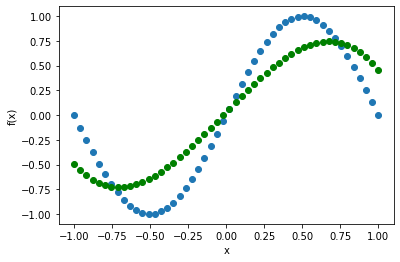
層数を半分にしてみます。
あまり変わりません。
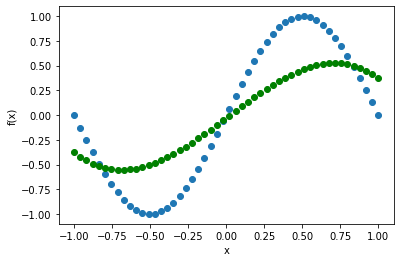
1層にまでしてみます。
さすがに精度が悪くなりました。
これだけみると、「ニューラルネットワークと同じ感じで使えそうじゃん」と思うわけですが・・・
落とし穴:入力データのスケールへの依存性
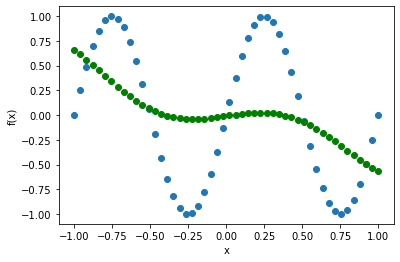
x -> 2x と置き換えたデータ(xを2倍)を近似させてみます。
すると・・・
全くできなくなります。
ちなみに離散量でもこれと似た現象が起きます。
言い過ぎになるかもしれませんが、そもそもsin(x)という目標自体が「この量子回路でうまく近似できるように恣意的に選ばれた例」だと思っています。
スケールすらも、もとからうまくいくように合わせこまれているのです。
sin(x)ができるから他の関数も当然できる と誤解しかねませんので、イマイチ不親切かと思います。
「層数増やしたりすれば任意関数でうまくいくんじゃないの?」と思われるかもしれませんが、実際やってみるとそれも難しいです。モデルを大きくすると、パラメータ最適化がうまくできなくなることが知られているためです。
確かにパラメータ調整(機械学習)により量子回路出力をある程度加工することは出来ますが、量子回路固有の性質(例えばデータを位相角に埋め込んだ場合は必ず$2\pi$周期性が出る)を消し去ることは出来ません。
ニューラルネットワークの場合は、活性化関数がsigmoidだからといって出力がsigmoidっぽくなってしまうことはあまりなかったかと思いますが、量子の場合はかなり引っ張られます。
なので、むしろ量子の性質が活きるような問題を考える/与えてやるという重要度が高いと思います。
量子を自分の色に染めようとすると、なかなか染まらなくて苦労します。
結論
・連続量で遊ぶのは楽しい
・量子機械学習も、量子の性質が活きるような問題を考える/与えてやることが重要かもしれない。