量子位相推定アルゴリズム(QPE)
量子コンピュータで高速化が可能なアルゴリズム(かつ汎用性が高い)として、量子位相推定(Quantum Phase Estimation : QPE)があります。
今回は、このアルゴリズムを勉強してみます。
教材は以下の通り。
https://dojo.qulacs.org/ja/latest/notebooks/2.4_phase_estimation_beginner.html
QPEで何が出来るか
ユニタリ行列の固有値と固有ベクトルが分かります。
ただし、「ある精度で」
QPEの入出力
$2 \times 2$のユニタリ行列$U$を考えます。
$U$の作用する相手は$2$次元の縦ベクトルですから、$\log_{2}(2)=1$ 個のqubitで表現できます。
また、固有値を書き込む先として $3$個の(補助)qubitを使います。
この"3"という値が、固有値を精度$2^{-3}$で推定しますよ、という意味になっています。
回路全体としては$ 1 + 3$ 個の量子ビットを必要とします。
$U$の固有値を$e^{i\lambda_{1},\lambda_{2}}$,対応する固有ベクトルを$|\psi_{1}\rangle, |\psi_{2}\rangle$ とします。
ここで、ユニタリ行列の固有値は必ず絶対値1であり、$e^{i\theta}$とおけることを用いました。
QPEの入力は、$|\psi_{1}\rangle$か$|\psi_{2}\rangle$のいずれかです。
今回は $|\psi_{1}\rangle$ を入力とします。
また、補助量子ビット$|j_{1} \rangle, |j_{2} \rangle, |j_{3} \rangle$はいずれも$|0\rangle$に初期化します。
QPE実行後、補助量子ビット$|j_{1} \rangle, |j_{2} \rangle, |j_{3} \rangle$を($Z$基底で)測定します。
例えば $j_{1} = 0, j_{2} = 0, j_{3} = 1$ のように得られます。
これが固有値の位相$\lambda_{1}$を$2\pi$で規格化したものになっており、$\lambda_{1}$は簡単に再生できます。
この点は後ほど。
他方、$|\psi_{1}\rangle$のQPE出力は$|\psi_{1}\rangle$のままになっています。
固有値の再生
例えば、QPE出力の測定結果が
$j_{1} = 0, j_{2} = 0, j_{3} = 1$
であったとします。
これは、固有値の位相$\lambda = 2\pi(02^{-1}+02^{-2}+1*2^{-3})$を意味します。
言い換えれば、$j_{1,2,3}$というのは$\lambda /2\pi$ (これは必ず1未満の値)を負の2進数で表示したものになっています。
ともかく、$j_{1,2,3}$さえわかれば、この操作から$\lambda$がわかるので、固有値$e^{i\lambda}$が分かるわけです。
実際にやってみる
ではqiskitでやってみます。
参考にするのは https://qiskit.org/textbook/ch-algorithms/quantum-phase-estimation.html
$2 \times 2$ユニタリ行列$U$としては、
U =
\begin{pmatrix}
1 & 0 \\
0 & e^{i\pi/4}
\end{pmatrix}
とします。
固有値は$e^{\lambda_{1}} = |1$, つまり $\lambda = 0$
すなわち $|j_{1}j_{2}j_{3} \rangle = |0 0 0 \rangle$ であって、
固有ベクトル $[1, 0]^{T} = |0 \rangle$,
固有値は$e^{\lambda_{2}} = e^{i\pi/4}$, つまり $\lambda = \pi/4$
すなわち $|j_{1}j_{2}j_{3} \rangle = |0 0 1 \rangle$ であって、
固有ベクトル $[0, 1]^{T} = |1 \rangle$
です。
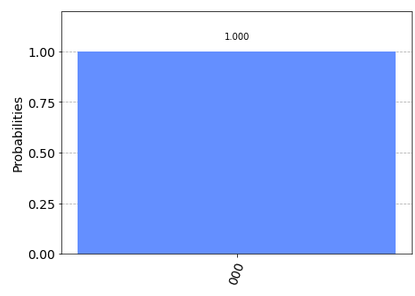
ではQPEに固有ベクトル $[1, 0]^{T} = |0 \rangle$を入れて、ちゃんと$|j_{1}j_{2}j_{3} \rangle = |0 0 0 \rangle$が出るのか見てみます。
pip install qiskit
pip install pylatexenc
# initialization
import matplotlib.pyplot as plt
import numpy as np
import math
# importing Qiskit
from qiskit import IBMQ, Aer
from qiskit import QuantumCircuit, ClassicalRegister, QuantumRegister, execute
# import basic plot tools
from qiskit.visualization import plot_histogram
# U = [1 0 ; 0 exp(pi/4)]
# eigen value is 2pi(0) for |0> , 2pi(0.001) for |1>
qpe = QuantumCircuit(4, 3) # 1 bit for eigen state and 3 bits for phase kick back
qpe.id(3) # 3rd bit becomes eigen state, |0>
for qubit in range(3):
qpe.h(qubit)
repetitions = 1
for counting_qubit in range(3):
for i in range(repetitions):
qpe.cu1(math.pi/4, counting_qubit, 3); # This is Controlled-U
repetitions *= 2
def qft_dagger(circ, n):
"""n-qubit QFTdagger the first n qubits in circ"""
# Don't forget the Swaps!
for qubit in range(n//2):
circ.swap(qubit, n-qubit-1)
for j in range(n):
for m in range(j):
circ.cu1(-math.pi/float(2**(j-m)), m, j)
circ.h(j)
qpe.barrier()
# Apply inverse QFT
qft_dagger(qpe, 3)
# Measure
qpe.barrier()
for n in range(3):
qpe.measure(n,n)
qpe.draw('mpl')
backend = Aer.get_backend('qasm_simulator')
shots = 2048
results = execute(qpe, backend=backend, shots=shots).result()
answer = results.get_counts()
plot_histogram(answer)
ちゃんと出ていますね!
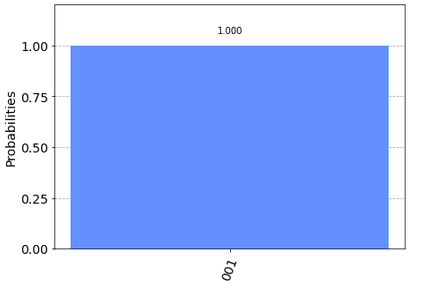
ではQPEに固有ベクトル $[0, 1]^{T} = |1 \rangle$を入れて、ちゃんと$|j_{1}j_{2}j_{3} \rangle = |0 0 1 \rangle$が出るのか見てみます。
以下のようにすればOKです。
qpe.x(3) # 3rd bit becomes eigen state, |1>
正解!
では、固有ベクトルとは限らない(つまり固有ベクトルが未知の状況)ものを入れてみます。
この場合、固有値は重ね合わせで出てくるはずです。
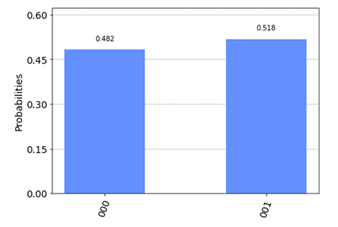
簡単のために、$\frac{1}{\sqrt(2)}(|0\rangle + |1\rangle)$を入れてみます。
qpe.h(3) # 3rd bit becomes unknown state
でOKですね。
確かに固有値が重ね合わせで出てきていますね。
でもこれでは「どっちの固有ベクトルに対応する固有値なのか」がわかりません。
これをみるためには、$|\psi \rangle$のQPE出力も測ってやればいいです。
(これが出来るのは、固有ベクトルがたまたまZ基底での固有ベクトルになっていたからです。
一般には量子トモグラフィとかをしないと、状態ベクトルそのものの推定はできないかと。)
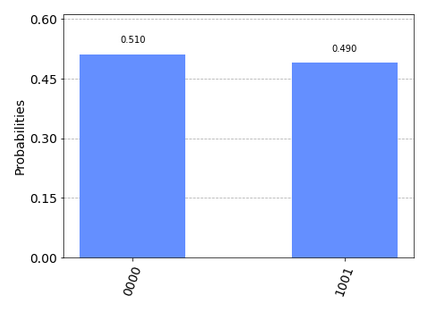
こいつは対応する固有ベクトルに収束しています。実際やってみると、
となります。第一bitが固有ベクトルを示しています。ちゃんと固有ベクトルと固有値がペアでわかりますね。
実機実行
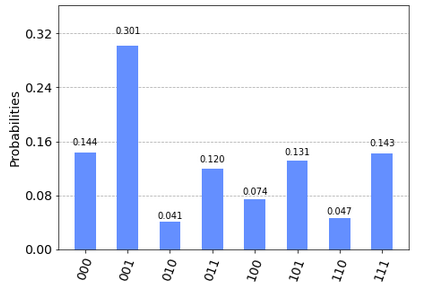
実機でもやってみます。ibmq_santiago使います。入力は $|1 \rangle $とします。001が正解です。
あらら、これは厳しいですね。
確かに最大確率を取っているのは001ですが、確率100%で出てほしいことを考えると、残念です。
うまく推定するには、補助量子ビットを減らしたり(反復QPE)、回路分割したり(MLQPE)、色々工夫しないとだめそうです。
結論
QPEの動作がわかった。でも工夫しないと実機では厳しい。