VBAで緯度経度から距離を計算する。

はじめに

　緯度経度をもとに２点間の距離（※メートル）を求めるものです。
　今回紹介するものは、以下の要素で計算しています。
　・GRS80（長半径：6378136.6、扁平率：1/298.257222101）
　・Lambert_Andoyerの公式

Option Explicit

Global Const a As Double = 6378136.6 ' 長半径
Global Const f As Double = 1 / 298.257222101 ' 扁平率

'//////////////////////////////////////////////////////////////////////////////////
'// ArcCos計算用関数                                                             //
'////////////////////////////////////////////////////////////////////////////////// 
Function arcCos(x As Double)
  If x <= -1 Then
    arcCos = 4 * Atn(1)
  ElseIf x >= 1 Then
    arcCos = 0
  Else
    arcCos = Atn(-x / Sqr(-x * x + 1)) + 2 * Atn(1)
  End If
End Function

'//////////////////////////////////////////////////////////////////////////////////
'//　距離計算関数　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　  //
'////////////////////////////////////////////////////////////////////////////////// 
Function Lambert_Andoyer(t1 As Double, g1 As Double, t2 As Double, g2 As Double)
  Dim U1, U2
  Dim x As Double, dP As Double
  
  If t1 - t2 = 0 And g1 - g2 = 0 Then
     Lambert_Andoyer = 0
  Else
     t1 = t1 * 4 * Atn(1) / 180
     t2 = t2 * 4 * Atn(1) / 180
     g1 = g1 * 4 * Atn(1) / 180
     g2 = g2 * 4 * Atn(1) / 180
  
     U1 = Atn((1 - f) * Tan(t1))
     U2 = Atn((1 - f) * Tan(t2))
     x = arcCos(Sin(U1) * Sin(U2) + Cos(U1) * Cos(U2) * Cos(g1 - g2))
     if x = 0 then
        Lambert_Andoyer = 0
     else
        dP = f / 8 * ((Sin(x) - x) * (Sin(U1) + Sin(U2)) ^ 2 / Cos(x / 2) ^ 2 - (Sin(x) + x) * (Sin(U1) - Sin(U2)) ^ 2 / Sin(x / 2) ^ 2)
        Lambert_Andoyer = a * (x + dP)
     end
  End If
End Function

計算する場合、以下のようにデータを渡す
Lambert_Andoyer(緯度１,経度１, 緯度２, 経度２)
※引数は10進数で渡す必要があります。
　351236N→ 35.21
　351236S→-35.21
　1351236E→ 135.21
　1351236W→-135.21

Sub test()
    MsgBox (Lambert_Andoyer(35, 135, 35, 136) & "m")
End Sub

さいごに

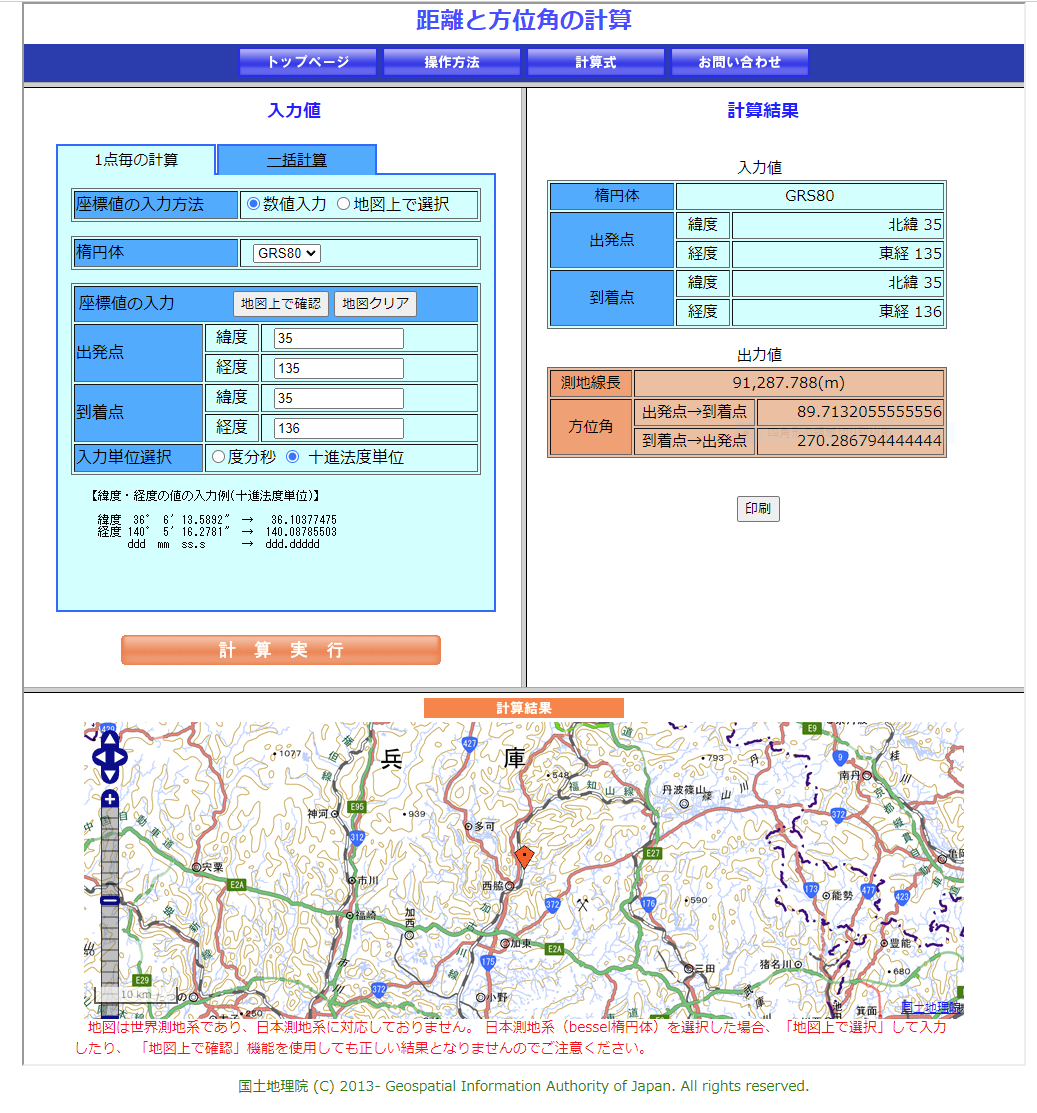
国土地理院での計測値は下図の通り。
VBAでの計算値は91287.7827298676mなので、6mm程度の誤差があった。

参　考

地図投影法――地理空間情報の技法　著者：政春　尋志（国土地理院基本図情報部長）