LoginSignup
206
120

More than 3 years have passed since last update.

@notargsin株式会社 バーチャルキャスト

UnityEngine.Meshの内部構造解説

Last updated at Posted at 2016-12-10

自己紹介

cat2.png

のたぐす(@notargs)
- シェーダー書いたりUI作ったりしてます

LGTM Shaders

LGTM
LGTM

よく聞く話

  • 「Meshってデザイナーが弄るものでしょ？」
  • 「Meshってゲームエンジンに任せるものでしょ？？」
  • 「Meshを動的に切断したいけど全然イメージつかない」

今回の話の概要

  • Mesh怖くないよ！！
  • UnityのMeshを使いこなせばプログラマーでもモデリングできる！という話

SnapCrab_NoName_2016-12-6_11-18-34_No-00.png

内容

  • Meshの内部構造について解説
  • スクリプトからMeshを組み立てる方法
  • 応用例

どういうときに役立つの？

  • 幾何形体など、スクリプトで生成した方が早いとき
  • 同じ物体を等間隔に並べたいとき
  • SetPassCall削減
  • モデリングツールを持っていないとき

基礎編: Meshが持つ情報

Vertex(頂点位置)

  • 各頂点の位置
  • 内部はただのVector3型の配列

temp.png

Normal(法線)

  • 各頂点についての面の向き
  • ライティングや衝突判定などに活用される
  • Vertexと同じ長さのVector3型配列

temp.png

Tangent(接線) ＆ Binormal(従法線)

  • 各頂点についてのNormalに対して直交なベクトル
  • ライティング時にNormalを補助する形で使われる
  • 法線マップテクスチャを張るときなどに必須

temp.png

UV1 ~ UV4(テクスチャ座標)

  • 頂点ごとのテクスチャ位置
  • 1つの頂点につき4個まで持つことができる
  • 2個目以降は複数枚のテクスチャを重ねたい時などに活用

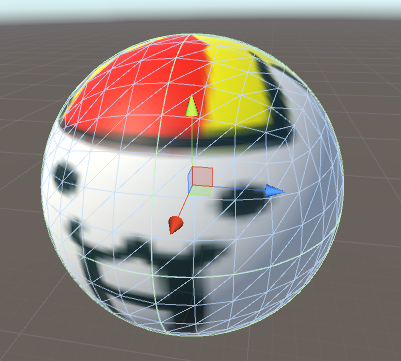
SnapCrab_NoName_2016-12-6_10-49-16_No-00.png

Color(頂点カラー)

  • 頂点ごとの色情報
  • Standardシェーダーでは出力されない点は注意
  • 下の画像はSpriteシェーダー

SnapCrab_NoName_2016-12-6_10-56-51_No-00.png

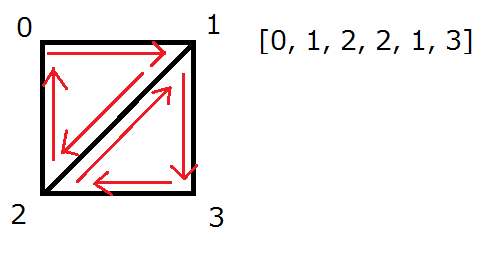
Index(頂点インデックス)

  • ポリゴンを定義する
  • 配列上での頂点のインデックスを3つずつ並べて指定
  • 時計回りor反時計回りでポリゴンの裏or表が決まる

無題.png

Bounds(領域)

  • Mesh全体を覆う長方形
  • カメラから見た内外判定などに使われている

SnapCrab_NoName_2016-12-6_11-18-34_No-00.png

応用編1: Quadを自作してみる

  • 4つの頂点を定義
  • 2つのポリゴンを定義

無題.png

MeshCreator.cs
void Start()
{
    // Meshを作成
    var mesh = new Mesh();

    // 頂点を設定
    mesh.vertices = (
        from y in new[] {-1, 1}
        from x in new[] {-1, 1}
        select new Vector3(x, y, 0)).ToArray();

    // 頂点インデックスを設定
    mesh.triangles = new[] {0, 1, 2, 2, 1, 3};

    // 領域と法線を自動で再計算する
    mesh.RecalculateBounds();
    mesh.RecalculateNormals();

    // MeshFilterに設定
    GetComponent<MeshFilter>().mesh = mesh;
}

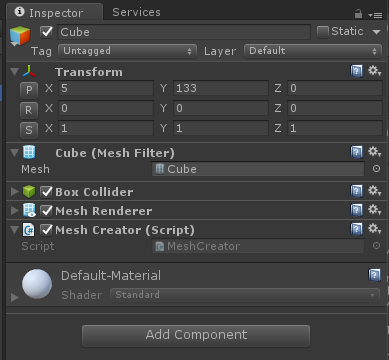
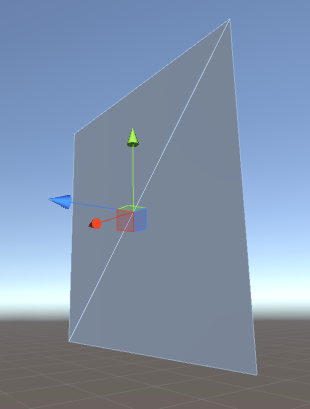
MeshFilterとMeshRendererを持ったGameObjectを作って先ほどのスクリプトをアタッチ

SnapCrab_NoName_2016-12-6_11-23-11_No-00.png

実行するとQuadが表示される

SnapCrab_NoName_2016-12-6_11-24-12_No-00.png

大量に配置することでパーティクルにも

無題7.png

応用編2: ペンパイナッポーアッポーペンを自作してみる

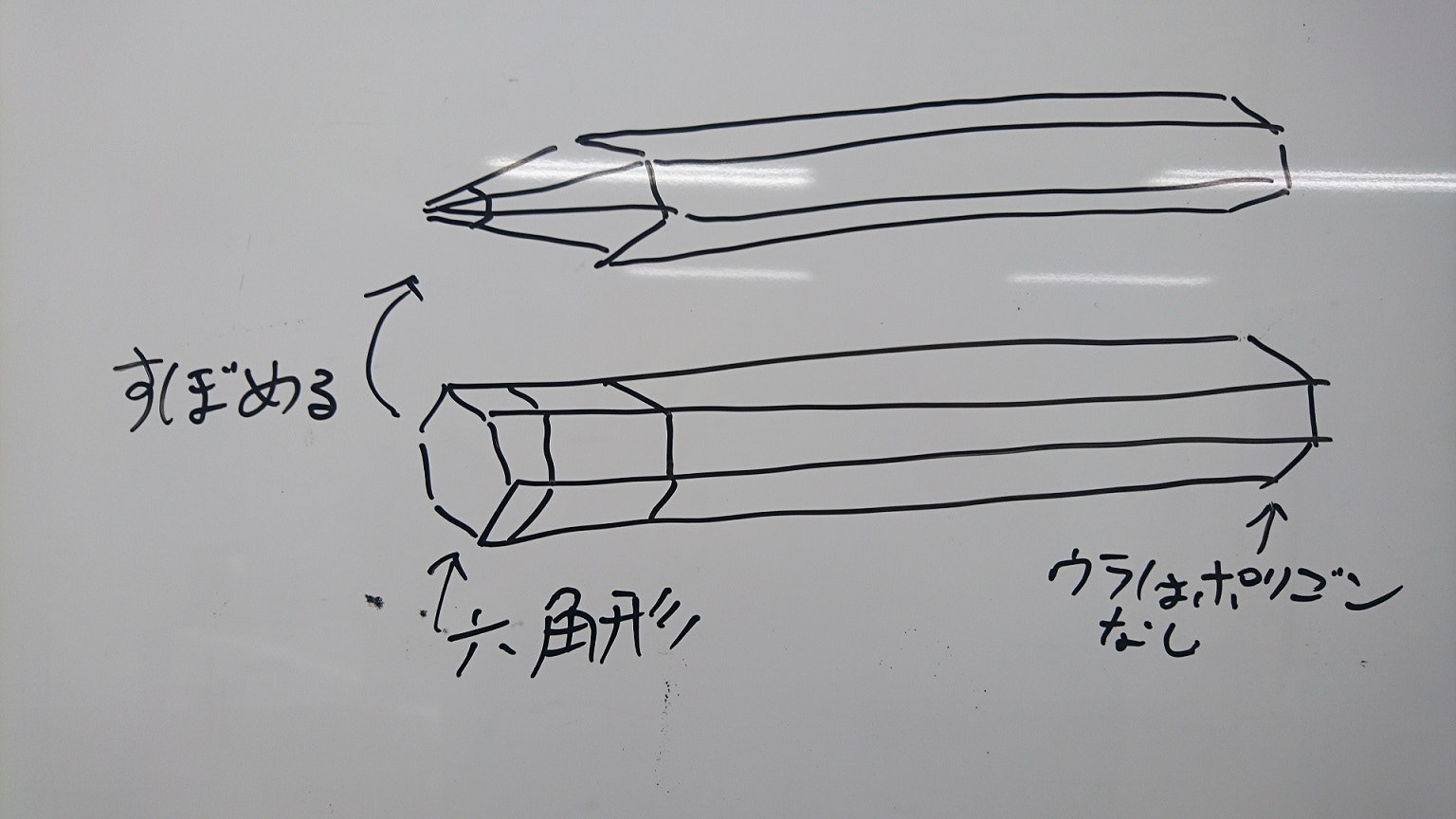
ペンの設計

pen.jpeg

ペンの実装

void Pen(Matrix4x4 world)
{
    var indexOffset = vertices.Count;

    const int ySize = 11;
    const int xSize = 6;
    vertices.AddRange(
        from y in Enumerable.Range(0, ySize)
        from x in Enumerable.Range(0, xSize)
        from y2 in new[] { -0.5f, 0.5f }.Select(v => v + y - ySize / 2.0f)
        from x2 in new[] { -0.5f, 0.5f }.Select(v => v + x - xSize / 2.0f)
        select world.MultiplyPoint(Quaternion.AngleAxis(x2 / xSize * 360.0f, Vector3.up) * Vector3.forward
        * Mathf.Clamp01(y2 + ySize / 2) * 0.05f + Vector3.up * y2 / ySize * 2.0f)
    );

    colors.AddRange(Enumerable.Range(0, vertices.Count - indexOffset).Select(_ => new Color(0.2f, 0.1f, 0.1f)));

    foreach (var x in Enumerable.Range(0, (vertices.Count - indexOffset) / 4))
    {
        triangles.AddRange(new []
        {
            0, 1, 2,
            2, 1, 3,
        }.Select(i => indexOffset + x * 4 + i));
    }
}

SnapCrab_NoName_2016-12-9_19-43-49_No-00.png

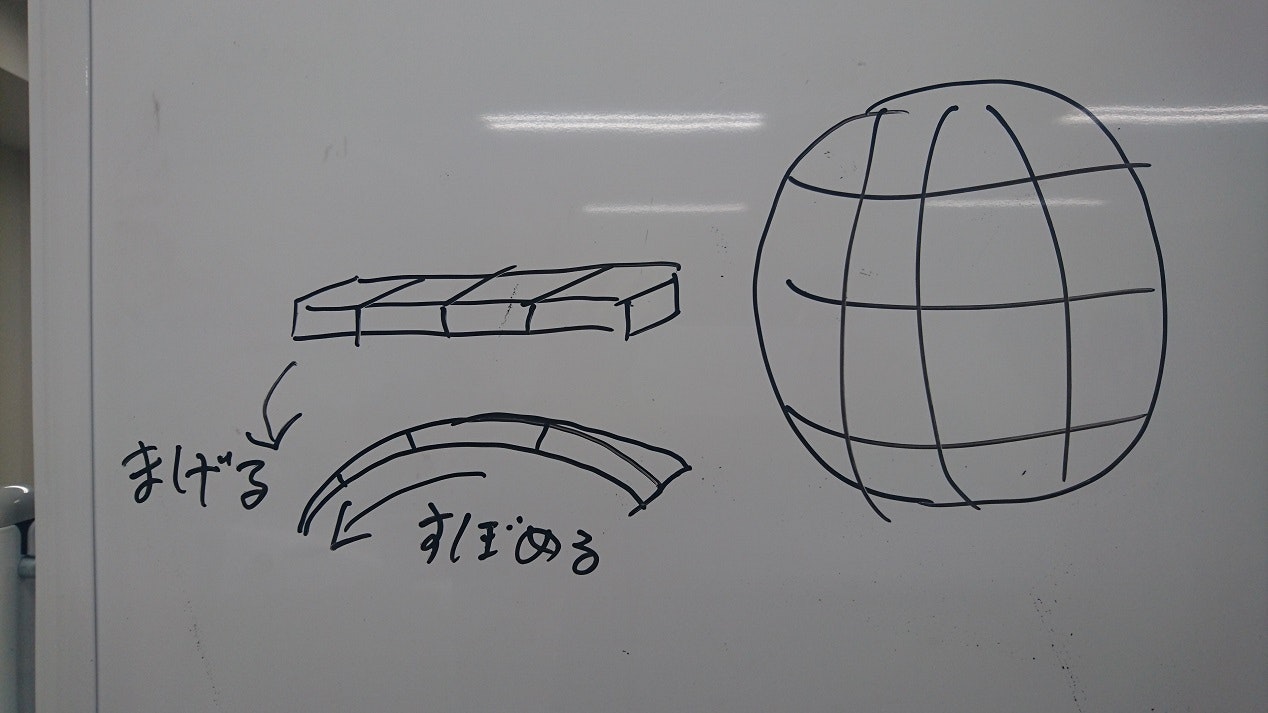
パイナッポーの設計

pineapple.jpeg

パイナッポーの葉っぱの実装

void PineappleGlass(Matrix4x4 world)
{
    var indexOffset = vertices.Count;

    const int ySize = 7;
    const int xSize = 4;
    vertices.AddRange(
        from y in Enumerable.Range(0, ySize)
        from x in Enumerable.Range(0, xSize)
        from y2 in new[] { 0, 1 }.Select(v => v + y)
        from x2 in new[] { 0, 1 }.Select(v => v + x - xSize / 2.0f)
        from vec in new [] { Quaternion.AngleAxis(x2 / xSize * 360.0f + 45, Vector3.up) * new Vector3(0, y2, 1) }
        select world.MultiplyPoint(new Vector3(vec.x * (1 - vec.y / ySize), vec.y * 0.5f, vec.z * 0.3f + Mathf.Pow(vec.y / ySize * 2.0f, 2.0f)))
    );

    colors.AddRange(Enumerable.Range(0, vertices.Count - indexOffset).Select(_ => new Color(0.2f, 0.6f, 0.2f)));

    foreach (var x in Enumerable.Range(0, (vertices.Count - indexOffset) / 4))
    {
        triangles.AddRange(new[]
        {
            0, 1, 2,
            2, 1, 3,
        }.Select(i => indexOffset + x * 4 + i));
    }
}

パイナッポーの実装

void Pineapple(Matrix4x4 world)
{
    var indexOffset = vertices.Count;

    const int ySize = 11;
    const int xSize = 20;
    vertices.AddRange(
        from y in Enumerable.Range(0, ySize)
        from x in Enumerable.Range(0, xSize)
        from y2 in new[] { 0, 1 }.Select(v => v + y - ySize / 2.0f)
        from x2 in new[] { 0, 1 }.Select(v => v + x - xSize / 2.0f)
        select world.MultiplyPoint(Quaternion.AngleAxis(x2 / xSize * 360.0f, Vector3.up)
        * new Vector3(0, Mathf.Sin(y2 / ySize * Mathf.PI) * 1.3f, Mathf.Cos(y2 / ySize * Mathf.PI)) * Mathf.Cos(y2 * 0.1f))
    );

    colors.AddRange(Enumerable.Range(0, vertices.Count - indexOffset).Select(_ => new Color(0.6f, 0.6f, 0.2f)));

    foreach (var x in Enumerable.Range(0, (vertices.Count - indexOffset) / 4))
    {
        triangles.AddRange(new []
        {
            0, 1, 2,
            2, 1, 3,
        }.Select(i => indexOffset + x * 4 + i));
    }

    for (var i = 0; i < 30; ++i)
    {
        PineappleGlass(world * Matrix4x4.TRS(Vector3.up * (1 + Random.Range(0.0f, 1.0f)), Quaternion.AngleAxis(Random.Range(0, 360), Vector3.up), Vector3.one * 0.3f));
    }
}

パイナッポー

SnapCrab_NoName_2016-12-10_14-3-18_No-00.png

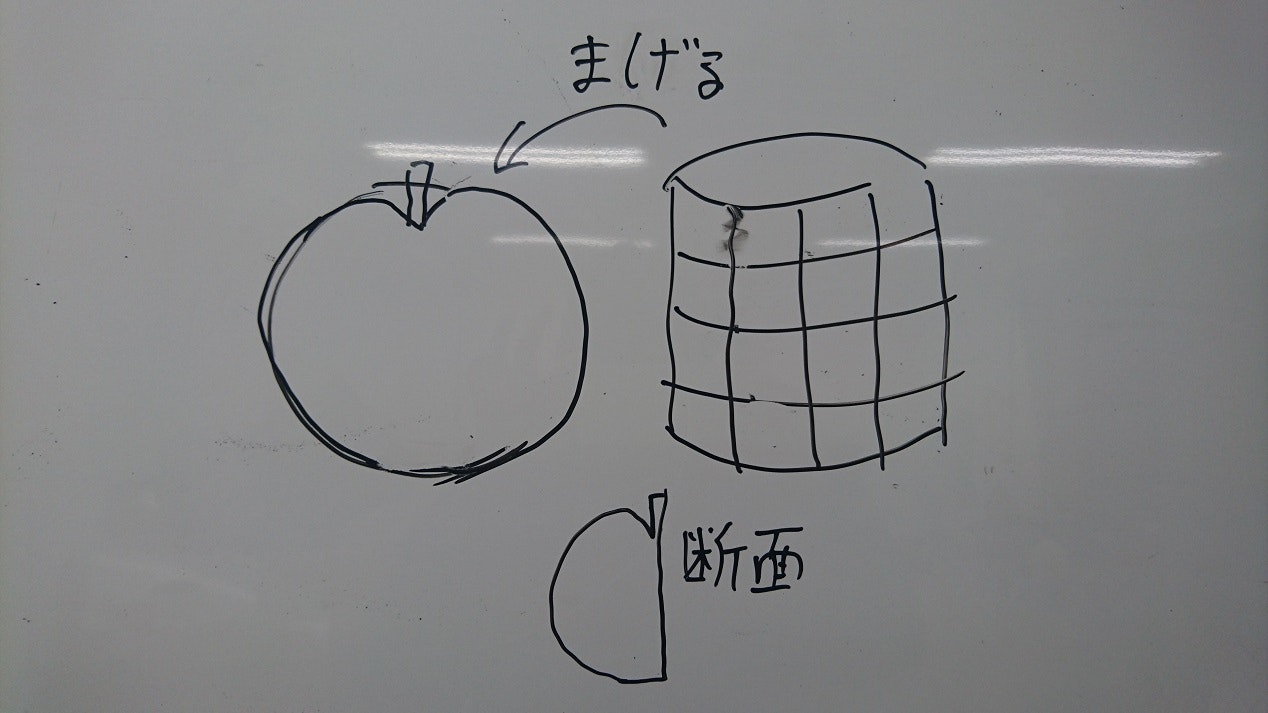
アップルの設計

apple.jpeg

アップルの試作

造形が難しいのでGLSL Sandboxで試作
SnapCrab_NoName_2016-12-9_8-53-37_No-00.png

アップルの実装


static Vector3 ProtApple(float t)
{
    t += 0.5f;
    var p = new Vector2(Mathf.Sin(t * Mathf.PI), Mathf.Cos(t * Mathf.PI)) * 0.3f * (Mathf.Pow(t, 0.8f) * Mathf.Pow(1.0f - t, 0.1f) + 0.3f);
    if (t < 0.02f)
    {
        p.y = 0.2f;
    }
    return p;
}

void Apple(Matrix4x4 world)
{
    var indexOffset = vertices.Count;

    const int ySize = 80;
    const int xSize = 30;
    vertices.AddRange(
        from y in Enumerable.Range(0, ySize)
        from x in Enumerable.Range(0, xSize)
        from y2 in new[] { 0, 1 }.Select(v => v + y - ySize / 2.0f)
        from x2 in new[] { 0, 1 }.Select(v => v + x - xSize / 2.0f)
        select world.MultiplyPoint(Quaternion.AngleAxis(x2 / xSize * 360.0f, Vector3.up) * ProtApple(y2 / ySize))
    );

    colors.AddRange(Enumerable.Range(0, vertices.Count - indexOffset).Select(_ => new Color(0.5f, 0.1f, 0.1f)));

    foreach (var x in Enumerable.Range(0, (vertices.Count - indexOffset) / 4))
    {
        triangles.AddRange(new[]
        {
            0, 2, 1,
            1, 2, 3,
        }.Select(i => indexOffset + x * 4 + i));
    }
}

アップルの動作

SnapCrab_NoName_2016-12-9_19-47-31_No-00.png

全てを結合してメッシュを作成

Mesh mesh;

List<Vector3> vertices;
List<Color> colors;
List<int> triangles;

void Start ()
{
    mesh = new Mesh();

    vertices = new List<Vector3>();
    colors = new List<Color>();
    triangles = new List<int>();

    Pen(Matrix4x4.TRS(new Vector3(-1.75f, 0, 0), Quaternion.AngleAxis(90, Vector3.forward), Vector3.one * 0.7f));
    Pineapple(Matrix4x4.TRS(new Vector3(-0.5f, 0, 0), Quaternion.identity, Vector3.one * 0.7f));
    Apple(Matrix4x4.TRS(new Vector3(0.5f, 0, 0), Quaternion.identity, Vector3.one * 1.3f));
    Pen(Matrix4x4.TRS(new Vector3(1.35f, 0, 0), Quaternion.AngleAxis(-90, Vector3.forward), Vector3.one * 0.7f));

    mesh.SetVertices(vertices);
    mesh.SetTriangles(triangles, 0);
    mesh.SetColors(colors);
    mesh.RecalculateNormals();
    mesh.RecalculateBounds();

    GetComponent<MeshFilter>().mesh = mesh;
}

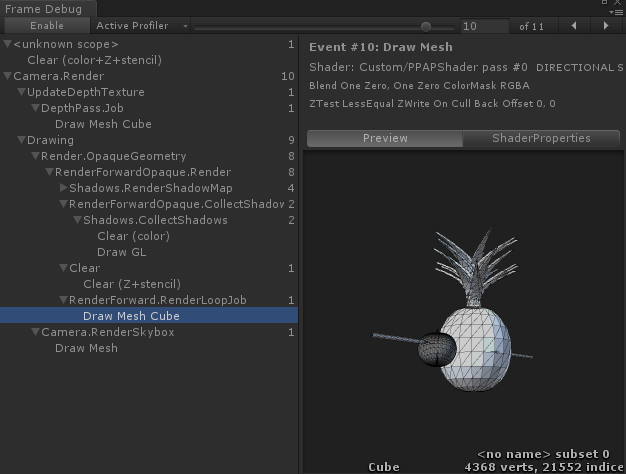
動作

SnapCrab_NoName_2016-12-9_19-40-58_No-00.png
glsl.gif

一つのメッシュなのでSetPassCallも少ない！

SnapCrab_NoName_2016-12-9_19-41-46_No-00.png

自前でメッシュを作ってるので、シェーダーの自由度も高い！

glsl2.gif

まとめ

  • Mayaで作った方が早い :innocent:
  • シェーダー沼はいいぞ！！
206
120
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
206
120